StreamRL: Scalable, Heterogeneous, and Elastic RL for LLMs with Disaggregated Stream Generation

Reinforcement learning (RL) has become the core post-training technique for large language models (LLMs). RL for LLMs involves two stages: generation and training. The LLM first generates samples online, which are then used to derive rewards for training. The conventional view holds that the colocated architecture, where the two stages share resources via temporal multiplexing, outperforms the disaggregated architecture, in which dedicated resources are assigned to each stage. However, in real-world deployments, we observe that the colocated architecture suffers from resource coupling, where the two stages are constrained to use the same resources. This coupling compromises the scalability and cost-efficiency of colocated RL in large-scale training. In contrast, the disaggregated architecture allows for flexible resource allocation, supports heterogeneous training setups, and facilitates cross-datacenter deployment. StreamRL is designed with disaggregation from first principles and fully unlocks its potential by addressing two types of performance bottlenecks in existing disaggregated RL frameworks: pipeline bubbles, caused by stage dependencies, and skewness bubbles, resulting from long-tail output length distributions. To address pipeline bubbles, StreamRL breaks the traditional stage boundary in synchronous RL algorithms through stream generation and achieves full overlapping in asynchronous RL. To address skewness bubbles, StreamRL employs an output-length ranker model to identify long-tail samples and reduces generation time via skewness-aware dispatching and scheduling. Experiments show that StreamRL improves throughput by up to 2.66x compared to existing state-of-the-art systems, and improves cost-effectiveness by up to 1.33x in a heterogeneous, cross-datacenter setting.

REFINE: Inversion-Free Backdoor Defense via Model Reprogramming

Backdoor attacks on deep neural networks (DNNs) have emerged as a significant security threat, allowing adversaries to implant hidden malicious behaviors during the model training phase. Pre-processing-based defense, which is one of the most important defense paradigms, typically focuses on input transformations or backdoor trigger inversion (BTI) to deactivate or eliminate embedded backdoor triggers during the inference process. However, these methods suffer from inherent limitations: transformation-based defenses often fail to balance model utility and defense performance, while BTI-based defenses struggle to accurately reconstruct trigger patterns without prior knowledge. In this paper, we propose REFINE, an inversion-free backdoor defense method based on model reprogramming. REFINE consists of two key components: \textbf{(1)} an input transformation module that disrupts both benign and backdoor patterns, generating new benign features; and \textbf{(2)} an output remapping module that redefines the model's output domain to guide the input transformations effectively. By further integrating supervised contrastive loss, REFINE enhances the defense capabilities while maintaining model utility. Extensive experiments on various benchmark datasets demonstrate the effectiveness of our REFINE and its resistance to potential adaptive attacks.

PersonaMath: Enhancing Math Reasoning through Persona-Driven Data Augmentation

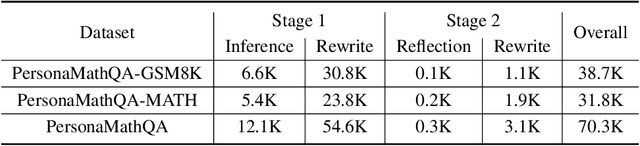
While closed-source Large Language Models (LLMs) demonstrate strong mathematical problem-solving abilities, open-source models continue to struggle with such tasks. To bridge this gap, we propose a data augmentation approach and introduce PersonaMathQA, a dataset derived from MATH and GSM8K, on which we train the PersonaMath models. Our approach consists of two stages: the first stage is learning from Persona Diversification, and the second stage is learning from Reflection. In the first stage, we regenerate detailed chain-of-thought (CoT) solutions as instructions using a closed-source LLM and introduce a novel persona-driven data augmentation technique to enhance the dataset's quantity and diversity. In the second stage, we incorporate reflection to fully leverage more challenging and valuable questions. Evaluation of our PersonaMath models on MATH and GSM8K reveals that the PersonaMath-7B model (based on LLaMA-2-7B) achieves an accuracy of 24.2% on MATH and 68.7% on GSM8K, surpassing all baseline methods and achieving state-of-the-art performance. Notably, our dataset contains only 70.3K data points-merely 17.8% of MetaMathQA and 27% of MathInstruct-yet our model outperforms these baselines, demonstrating the high quality and diversity of our dataset, which enables more efficient model training. We open-source the PersonaMathQA dataset, PersonaMath models, and our code for public usage.

Towards the Better Ranking Consistency: A Multi-task Learning Framework for Early Stage Ads Ranking

Dividing ads ranking system into retrieval, early, and final stages is a common practice in large scale ads recommendation to balance the efficiency and accuracy. The early stage ranking often uses efficient models to generate candidates out of a set of retrieved ads. The candidates are then fed into a more computationally intensive but accurate final stage ranking system to produce the final ads recommendation. As the early and final stage ranking use different features and model architectures because of system constraints, a serious ranking consistency issue arises where the early stage has a low ads recall, i.e., top ads in the final stage are ranked low in the early stage. In order to pass better ads from the early to the final stage ranking, we propose a multi-task learning framework for early stage ranking to capture multiple final stage ranking components (i.e. ads clicks and ads quality events) and their task relations. With our multi-task learning framework, we can not only achieve serving cost saving from the model consolidation, but also improve the ads recall and ranking consistency. In the online A/B testing, our framework achieves significantly higher click-through rate (CTR), conversion rate (CVR), total value and better ads-quality (e.g. reduced ads cross-out rate) in a large scale industrial ads ranking system.

Boxhead: A Dataset for Learning Hierarchical Representations

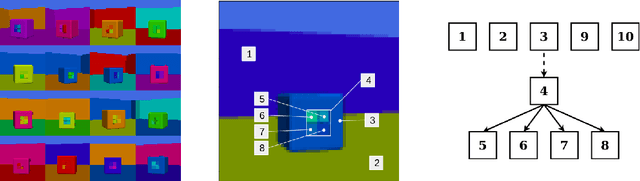
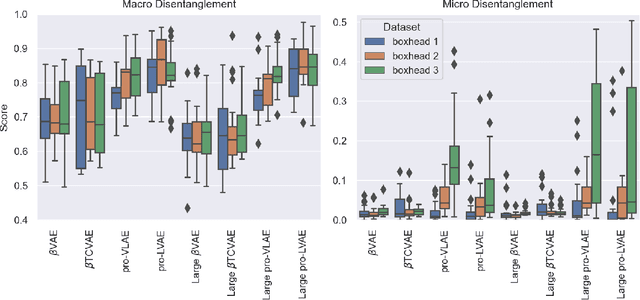
Disentanglement is hypothesized to be beneficial towards a number of downstream tasks. However, a common assumption in learning disentangled representations is that the data generative factors are statistically independent. As current methods are almost solely evaluated on toy datasets where this ideal assumption holds, we investigate their performance in hierarchical settings, a relevant feature of real-world data. In this work, we introduce Boxhead, a dataset with hierarchically structured ground-truth generative factors. We use this novel dataset to evaluate the performance of state-of-the-art autoencoder-based disentanglement models and observe that hierarchical models generally outperform single-layer VAEs in terms of disentanglement of hierarchically arranged factors.

MEBOW: Monocular Estimation of Body Orientation In the Wild

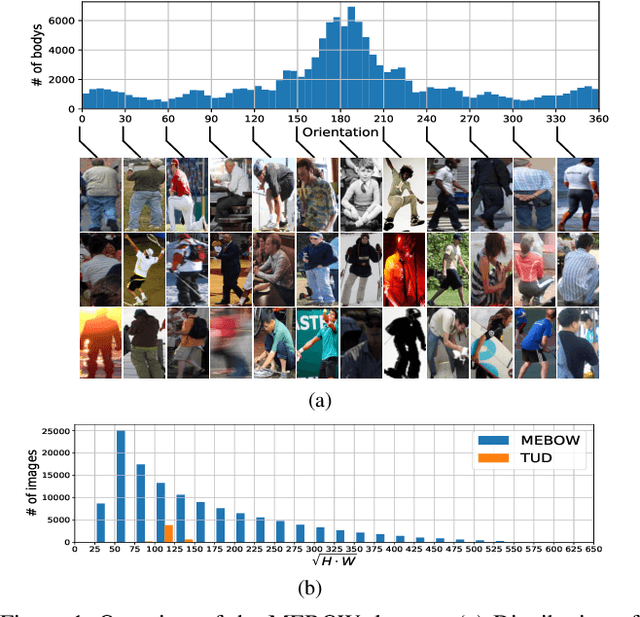
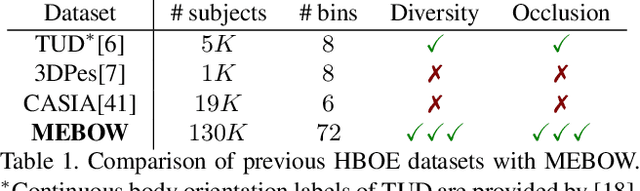
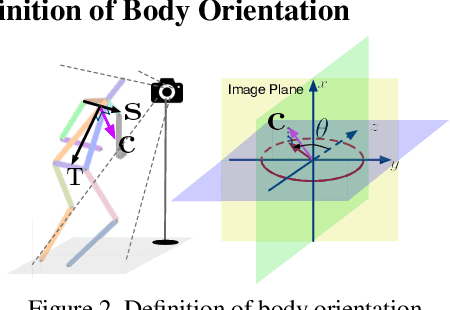
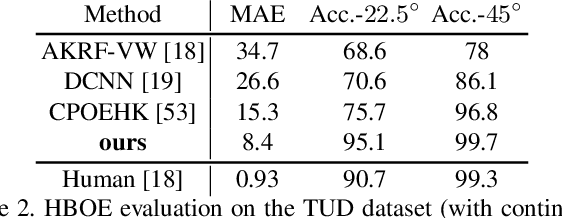
Body orientation estimation provides crucial visual cues in many applications, including robotics and autonomous driving. It is particularly desirable when 3-D pose estimation is difficult to infer due to poor image resolution, occlusion or indistinguishable body parts. We present COCO-MEBOW (Monocular Estimation of Body Orientation in the Wild), a new large-scale dataset for orientation estimation from a single in-the-wild image. The body-orientation labels for around 130K human bodies within 55K images from the COCO dataset have been collected using an efficient and high-precision annotation pipeline. We also validated the benefits of the dataset. First, we show that our dataset can substantially improve the performance and the robustness of a human body orientation estimation model, the development of which was previously limited by the scale and diversity of the available training data. Additionally, we present a novel triple-source solution for 3-D human pose estimation, where 3-D pose labels, 2-D pose labels, and our body-orientation labels are all used in joint training. Our model significantly outperforms state-of-the-art dual-source solutions for monocular 3-D human pose estimation, where training only uses 3-D pose labels and 2-D pose labels. This substantiates an important advantage of MEBOW for 3-D human pose estimation, which is particularly appealing because the per-instance labeling cost for body orientations is far less than that for 3-D poses. The work demonstrates high potential of MEBOW in addressing real-world challenges involving understanding human behaviors. Further information of this work is available at https://chenyanwu.github.io/MEBOW/.

Detecting Comma-shaped Clouds for Severe Weather Forecasting using Shape and Motion

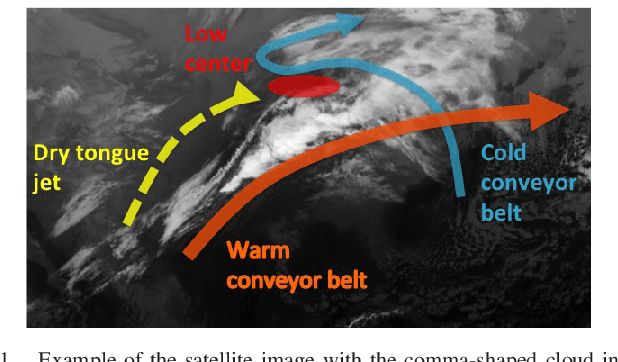
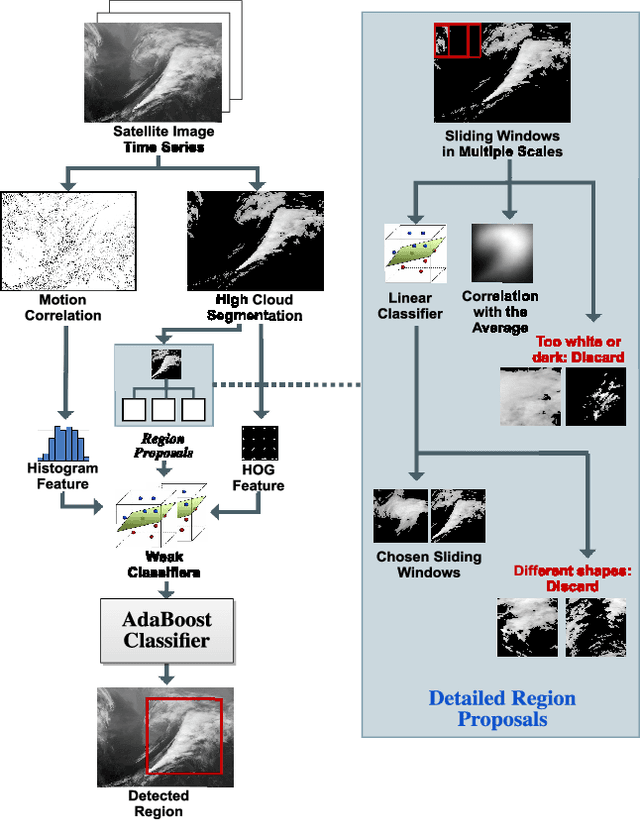
Meteorologists use shapes and movements of clouds in satellite images as indicators of several major types of severe storms. Satellite imaginary data are in increasingly higher resolution, both spatially and temporally, making it impossible for humans to fully leverage the data in their forecast. Automatic satellite imagery analysis methods that can find storm-related cloud patterns as soon as they are detectable are in demand. We propose a machine learning and pattern recognition based approach to detect "comma-shaped" clouds in satellite images, which are specific cloud distribution patterns strongly associated with the cyclone formulation. In order to detect regions with the targeted movement patterns, our method is trained on manually annotated cloud examples represented by both shape and motion-sensitive features. Sliding windows in different scales are used to ensure that dense clouds will be captured, and we implement effective selection rules to shrink the region of interest among these sliding windows. Finally, we evaluate the method on a hold-out annotated comma-shaped cloud dataset and cross-match the results with recorded storm events in the severe weather database. The validated utility and accuracy of our method suggest a high potential for assisting meteorologists in weather forecasting.

Aggregated Wasserstein Metric and State Registration for Hidden Markov Models

We propose a framework, named Aggregated Wasserstein, for computing a dissimilarity measure or distance between two Hidden Markov Models with state conditional distributions being Gaussian. For such HMMs, the marginal distribution at any time position follows a Gaussian mixture distribution, a fact exploited to softly match, aka register, the states in two HMMs. We refer to such HMMs as Gaussian mixture model-HMM (GMM-HMM). The registration of states is inspired by the intrinsic relationship of optimal transport and the Wasserstein metric between distributions. Specifically, the components of the marginal GMMs are matched by solving an optimal transport problem where the cost between components is the Wasserstein metric for Gaussian distributions. The solution of the optimization problem is a fast approximation to the Wasserstein metric between two GMMs. The new Aggregated Wasserstein distance is a semi-metric and can be computed without generating Monte Carlo samples. It is invariant to relabeling or permutation of states. The distance is defined meaningfully even for two HMMs that are estimated from data of different dimensionality, a situation that can arise due to missing variables. This distance quantifies the dissimilarity of GMM-HMMs by measuring both the difference between the two marginal GMMs and that between the two transition matrices. Our new distance is tested on tasks of retrieval, classification, and t-SNE visualization of time series. Experiments on both synthetic and real data have demonstrated its advantages in terms of accuracy as well as efficiency in comparison with existing distances based on the Kullback-Leibler divergence.

A Distance for HMMs based on Aggregated Wasserstein Metric and State Registration

We propose a framework, named Aggregated Wasserstein, for computing a dissimilarity measure or distance between two Hidden Markov Models with state conditional distributions being Gaussian. For such HMMs, the marginal distribution at any time spot follows a Gaussian mixture distribution, a fact exploited to softly match, aka register, the states in two HMMs. We refer to such HMMs as Gaussian mixture model-HMM (GMM-HMM). The registration of states is inspired by the intrinsic relationship of optimal transport and the Wasserstein metric between distributions. Specifically, the components of the marginal GMMs are matched by solving an optimal transport problem where the cost between components is the Wasserstein metric for Gaussian distributions. The solution of the optimization problem is a fast approximation to the Wasserstein metric between two GMMs. The new Aggregated Wasserstein distance is a semi-metric and can be computed without generating Monte Carlo samples. It is invariant to relabeling or permutation of the states. This distance quantifies the dissimilarity of GMM-HMMs by measuring both the difference between the two marginal GMMs and the difference between the two transition matrices. Our new distance is tested on the tasks of retrieval and classification of time series. Experiments on both synthetic data and real data have demonstrated its advantages in terms of accuracy as well as efficiency in comparison with existing distances based on the Kullback-Leibler divergence.