Muse: Towards Reproducible Long-Form Song Generation with Fine-Grained Style Control

Recent commercial systems such as Suno demonstrate strong capabilities in long-form song generation, while academic research remains largely non-reproducible due to the lack of publicly available training data, hindering fair comparison and progress. To this end, we release a fully open-source system for long-form song generation with fine-grained style conditioning, including a licensed synthetic dataset, training and evaluation pipelines, and Muse, an easy-to-deploy song generation model. The dataset consists of 116k fully licensed synthetic songs with automatically generated lyrics and style descriptions paired with audio synthesized by SunoV5. We train Muse via single-stage supervised finetuning of a Qwen-based language model extended with discrete audio tokens using MuCodec, without task-specific losses, auxiliary objectives, or additional architectural components. Our evaluations find that although Muse is trained with a modest data scale and model size, it achieves competitive performance on phoneme error rate, text--music style similarity, and audio aesthetic quality, while enabling controllable segment-level generation across different musical structures. All data, model weights, and training and evaluation pipelines will be publicly released, paving the way for continued progress in controllable long-form song generation research. The project repository is available at https://github.com/yuhui1038/Muse.

FADTI: Fourier and Attention Driven Diffusion for Multivariate Time Series Imputation

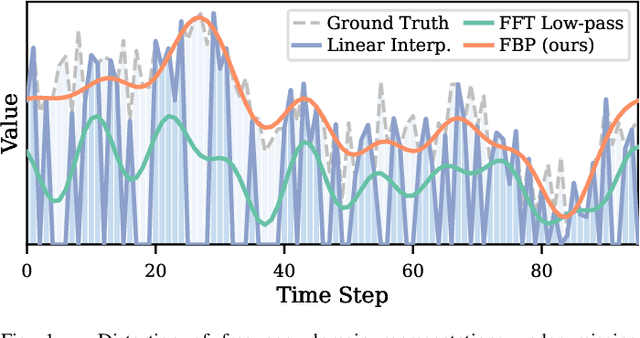
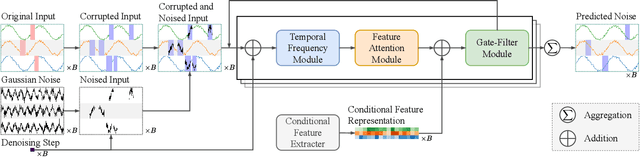
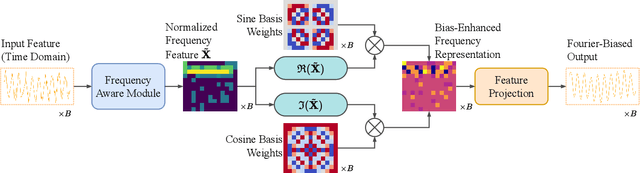
Multivariate time series imputation is fundamental in applications such as healthcare, traffic forecasting, and biological modeling, where sensor failures and irregular sampling lead to pervasive missing values. However, existing Transformer- and diffusion-based models lack explicit inductive biases and frequency awareness, limiting their generalization under structured missing patterns and distribution shifts. We propose FADTI, a diffusion-based framework that injects frequency-informed feature modulation via a learnable Fourier Bias Projection (FBP) module and combines it with temporal modeling through self-attention and gated convolution. FBP supports multiple spectral bases, enabling adaptive encoding of both stationary and non-stationary patterns. This design injects frequency-domain inductive bias into the generative imputation process. Experiments on multiple benchmarks, including a newly introduced biological time series dataset, show that FADTI consistently outperforms state-of-the-art methods, particularly under high missing rates. Code is available at https://anonymous.4open.science/r/TimeSeriesImputation-52BF

OpenPros: A Large-Scale Dataset for Limited View Prostate Ultrasound Computed Tomography

Prostate cancer is one of the most common and lethal cancers among men, making its early detection critically important. Although ultrasound imaging offers greater accessibility and cost-effectiveness compared to MRI, traditional transrectal ultrasound methods suffer from low sensitivity, especially in detecting anteriorly located tumors. Ultrasound computed tomography provides quantitative tissue characterization, but its clinical implementation faces significant challenges, particularly under anatomically constrained limited-angle acquisition conditions specific to prostate imaging. To address these unmet needs, we introduce OpenPros, the first large-scale benchmark dataset explicitly developed for limited-view prostate USCT. Our dataset includes over 280,000 paired samples of realistic 2D speed-of-sound (SOS) phantoms and corresponding ultrasound full-waveform data, generated from anatomically accurate 3D digital prostate models derived from real clinical MRI/CT scans and ex vivo ultrasound measurements, annotated by medical experts. Simulations are conducted under clinically realistic configurations using advanced finite-difference time-domain and Runge-Kutta acoustic wave solvers, both provided as open-source components. Through comprehensive baseline experiments, we demonstrate that state-of-the-art deep learning methods surpass traditional physics-based approaches in both inference efficiency and reconstruction accuracy. Nevertheless, current deep learning models still fall short of delivering clinically acceptable high-resolution images with sufficient accuracy. By publicly releasing OpenPros, we aim to encourage the development of advanced machine learning algorithms capable of bridging this performance gap and producing clinically usable, high-resolution, and highly accurate prostate ultrasound images. The dataset is publicly accessible at https://open-pros.github.io/.

Towards Artificial Intelligence Research Assistant for Expert-Involved Learning

Large Language Models (LLMs) and Large Multi-Modal Models (LMMs) have emerged as transformative tools in scientific research, yet their reliability and specific contributions to biomedical applications remain insufficiently characterized. In this study, we present \textbf{AR}tificial \textbf{I}ntelligence research assistant for \textbf{E}xpert-involved \textbf{L}earning (ARIEL), a multimodal dataset designed to benchmark and enhance two critical capabilities of LLMs and LMMs in biomedical research: summarizing extensive scientific texts and interpreting complex biomedical figures. To facilitate rigorous assessment, we create two open-source sets comprising biomedical articles and figures with designed questions. We systematically benchmark both open- and closed-source foundation models, incorporating expert-driven human evaluations conducted by doctoral-level experts. Furthermore, we improve model performance through targeted prompt engineering and fine-tuning strategies for summarizing research papers, and apply test-time computational scaling to enhance the reasoning capabilities of LMMs, achieving superior accuracy compared to human-expert corrections. We also explore the potential of using LMM Agents to generate scientific hypotheses from diverse multimodal inputs. Overall, our results delineate clear strengths and highlight significant limitations of current foundation models, providing actionable insights and guiding future advancements in deploying large-scale language and multi-modal models within biomedical research.

Learned Correction Methods for Ultrasound Computed Tomography Imaging Using Simplified Physics Models

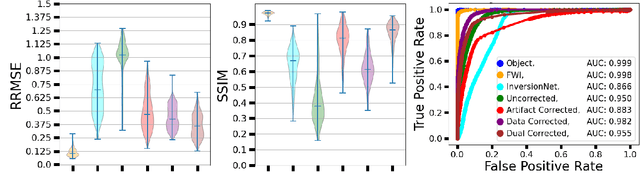
Ultrasound computed tomography (USCT) is an emerging modality for breast imaging. Image reconstruction methods that incorporate accurate wave physics produce high resolution quantitative images of acoustic properties but are computationally expensive. The use of a simplified linear model in reconstruction reduces computational expense at the cost of reduced accuracy. This work aims to systematically compare different learning approaches for USCT reconstruction utilizing simplified linear models. This work considered various learning approaches to compensate for errors stemming from a linearized wave propagation model: correction in the data and image domains. The resulting image reconstruction methods are systematically assessed, alongside data-driven and model-based methods, in four virtual imaging studies utilizing anatomically realistic numerical phantoms. Image quality was assessed utilizing relative root mean square error (RRMSE), structural similarity index measure (SSIM), and a task-based assessment for tumor detection. Correction in the measurement domain resulted in images with minor visual artifacts and highly accurate task performance. Correction in the image domain demonstrated a heavy bias on training data, resulting in hallucinations, but greater robustness to measurement noise. Combining both forms of correction performed best in terms of RRMSE and SSIM, at the cost of task performance. This work systematically assessed learned reconstruction methods incorporating an approximated physical model for USCT imaging. Results demonstrated the importance of incorporating physics, compared to data-driven methods. Learning a correction in the data domain led to better task performance and robust out-of-distribution generalization compared to correction in the image domain.

3D Interaction Geometric Pre-training for Molecular Relational Learning

Molecular Relational Learning (MRL) is a rapidly growing field that focuses on understanding the interaction dynamics between molecules, which is crucial for applications ranging from catalyst engineering to drug discovery. Despite recent progress, earlier MRL approaches are limited to using only the 2D topological structure of molecules, as obtaining the 3D interaction geometry remains prohibitively expensive. This paper introduces a novel 3D geometric pre-training strategy for MRL (3DMRL) that incorporates a 3D virtual interaction environment, overcoming the limitations of costly traditional quantum mechanical calculation methods. With the constructed 3D virtual interaction environment, 3DMRL trains 2D MRL model to learn the overall 3D geometric information of molecular interaction through contrastive learning. Moreover, fine-grained interaction between molecules is learned through force prediction loss, which is crucial in understanding the wide range of molecular interaction processes. Extensive experiments on various tasks using real-world datasets, including out-of-distribution and extrapolation scenarios, demonstrate the effectiveness of 3DMRL, showing up to a 24.93\% improvement in performance across 40 tasks.

Fine-Tuning Discrete Diffusion Models via Reward Optimization with Applications to DNA and Protein Design

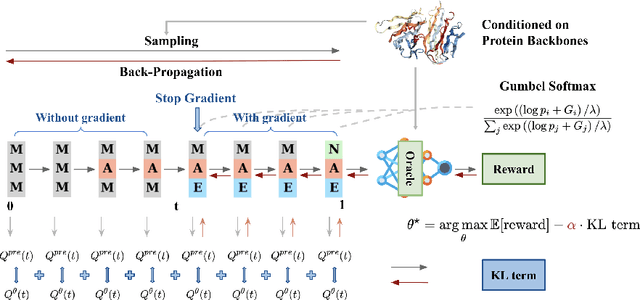
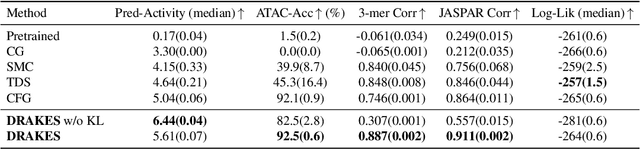
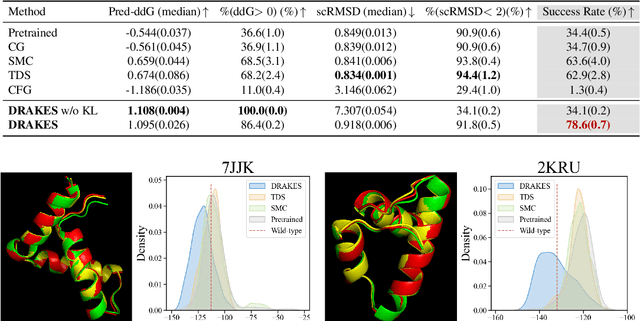
Recent studies have demonstrated the strong empirical performance of diffusion models on discrete sequences across domains from natural language to biological sequence generation. For example, in the protein inverse folding task, conditional diffusion models have achieved impressive results in generating natural-like sequences that fold back into the original structure. However, practical design tasks often require not only modeling a conditional distribution but also optimizing specific task objectives. For instance, we may prefer protein sequences with high stability. To address this, we consider the scenario where we have pre-trained discrete diffusion models that can generate natural-like sequences, as well as reward models that map sequences to task objectives. We then formulate the reward maximization problem within discrete diffusion models, analogous to reinforcement learning (RL), while minimizing the KL divergence against pretrained diffusion models to preserve naturalness. To solve this RL problem, we propose a novel algorithm, DRAKES, that enables direct backpropagation of rewards through entire trajectories generated by diffusion models, by making the originally non-differentiable trajectories differentiable using the Gumbel-Softmax trick. Our theoretical analysis indicates that our approach can generate sequences that are both natural-like and yield high rewards. While similar tasks have been recently explored in diffusion models for continuous domains, our work addresses unique algorithmic and theoretical challenges specific to discrete diffusion models, which arise from their foundation in continuous-time Markov chains rather than Brownian motion. Finally, we demonstrate the effectiveness of DRAKES in generating DNA and protein sequences that optimize enhancer activity and protein stability, respectively, important tasks for gene therapies and protein-based therapeutics.

Bridging Large Language Models and Graph Structure Learning Models for Robust Representation Learning

Graph representation learning, involving both node features and graph structures, is crucial for real-world applications but often encounters pervasive noise. State-of-the-art methods typically address noise by focusing separately on node features with large language models (LLMs) and on graph structures with graph structure learning models (GSLMs). In this paper, we introduce LangGSL, a robust framework that integrates the complementary strengths of pre-trained language models and GSLMs to jointly enhance both node feature and graph structure learning. In LangGSL, we first leverage LLMs to filter noise in the raw data and extract valuable cleaned information as features, enhancing the synergy of downstream models. During the mutual learning phase in LangGSL, the core idea is to leverage the relatively small language model (LM) to process local attributes and generate reliable pseudo-labels and informative node embeddings, which are then integrated into the GSLM's prediction phase. This approach enriches the global context and enhances overall performance. Meanwhile, GSLM refines the evolving graph structure constructed from the LM's output, offering updated labels back to the LM as additional guidance, thus facilitating a more effective mutual learning process. The LM and GSLM work synergistically, complementing each other's strengths and offsetting weaknesses within a variational information-maximizing framework, resulting in enhanced node features and a more robust graph structure. Extensive experiments on diverse graph datasets of varying scales and across different task scenarios demonstrate the scalability and effectiveness of the proposed approach.

RIDA: A Robust Attack Framework on Incomplete Graphs

Graph Neural Networks (GNNs) are vital in data science but are increasingly susceptible to adversarial attacks. To help researchers develop more robust GNN models, it's essential to focus on designing strong attack models as foundational benchmarks and guiding references. Among adversarial attacks, gray-box poisoning attacks are noteworthy due to their effectiveness and fewer constraints. These attacks exploit GNNs' need for retraining on updated data, thereby impacting their performance by perturbing these datasets. However, current research overlooks the real-world scenario of incomplete graphs.To address this gap, we introduce the Robust Incomplete Deep Attack Framework (RIDA). It is the first algorithm for robust gray-box poisoning attacks on incomplete graphs. The approach innovatively aggregates distant vertex information and ensures powerful data utilization.Extensive tests against 9 SOTA baselines on 3 real-world datasets demonstrate RIDA's superiority in handling incompleteness and high attack performance on the incomplete graph.

APS-USCT: Ultrasound Computed Tomography on Sparse Data via AI-Physic Synergy

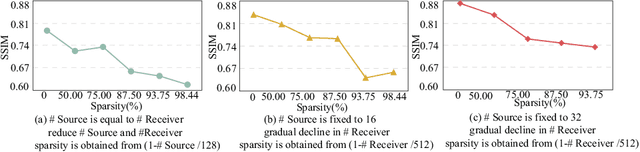
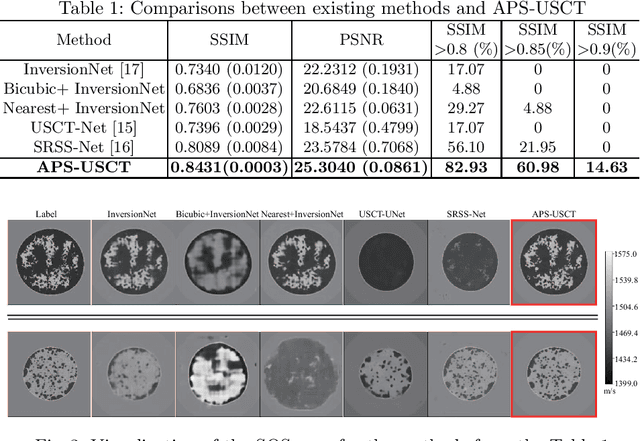
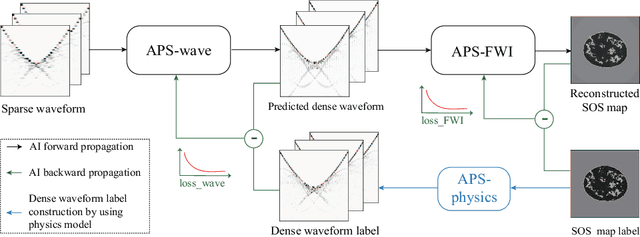
Ultrasound computed tomography (USCT) is a promising technique that achieves superior medical imaging reconstruction resolution by fully leveraging waveform information, outperforming conventional ultrasound methods. Despite its advantages, high-quality USCT reconstruction relies on extensive data acquisition by a large number of transducers, leading to increased costs, computational demands, extended patient scanning times, and manufacturing complexities. To mitigate these issues, we propose a new USCT method called APS-USCT, which facilitates imaging with sparse data, substantially reducing dependence on high-cost dense data acquisition. Our APS-USCT method consists of two primary components: APS-wave and APS-FWI. The APS-wave component, an encoder-decoder system, preprocesses the waveform data, converting sparse data into dense waveforms to augment sample density prior to reconstruction. The APS-FWI component, utilizing the InversionNet, directly reconstructs the speed of sound (SOS) from the ultrasound waveform data. We further improve the model's performance by incorporating Squeeze-and-Excitation (SE) Blocks and source encoding techniques. Testing our method on a breast cancer dataset yielded promising results. It demonstrated outstanding performance with an average Structural Similarity Index (SSIM) of 0.8431. Notably, over 82% of samples achieved an SSIM above 0.8, with nearly 61% exceeding 0.85, highlighting the significant potential of our approach in improving USCT image reconstruction by efficiently utilizing sparse data.