Yinan Feng
On a Hidden Property in Computational Imaging
Oct 11, 2024Abstract:Computational imaging plays a vital role in various scientific and medical applications, such as Full Waveform Inversion (FWI), Computed Tomography (CT), and Electromagnetic (EM) inversion. These methods address inverse problems by reconstructing physical properties (e.g., the acoustic velocity map in FWI) from measurement data (e.g., seismic waveform data in FWI), where both modalities are governed by complex mathematical equations. In this paper, we empirically demonstrate that despite their differing governing equations, three inverse problems (FWI, CT, and EM inversion) share a hidden property within their latent spaces. Specifically, using FWI as an example, we show that both modalities (the velocity map and seismic waveform data) follow the same set of one-way wave equations in the latent space, yet have distinct initial conditions that are linearly correlated. This suggests that after projection into the latent embedding space, the two modalities correspond to different solutions of the same equation, connected through their initial conditions. Our experiments confirm that this hidden property is consistent across all three imaging problems, providing a novel perspective for understanding these computational imaging tasks.
Does Full Waveform Inversion Benefit from Big Data?
Jul 28, 2023Abstract:This paper investigates the impact of big data on deep learning models for full waveform inversion (FWI). While it is well known that big data can boost the performance of deep learning models in many tasks, its effectiveness has not been validated for FWI. To address this gap, we present an empirical study that investigates how deep learning models in FWI behave when trained on OpenFWI, a collection of large-scale, multi-structural datasets published recently. Particularly, we train and evaluate the FWI models on a combination of 10 2D subsets in OpenFWI that contain 470K data pairs in total. Our experiments demonstrate that larger datasets lead to better performance and generalization of deep learning models for FWI. We further demonstrate that model capacity needs to scale in accordance with data size for optimal improvement.
$\mathbf{\mathbb{E}^{FWI}}$: Multi-parameter Benchmark Datasets for Elastic Full Waveform Inversion of Geophysical Properties
Jun 21, 2023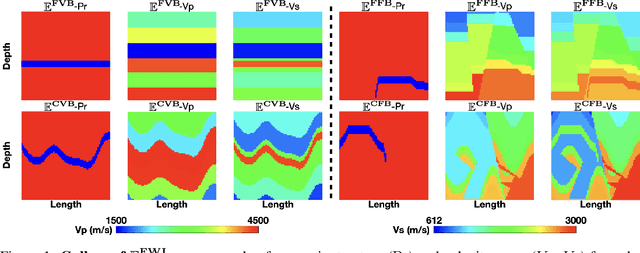

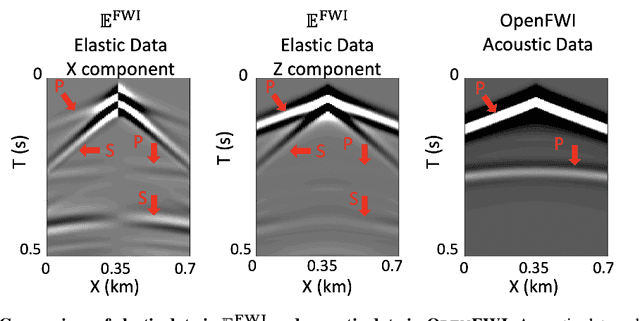

Abstract:Elastic geophysical properties (such as P- and S-wave velocities) are of great importance to various subsurface applications like CO$_2$ sequestration and energy exploration (e.g., hydrogen and geothermal). Elastic full waveform inversion (FWI) is widely applied for characterizing reservoir properties. In this paper, we introduce $\mathbf{\mathbb{E}^{FWI}}$, a comprehensive benchmark dataset that is specifically designed for elastic FWI. $\mathbf{\mathbb{E}^{FWI}}$ encompasses 8 distinct datasets that cover diverse subsurface geologic structures (flat, curve, faults, etc). The benchmark results produced by three different deep learning methods are provided. In contrast to our previously presented dataset (pressure recordings) for acoustic FWI (referred to as OpenFWI), the seismic dataset in $\mathbf{\mathbb{E}^{FWI}}$ has both vertical and horizontal components. Moreover, the velocity maps in $\mathbf{\mathbb{E}^{FWI}}$ incorporate both P- and S-wave velocities. While the multicomponent data and the added S-wave velocity make the data more realistic, more challenges are introduced regarding the convergence and computational cost of the inversion. We conduct comprehensive numerical experiments to explore the relationship between P-wave and S-wave velocities in seismic data. The relation between P- and S-wave velocities provides crucial insights into the subsurface properties such as lithology, porosity, fluid content, etc. We anticipate that $\mathbf{\mathbb{E}^{FWI}}$ will facilitate future research on multiparameter inversions and stimulate endeavors in several critical research topics of carbon-zero and new energy exploration. All datasets, codes and relevant information can be accessed through our website at https://efwi-lanl.github.io/
An Intriguing Property of Geophysics Inversion
Apr 28, 2022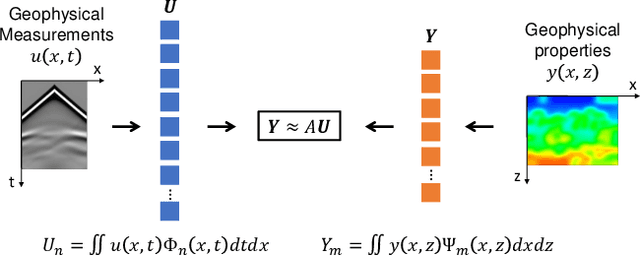
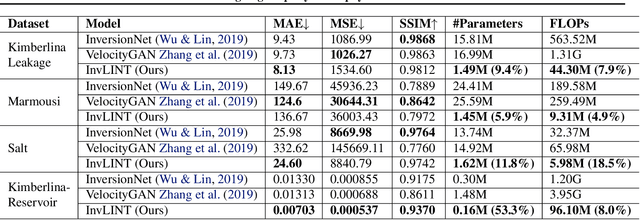
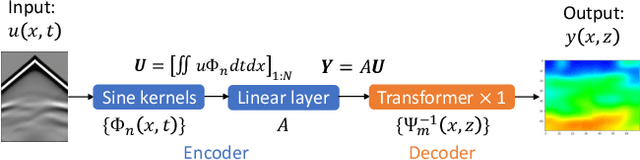
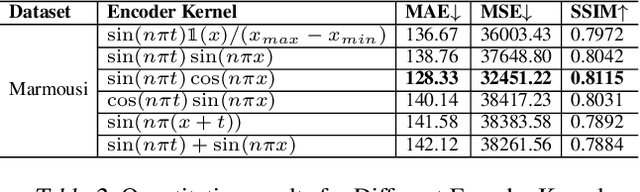
Abstract:Inversion techniques are widely used to reconstruct subsurface physical properties (e.g., velocity, conductivity, and others) from surface-based geophysical measurements (e.g., seismic, electric/magnetic (EM) data). The problems are governed by partial differential equations~(PDEs) like the wave or Maxwell's equations. Solving geophysical inversion problems is challenging due to the ill-posedness and high computational cost. To alleviate those issues, recent studies leverage deep neural networks to learn the inversion mappings from geophysical measurements to the geophysical property directly. In this paper, we show that such a mapping can be well modeled by a \textit{very shallow}~(but not wide) network with only five layers. This is achieved based on our new finding of an intriguing property: \textit{a near-linear relationship between the input and output, after applying integral transform in high dimensional space.} In particular, when dealing with the inversion from seismic data to subsurface velocity governed by a wave equation, the integral results of velocity with Gaussian kernels are linearly correlated to the integral of seismic data with sine kernels. Furthermore, this property can be easily turned into a light-weight encoder-decoder network for inversion. The encoder contains the integration of seismic data and the linear transformation without need for fine-tuning. The decoder only consists of a single transformer block to reverse the integral of velocity. Experiments show that this interesting property holds for two geophysics inversion problems over four different datasets. Compared to much deeper InversionNet~\cite{wu2019inversionnet}, our method achieves comparable accuracy, but consumes significantly fewer parameters.
OpenFWI: Benchmark Seismic Datasets for Machine Learning-Based Full Waveform Inversion
Nov 04, 2021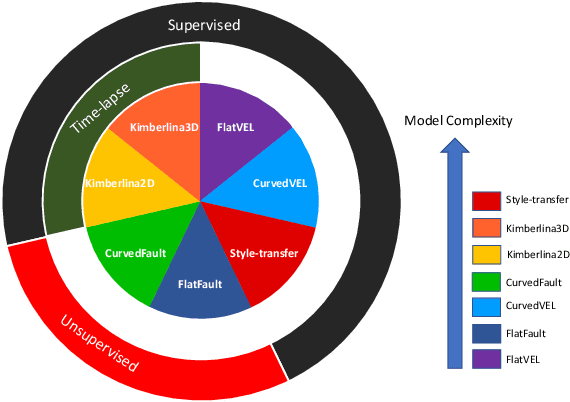
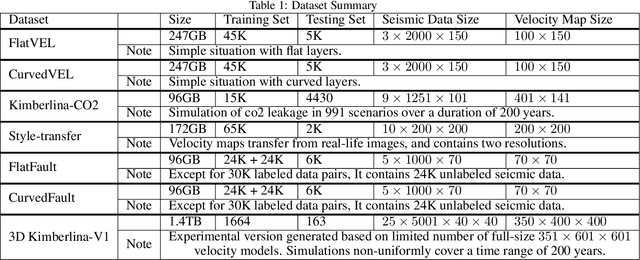
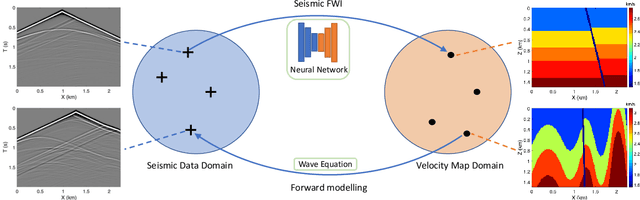
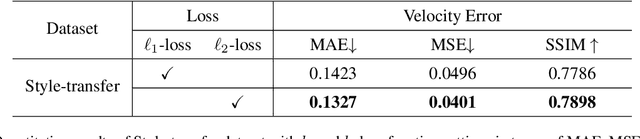
Abstract:We present OpenFWI, a collection of large-scale open-source benchmark datasets for seismic full waveform inversion (FWI). OpenFWI is the first-of-its-kind in the geoscience and machine learning community to facilitate diversified, rigorous, and reproducible research on machine learning-based FWI. OpenFWI includes datasets of multiple scales, encompasses diverse domains, and covers various levels of model complexity. Along with the dataset, we also perform an empirical study on each dataset with a fully-convolutional deep learning model. OpenFWI has been meticulously maintained and will be regularly updated with new data and experimental results. We appreciate the inputs from the community to help us further improve OpenFWI. At the current version, we publish seven datasets in OpenFWI, of which one is specified for 3D FWI and the rest are for 2D scenarios. All datasets and related information can be accessed through our website at https://openfwi.github.io/.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge