OpenPros: A Large-Scale Dataset for Limited View Prostate Ultrasound Computed Tomography

Prostate cancer is one of the most common and lethal cancers among men, making its early detection critically important. Although ultrasound imaging offers greater accessibility and cost-effectiveness compared to MRI, traditional transrectal ultrasound methods suffer from low sensitivity, especially in detecting anteriorly located tumors. Ultrasound computed tomography provides quantitative tissue characterization, but its clinical implementation faces significant challenges, particularly under anatomically constrained limited-angle acquisition conditions specific to prostate imaging. To address these unmet needs, we introduce OpenPros, the first large-scale benchmark dataset explicitly developed for limited-view prostate USCT. Our dataset includes over 280,000 paired samples of realistic 2D speed-of-sound (SOS) phantoms and corresponding ultrasound full-waveform data, generated from anatomically accurate 3D digital prostate models derived from real clinical MRI/CT scans and ex vivo ultrasound measurements, annotated by medical experts. Simulations are conducted under clinically realistic configurations using advanced finite-difference time-domain and Runge-Kutta acoustic wave solvers, both provided as open-source components. Through comprehensive baseline experiments, we demonstrate that state-of-the-art deep learning methods surpass traditional physics-based approaches in both inference efficiency and reconstruction accuracy. Nevertheless, current deep learning models still fall short of delivering clinically acceptable high-resolution images with sufficient accuracy. By publicly releasing OpenPros, we aim to encourage the development of advanced machine learning algorithms capable of bridging this performance gap and producing clinically usable, high-resolution, and highly accurate prostate ultrasound images. The dataset is publicly accessible at https://open-pros.github.io/.

Learned Correction Methods for Ultrasound Computed Tomography Imaging Using Simplified Physics Models

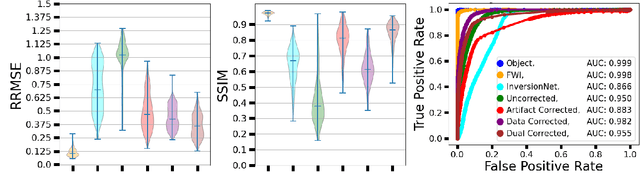
Ultrasound computed tomography (USCT) is an emerging modality for breast imaging. Image reconstruction methods that incorporate accurate wave physics produce high resolution quantitative images of acoustic properties but are computationally expensive. The use of a simplified linear model in reconstruction reduces computational expense at the cost of reduced accuracy. This work aims to systematically compare different learning approaches for USCT reconstruction utilizing simplified linear models. This work considered various learning approaches to compensate for errors stemming from a linearized wave propagation model: correction in the data and image domains. The resulting image reconstruction methods are systematically assessed, alongside data-driven and model-based methods, in four virtual imaging studies utilizing anatomically realistic numerical phantoms. Image quality was assessed utilizing relative root mean square error (RRMSE), structural similarity index measure (SSIM), and a task-based assessment for tumor detection. Correction in the measurement domain resulted in images with minor visual artifacts and highly accurate task performance. Correction in the image domain demonstrated a heavy bias on training data, resulting in hallucinations, but greater robustness to measurement noise. Combining both forms of correction performed best in terms of RRMSE and SSIM, at the cost of task performance. This work systematically assessed learned reconstruction methods incorporating an approximated physical model for USCT imaging. Results demonstrated the importance of incorporating physics, compared to data-driven methods. Learning a correction in the data domain led to better task performance and robust out-of-distribution generalization compared to correction in the image domain.

A Novel Diffusion Model for Pairwise Geoscience Data Generation with Unbalanced Training Dataset

Recently, the advent of generative AI technologies has made transformational impacts on our daily lives, yet its application in scientific applications remains in its early stages. Data scarcity is a major, well-known barrier in data-driven scientific computing, so physics-guided generative AI holds significant promise. In scientific computing, most tasks study the conversion of multiple data modalities to describe physical phenomena, for example, spatial and waveform in seismic imaging, time and frequency in signal processing, and temporal and spectral in climate modeling; as such, multi-modal pairwise data generation is highly required instead of single-modal data generation, which is usually used in natural images (e.g., faces, scenery). Moreover, in real-world applications, the unbalance of available data in terms of modalities commonly exists; for example, the spatial data (i.e., velocity maps) in seismic imaging can be easily simulated, but real-world seismic waveform is largely lacking. While the most recent efforts enable the powerful diffusion model to generate multi-modal data, how to leverage the unbalanced available data is still unclear. In this work, we use seismic imaging in subsurface geophysics as a vehicle to present ``UB-Diff'', a novel diffusion model for multi-modal paired scientific data generation. One major innovation is a one-in-two-out encoder-decoder network structure, which can ensure pairwise data is obtained from a co-latent representation. Then, the co-latent representation will be used by the diffusion process for pairwise data generation. Experimental results on the OpenFWI dataset show that UB-Diff significantly outperforms existing techniques in terms of Fr\'{e}chet Inception Distance (FID) score and pairwise evaluation, indicating the generation of reliable and useful multi-modal pairwise data.

A Unified Framework for Forward and Inverse Problems in Subsurface Imaging using Latent Space Translations

In subsurface imaging, learning the mapping from velocity maps to seismic waveforms (forward problem) and waveforms to velocity (inverse problem) is important for several applications. While traditional techniques for solving forward and inverse problems are computationally prohibitive, there is a growing interest in leveraging recent advances in deep learning to learn the mapping between velocity maps and seismic waveform images directly from data. Despite the variety of architectures explored in previous works, several open questions still remain unanswered such as the effect of latent space sizes, the importance of manifold learning, the complexity of translation models, and the value of jointly solving forward and inverse problems. We propose a unified framework to systematically characterize prior research in this area termed the Generalized Forward-Inverse (GFI) framework, building on the assumption of manifolds and latent space translations. We show that GFI encompasses previous works in deep learning for subsurface imaging, which can be viewed as specific instantiations of GFI. We also propose two new model architectures within the framework of GFI: Latent U-Net and Invertible X-Net, leveraging the power of U-Nets for domain translation and the ability of IU-Nets to simultaneously learn forward and inverse translations, respectively. We show that our proposed models achieve state-of-the-art (SOTA) performance for forward and inverse problems on a wide range of synthetic datasets, and also investigate their zero-shot effectiveness on two real-world-like datasets.

On a Hidden Property in Computational Imaging

Computational imaging plays a vital role in various scientific and medical applications, such as Full Waveform Inversion (FWI), Computed Tomography (CT), and Electromagnetic (EM) inversion. These methods address inverse problems by reconstructing physical properties (e.g., the acoustic velocity map in FWI) from measurement data (e.g., seismic waveform data in FWI), where both modalities are governed by complex mathematical equations. In this paper, we empirically demonstrate that despite their differing governing equations, three inverse problems (FWI, CT, and EM inversion) share a hidden property within their latent spaces. Specifically, using FWI as an example, we show that both modalities (the velocity map and seismic waveform data) follow the same set of one-way wave equations in the latent space, yet have distinct initial conditions that are linearly correlated. This suggests that after projection into the latent embedding space, the two modalities correspond to different solutions of the same equation, connected through their initial conditions. Our experiments confirm that this hidden property is consistent across all three imaging problems, providing a novel perspective for understanding these computational imaging tasks.

Physics and Deep Learning in Computational Wave Imaging

Computational wave imaging (CWI) extracts hidden structure and physical properties of a volume of material by analyzing wave signals that traverse that volume. Applications include seismic exploration of the Earth's subsurface, acoustic imaging and non-destructive testing in material science, and ultrasound computed tomography in medicine. Current approaches for solving CWI problems can be divided into two categories: those rooted in traditional physics, and those based on deep learning. Physics-based methods stand out for their ability to provide high-resolution and quantitatively accurate estimates of acoustic properties within the medium. However, they can be computationally intensive and are susceptible to ill-posedness and nonconvexity typical of CWI problems. Machine learning-based computational methods have recently emerged, offering a different perspective to address these challenges. Diverse scientific communities have independently pursued the integration of deep learning in CWI. This review delves into how contemporary scientific machine-learning (ML) techniques, and deep neural networks in particular, have been harnessed to tackle CWI problems. We present a structured framework that consolidates existing research spanning multiple domains, including computational imaging, wave physics, and data science. This study concludes with important lessons learned from existing ML-based methods and identifies technical hurdles and emerging trends through a systematic analysis of the extensive literature on this topic.

APS-USCT: Ultrasound Computed Tomography on Sparse Data via AI-Physic Synergy

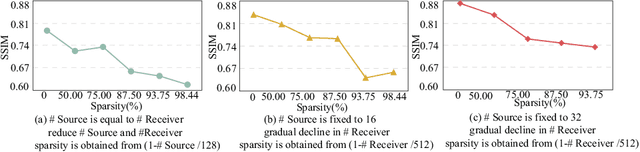
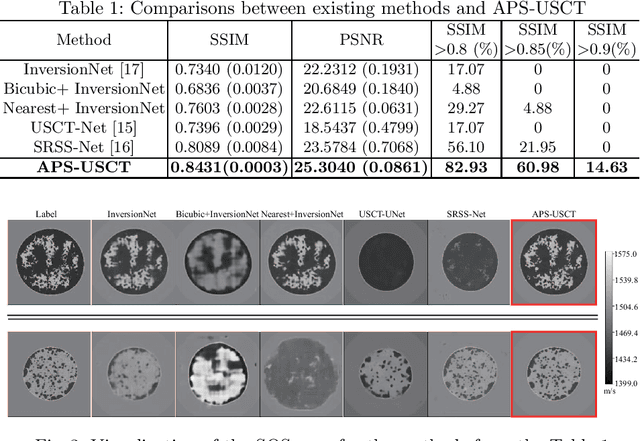
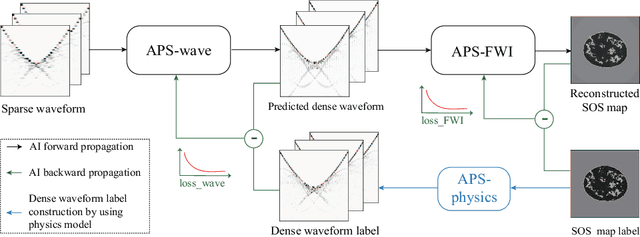
Ultrasound computed tomography (USCT) is a promising technique that achieves superior medical imaging reconstruction resolution by fully leveraging waveform information, outperforming conventional ultrasound methods. Despite its advantages, high-quality USCT reconstruction relies on extensive data acquisition by a large number of transducers, leading to increased costs, computational demands, extended patient scanning times, and manufacturing complexities. To mitigate these issues, we propose a new USCT method called APS-USCT, which facilitates imaging with sparse data, substantially reducing dependence on high-cost dense data acquisition. Our APS-USCT method consists of two primary components: APS-wave and APS-FWI. The APS-wave component, an encoder-decoder system, preprocesses the waveform data, converting sparse data into dense waveforms to augment sample density prior to reconstruction. The APS-FWI component, utilizing the InversionNet, directly reconstructs the speed of sound (SOS) from the ultrasound waveform data. We further improve the model's performance by incorporating Squeeze-and-Excitation (SE) Blocks and source encoding techniques. Testing our method on a breast cancer dataset yielded promising results. It demonstrated outstanding performance with an average Structural Similarity Index (SSIM) of 0.8431. Notably, over 82% of samples achieved an SSIM above 0.8, with nearly 61% exceeding 0.85, highlighting the significant potential of our approach in improving USCT image reconstruction by efficiently utilizing sparse data.

A Physics-guided Generative AI Toolkit for Geophysical Monitoring

Full-waveform inversion (FWI) plays a vital role in geoscience to explore the subsurface. It utilizes the seismic wave to image the subsurface velocity map. As the machine learning (ML) technique evolves, the data-driven approaches using ML for FWI tasks have emerged, offering enhanced accuracy and reduced computational cost compared to traditional physics-based methods. However, a common challenge in geoscience, the unprivileged data, severely limits ML effectiveness. The issue becomes even worse during model pruning, a step essential in geoscience due to environmental complexities. To tackle this, we introduce the EdGeo toolkit, which employs a diffusion-based model guided by physics principles to generate high-fidelity velocity maps. The toolkit uses the acoustic wave equation to generate corresponding seismic waveform data, facilitating the fine-tuning of pruned ML models. Our results demonstrate significant improvements in SSIM scores and reduction in both MAE and MSE across various pruning ratios. Notably, the ML model fine-tuned using data generated by EdGeo yields superior quality of velocity maps, especially in representing unprivileged features, outperforming other existing methods.

On the Hidden Waves of Image

In this paper, we introduce an intriguing phenomenon-the successful reconstruction of images using a set of one-way wave equations with hidden and learnable speeds. Each individual image corresponds to a solution with a unique initial condition, which can be computed from the original image using a visual encoder (e.g., a convolutional neural network). Furthermore, the solution for each image exhibits two noteworthy mathematical properties: (a) it can be decomposed into a collection of special solutions of the same one-way wave equations that are first-order autoregressive, with shared coefficient matrices for autoregression, and (b) the product of these coefficient matrices forms a diagonal matrix with the speeds of the wave equations as its diagonal elements. We term this phenomenon hidden waves, as it reveals that, although the speeds of the set of wave equations and autoregressive coefficient matrices are latent, they are both learnable and shared across images. This represents a mathematical invariance across images, providing a new mathematical perspective to understand images.

Edge-InversionNet: Enabling Efficient Inference of InversionNet on Edge Devices

Seismic full waveform inversion (FWI) is a widely used technique in geophysics for inferring subsurface structures from seismic data. And InversionNet is one of the most successful data-driven machine learning models that is applied to seismic FWI. However, the high computing costs to run InversionNet have made it challenging to be efficiently deployed on edge devices that are usually resource-constrained. Therefore, we propose to employ the structured pruning algorithm to get a lightweight version of InversionNet, which can make an efficient inference on edge devices. And we also made a prototype with Raspberry Pi to run the lightweight InversionNet. Experimental results show that the pruned InversionNet can achieve up to 98.2 % reduction in computing resources with moderate model performance degradation.