Improving Full Waveform Inversion in Large Model Era

Full Waveform Inversion (FWI) is a highly nonlinear and ill-posed problem that aims to recover subsurface velocity maps from surface-recorded seismic waveforms data. Existing data-driven FWI typically uses small models, as available datasets have limited volume, geological diversity, and spatial extent, leading to substantial concerns about overfitting. Although they perform well on synthetic datasets, current methods fail to generalize to more realistic geological structures. In this work, we show that a model trained entirely on simulated and relatively simple data can generalize remarkably well to challenging and unseen geological benchmarks. We provide a working recipe that tames a billion-parameter model for FWI through coordinated scaling across three axes: model capacity, data diversity, and training strategy. Our model achieves state-of-the-art performance on OpenFWI and significantly narrows the generalization gap in data-driven FWI. Across six challenging geophysical benchmarks, including Marmousi, 2D SEG/EAGE Salt and Overthrust, 2004 BP, Sigsbee, and SEAM Phase I, it infers complex structures absent from the training set and delivers significant performance improvements (SSIM from 0.5844 to 0.7669). Overall, our results demonstrate that with an appropriate scaling strategy, large models trained on simple synthetic data can achieve substantial generalization to more complex and realistic geological structures.

OpenPros: A Large-Scale Dataset for Limited View Prostate Ultrasound Computed Tomography

Prostate cancer is one of the most common and lethal cancers among men, making its early detection critically important. Although ultrasound imaging offers greater accessibility and cost-effectiveness compared to MRI, traditional transrectal ultrasound methods suffer from low sensitivity, especially in detecting anteriorly located tumors. Ultrasound computed tomography provides quantitative tissue characterization, but its clinical implementation faces significant challenges, particularly under anatomically constrained limited-angle acquisition conditions specific to prostate imaging. To address these unmet needs, we introduce OpenPros, the first large-scale benchmark dataset explicitly developed for limited-view prostate USCT. Our dataset includes over 280,000 paired samples of realistic 2D speed-of-sound (SOS) phantoms and corresponding ultrasound full-waveform data, generated from anatomically accurate 3D digital prostate models derived from real clinical MRI/CT scans and ex vivo ultrasound measurements, annotated by medical experts. Simulations are conducted under clinically realistic configurations using advanced finite-difference time-domain and Runge-Kutta acoustic wave solvers, both provided as open-source components. Through comprehensive baseline experiments, we demonstrate that state-of-the-art deep learning methods surpass traditional physics-based approaches in both inference efficiency and reconstruction accuracy. Nevertheless, current deep learning models still fall short of delivering clinically acceptable high-resolution images with sufficient accuracy. By publicly releasing OpenPros, we aim to encourage the development of advanced machine learning algorithms capable of bridging this performance gap and producing clinically usable, high-resolution, and highly accurate prostate ultrasound images. The dataset is publicly accessible at https://open-pros.github.io/.

On a Hidden Property in Computational Imaging

Computational imaging plays a vital role in various scientific and medical applications, such as Full Waveform Inversion (FWI), Computed Tomography (CT), and Electromagnetic (EM) inversion. These methods address inverse problems by reconstructing physical properties (e.g., the acoustic velocity map in FWI) from measurement data (e.g., seismic waveform data in FWI), where both modalities are governed by complex mathematical equations. In this paper, we empirically demonstrate that despite their differing governing equations, three inverse problems (FWI, CT, and EM inversion) share a hidden property within their latent spaces. Specifically, using FWI as an example, we show that both modalities (the velocity map and seismic waveform data) follow the same set of one-way wave equations in the latent space, yet have distinct initial conditions that are linearly correlated. This suggests that after projection into the latent embedding space, the two modalities correspond to different solutions of the same equation, connected through their initial conditions. Our experiments confirm that this hidden property is consistent across all three imaging problems, providing a novel perspective for understanding these computational imaging tasks.

Physics and Deep Learning in Computational Wave Imaging

Computational wave imaging (CWI) extracts hidden structure and physical properties of a volume of material by analyzing wave signals that traverse that volume. Applications include seismic exploration of the Earth's subsurface, acoustic imaging and non-destructive testing in material science, and ultrasound computed tomography in medicine. Current approaches for solving CWI problems can be divided into two categories: those rooted in traditional physics, and those based on deep learning. Physics-based methods stand out for their ability to provide high-resolution and quantitatively accurate estimates of acoustic properties within the medium. However, they can be computationally intensive and are susceptible to ill-posedness and nonconvexity typical of CWI problems. Machine learning-based computational methods have recently emerged, offering a different perspective to address these challenges. Diverse scientific communities have independently pursued the integration of deep learning in CWI. This review delves into how contemporary scientific machine-learning (ML) techniques, and deep neural networks in particular, have been harnessed to tackle CWI problems. We present a structured framework that consolidates existing research spanning multiple domains, including computational imaging, wave physics, and data science. This study concludes with important lessons learned from existing ML-based methods and identifies technical hurdles and emerging trends through a systematic analysis of the extensive literature on this topic.

MELODI: Exploring Memory Compression for Long Contexts

We present MELODI, a novel memory architecture designed to efficiently process long documents using short context windows. The key principle behind MELODI is to represent short-term and long-term memory as a hierarchical compression scheme across both network layers and context windows. Specifically, the short-term memory is achieved through recurrent compression of context windows across multiple layers, ensuring smooth transitions between windows. In contrast, the long-term memory performs further compression within a single middle layer and aggregates information across context windows, effectively consolidating crucial information from the entire history. Compared to a strong baseline - the Memorizing Transformer employing dense attention over a large long-term memory (64K key-value pairs) - our method demonstrates superior performance on various long-context datasets while remarkably reducing the memory footprint by a factor of 8.

Efficient Modulation for Vision Networks

In this work, we present efficient modulation, a novel design for efficient vision networks. We revisit the modulation mechanism, which operates input through convolutional context modeling and feature projection layers, and fuses features via element-wise multiplication and an MLP block. We demonstrate that the modulation mechanism is particularly well suited for efficient networks and further tailor the modulation design by proposing the efficient modulation (EfficientMod) block, which is considered the essential building block for our networks. Benefiting from the prominent representational ability of modulation mechanism and the proposed efficient design, our network can accomplish better trade-offs between accuracy and efficiency and set new state-of-the-art performance in the zoo of efficient networks. When integrating EfficientMod with the vanilla self-attention block, we obtain the hybrid architecture which further improves the performance without loss of efficiency. We carry out comprehensive experiments to verify EfficientMod's performance. With fewer parameters, our EfficientMod-s performs 0.6 top-1 accuracy better than EfficientFormerV2-s2 and is 25% faster on GPU, and 2.9 better than MobileViTv2-1.0 at the same GPU latency. Additionally, our method presents a notable improvement in downstream tasks, outperforming EfficientFormerV2-s by 3.6 mIoU on the ADE20K benchmark. Code and checkpoints are available at https://github.com/ma-xu/EfficientMod.

On the Hidden Waves of Image

In this paper, we introduce an intriguing phenomenon-the successful reconstruction of images using a set of one-way wave equations with hidden and learnable speeds. Each individual image corresponds to a solution with a unique initial condition, which can be computed from the original image using a visual encoder (e.g., a convolutional neural network). Furthermore, the solution for each image exhibits two noteworthy mathematical properties: (a) it can be decomposed into a collection of special solutions of the same one-way wave equations that are first-order autoregressive, with shared coefficient matrices for autoregression, and (b) the product of these coefficient matrices forms a diagonal matrix with the speeds of the wave equations as its diagonal elements. We term this phenomenon hidden waves, as it reveals that, although the speeds of the set of wave equations and autoregressive coefficient matrices are latent, they are both learnable and shared across images. This represents a mathematical invariance across images, providing a new mathematical perspective to understand images.

Learning from Rich Semantics and Coarse Locations for Long-tailed Object Detection

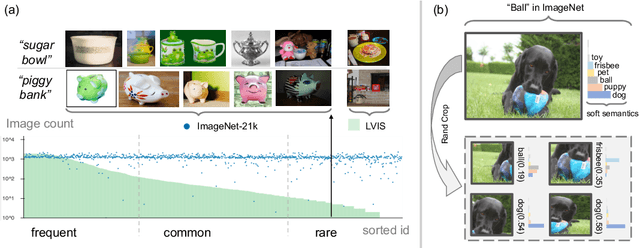
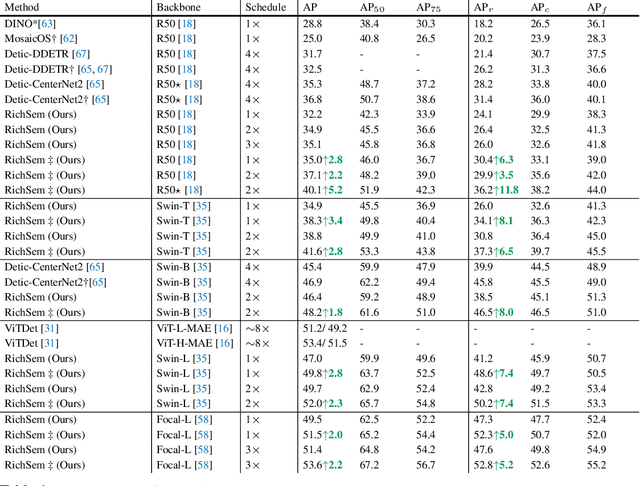
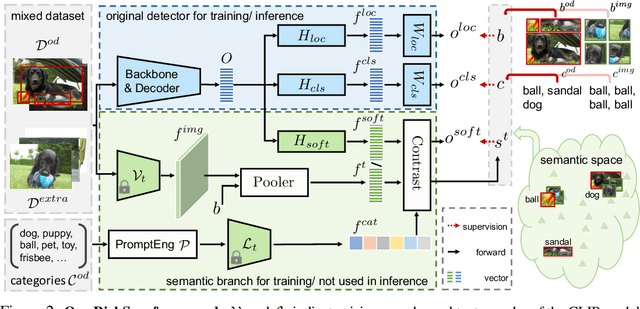
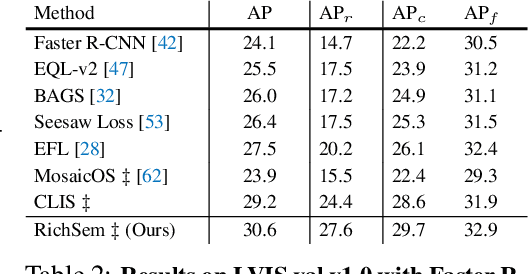
Long-tailed object detection (LTOD) aims to handle the extreme data imbalance in real-world datasets, where many tail classes have scarce instances. One popular strategy is to explore extra data with image-level labels, yet it produces limited results due to (1) semantic ambiguity -- an image-level label only captures a salient part of the image, ignoring the remaining rich semantics within the image; and (2) location sensitivity -- the label highly depends on the locations and crops of the original image, which may change after data transformations like random cropping. To remedy this, we propose RichSem, a simple but effective method, which is robust to learn rich semantics from coarse locations without the need of accurate bounding boxes. RichSem leverages rich semantics from images, which are then served as additional soft supervision for training detectors. Specifically, we add a semantic branch to our detector to learn these soft semantics and enhance feature representations for long-tailed object detection. The semantic branch is only used for training and is removed during inference. RichSem achieves consistent improvements on both overall and rare-category of LVIS under different backbones and detectors. Our method achieves state-of-the-art performance without requiring complex training and testing procedures. Moreover, we show the effectiveness of our method on other long-tailed datasets with additional experiments. Code is available at \url{https://github.com/MengLcool/RichSem}.

Completing Visual Objects via Bridging Generation and Segmentation

This paper presents a novel approach to object completion, with the primary goal of reconstructing a complete object from its partially visible components. Our method, named MaskComp, delineates the completion process through iterative stages of generation and segmentation. In each iteration, the object mask is provided as an additional condition to boost image generation, and, in return, the generated images can lead to a more accurate mask by fusing the segmentation of images. We demonstrate that the combination of one generation and one segmentation stage effectively functions as a mask denoiser. Through alternation between the generation and segmentation stages, the partial object mask is progressively refined, providing precise shape guidance and yielding superior object completion results. Our experiments demonstrate the superiority of MaskComp over existing approaches, e.g., ControlNet and Stable Diffusion, establishing it as an effective solution for object completion.

Improving Adversarial Robustness of Masked Autoencoders via Test-time Frequency-domain Prompting

In this paper, we investigate the adversarial robustness of vision transformers that are equipped with BERT pretraining (e.g., BEiT, MAE). A surprising observation is that MAE has significantly worse adversarial robustness than other BERT pretraining methods. This observation drives us to rethink the basic differences between these BERT pretraining methods and how these differences affect the robustness against adversarial perturbations. Our empirical analysis reveals that the adversarial robustness of BERT pretraining is highly related to the reconstruction target, i.e., predicting the raw pixels of masked image patches will degrade more adversarial robustness of the model than predicting the semantic context, since it guides the model to concentrate more on medium-/high-frequency components of images. Based on our analysis, we provide a simple yet effective way to boost the adversarial robustness of MAE. The basic idea is using the dataset-extracted domain knowledge to occupy the medium-/high-frequency of images, thus narrowing the optimization space of adversarial perturbations. Specifically, we group the distribution of pretraining data and optimize a set of cluster-specific visual prompts on frequency domain. These prompts are incorporated with input images through prototype-based prompt selection during test period. Extensive evaluation shows that our method clearly boost MAE's adversarial robustness while maintaining its clean performance on ImageNet-1k classification. Our code is available at: https://github.com/shikiw/RobustMAE.