Physics and Deep Learning in Computational Wave Imaging

Computational wave imaging (CWI) extracts hidden structure and physical properties of a volume of material by analyzing wave signals that traverse that volume. Applications include seismic exploration of the Earth's subsurface, acoustic imaging and non-destructive testing in material science, and ultrasound computed tomography in medicine. Current approaches for solving CWI problems can be divided into two categories: those rooted in traditional physics, and those based on deep learning. Physics-based methods stand out for their ability to provide high-resolution and quantitatively accurate estimates of acoustic properties within the medium. However, they can be computationally intensive and are susceptible to ill-posedness and nonconvexity typical of CWI problems. Machine learning-based computational methods have recently emerged, offering a different perspective to address these challenges. Diverse scientific communities have independently pursued the integration of deep learning in CWI. This review delves into how contemporary scientific machine-learning (ML) techniques, and deep neural networks in particular, have been harnessed to tackle CWI problems. We present a structured framework that consolidates existing research spanning multiple domains, including computational imaging, wave physics, and data science. This study concludes with important lessons learned from existing ML-based methods and identifies technical hurdles and emerging trends through a systematic analysis of the extensive literature on this topic.

Overview of Physics-Informed Machine Learning Inversion of Geophysical Data

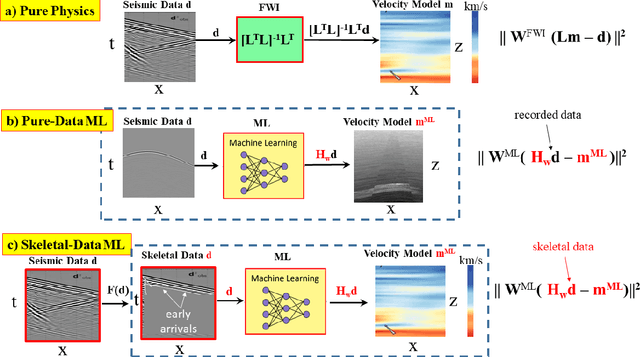
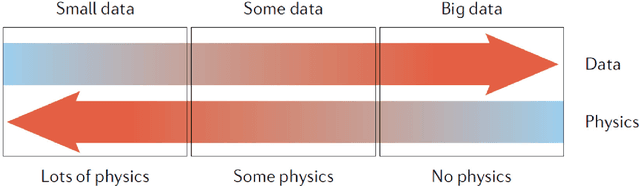
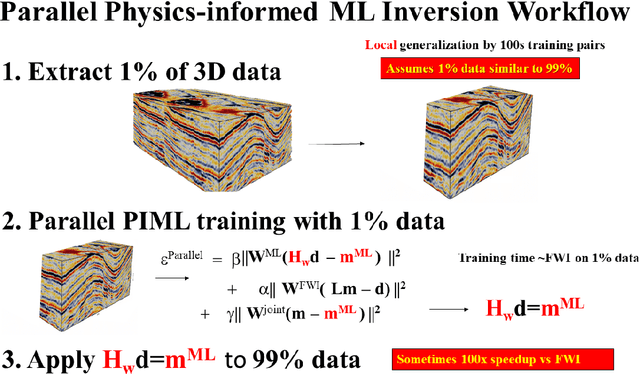
We review four types of algorithms for physics-informed machine learning (PIML) inversion of geophysical data. The unifying equation is given by the joint objective function $\epsilon$: \begin{eqnarray} \epsilon^{||-PIML}&=&\lambda_1 \overbrace{||{\bf W}^{ML}({\bf H}_{{\bf w}} {\bf d}^{obs}-{\bf m})||^2}^{NN} + \lambda_2 \overbrace{{||{\bf W}^{FWI}({\bf L} {\bf m}-{\bf d}^{obs})||^2}}^{FWI} ~+ \nonumber\\ \nonumber\\ && + ~~Regularizer, \label{PIML.eq120} \end{eqnarray}where the optimal model ${\bf m}^*$ and weights $\bf w^*$ minimize $\epsilon$. Here, The matrix weights are given by the boldface symbol $\bf W$, and full waveform inversion (FWI) is typically computed using a finite-difference solution of the wave equation, where $\bf L$ represents the forward modeling operation of the wave equation as a function of the model $\bf m$. Also, a fully-connected neural network (NN) is used to compute the model ${\bf H_w}{\bf d}^{obs} \approx \bf m$ from the observed input data ${\bf d}^{obs}$. The selection of weights $\lambda_i$ and the NN operations determine one of four different PIML algorithms. PIML offers potential advantages over standard FWI through its enhanced ability to avoid local minima and the option to locally train the inversion operator, minimizing the requirement for extensive training data for global applicability. However, the effectiveness of PIML relies on the similarity between the test and trained data. Nevertheless, a possible strategy to overcome this limitation involves initial pretraining of a PIML architecture with data from a broader region, followed by fine-tuning for specific data-a method reminiscent of the way large language models are pretrained and adapted for various tasks.

Does Full Waveform Inversion Benefit from Big Data?

This paper investigates the impact of big data on deep learning models for full waveform inversion (FWI). While it is well known that big data can boost the performance of deep learning models in many tasks, its effectiveness has not been validated for FWI. To address this gap, we present an empirical study that investigates how deep learning models in FWI behave when trained on OpenFWI, a collection of large-scale, multi-structural datasets published recently. Particularly, we train and evaluate the FWI models on a combination of 10 2D subsets in OpenFWI that contain 470K data pairs in total. Our experiments demonstrate that larger datasets lead to better performance and generalization of deep learning models for FWI. We further demonstrate that model capacity needs to scale in accordance with data size for optimal improvement.

$\mathbf{\mathbb{E}^{FWI}}$: Multi-parameter Benchmark Datasets for Elastic Full Waveform Inversion of Geophysical Properties

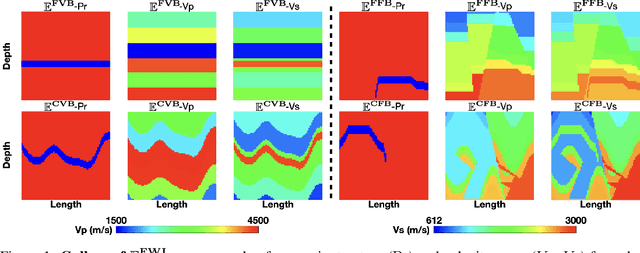
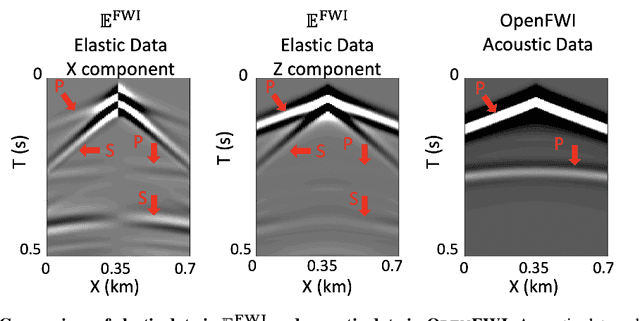
Elastic geophysical properties (such as P- and S-wave velocities) are of great importance to various subsurface applications like CO$_2$ sequestration and energy exploration (e.g., hydrogen and geothermal). Elastic full waveform inversion (FWI) is widely applied for characterizing reservoir properties. In this paper, we introduce $\mathbf{\mathbb{E}^{FWI}}$, a comprehensive benchmark dataset that is specifically designed for elastic FWI. $\mathbf{\mathbb{E}^{FWI}}$ encompasses 8 distinct datasets that cover diverse subsurface geologic structures (flat, curve, faults, etc). The benchmark results produced by three different deep learning methods are provided. In contrast to our previously presented dataset (pressure recordings) for acoustic FWI (referred to as OpenFWI), the seismic dataset in $\mathbf{\mathbb{E}^{FWI}}$ has both vertical and horizontal components. Moreover, the velocity maps in $\mathbf{\mathbb{E}^{FWI}}$ incorporate both P- and S-wave velocities. While the multicomponent data and the added S-wave velocity make the data more realistic, more challenges are introduced regarding the convergence and computational cost of the inversion. We conduct comprehensive numerical experiments to explore the relationship between P-wave and S-wave velocities in seismic data. The relation between P- and S-wave velocities provides crucial insights into the subsurface properties such as lithology, porosity, fluid content, etc. We anticipate that $\mathbf{\mathbb{E}^{FWI}}$ will facilitate future research on multiparameter inversions and stimulate endeavors in several critical research topics of carbon-zero and new energy exploration. All datasets, codes and relevant information can be accessed through our website at https://efwi-lanl.github.io/

HOSSnet: an Efficient Physics-Guided Neural Network for Simulating Crack Propagation

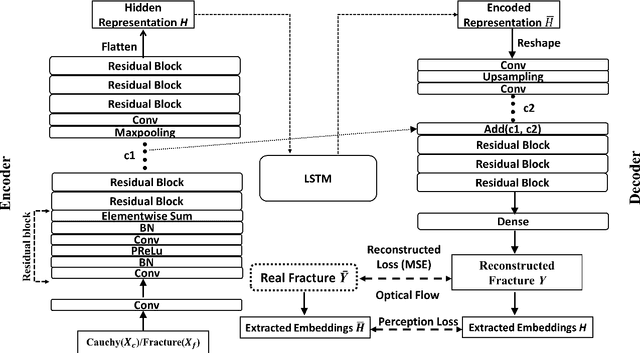
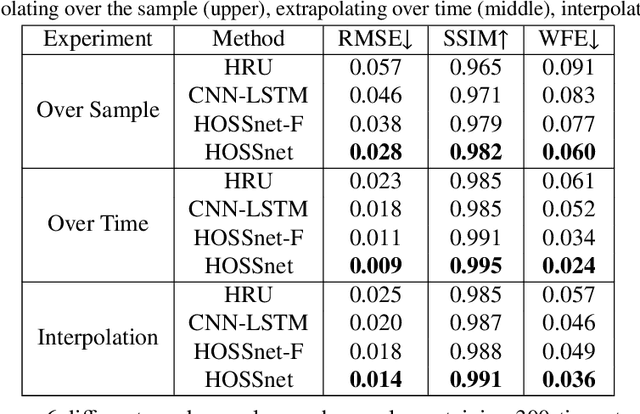
Hybrid Optimization Software Suite (HOSS), which is a combined finite-discrete element method (FDEM), is one of the advanced approaches to simulating high-fidelity fracture and fragmentation processes but the application of pure HOSS simulation is computationally expensive. At the same time, machine learning methods, shown tremendous success in several scientific problems, are increasingly being considered promising alternatives to physics-based models in the scientific domains. Thus, our goal in this work is to build a new data-driven methodology to reconstruct the crack fracture accurately in the spatial and temporal fields. We leverage physical constraints to regularize the fracture propagation in the long-term reconstruction. In addition, we introduce perceptual loss and several extra pure machine learning optimization approaches to improve the reconstruction performance of fracture data further. We demonstrate the effectiveness of our proposed method through both extrapolation and interpolation experiments. The results confirm that our proposed method can reconstruct high-fidelity fracture data over space and time in terms of pixel-wise reconstruction error and structural similarity. Visual comparisons also show promising results in long-term

Fourier-DeepONet: Fourier-enhanced deep operator networks for full waveform inversion with improved accuracy, generalizability, and robustness

Full waveform inversion (FWI) infers the subsurface structure information from seismic waveform data by solving a non-convex optimization problem. Data-driven FWI has been increasingly studied with various neural network architectures to improve accuracy and computational efficiency. Nevertheless, the applicability of pre-trained neural networks is severely restricted by potential discrepancies between the source function used in the field survey and the one utilized during training. Here, we develop a Fourier-enhanced deep operator network (Fourier-DeepONet) for FWI with the generalization of seismic sources, including the frequencies and locations of sources. Specifically, we employ the Fourier neural operator as the decoder of DeepONet, and we utilize source parameters as one input of Fourier-DeepONet, facilitating the resolution of FWI with variable sources. To test Fourier-DeepONet, we develop two new and realistic FWI benchmark datasets (FWI-F and FWI-L) with varying source frequencies and locations. Our experiments demonstrate that compared with existing data-driven FWI methods, Fourier-DeepONet obtains more accurate predictions of subsurface structures in a wide range of source parameters. Moreover, the proposed Fourier-DeepONet exhibits superior robustness when dealing with noisy inputs or inputs with missing traces, paving the way for more reliable and accurate subsurface imaging across diverse real conditions.

An Intriguing Property of Geophysics Inversion

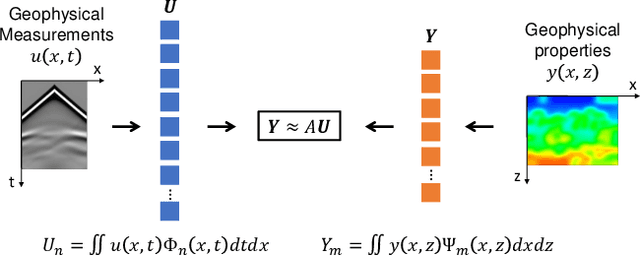
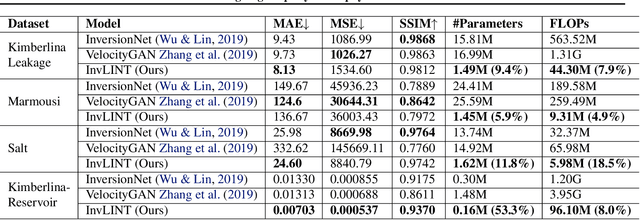
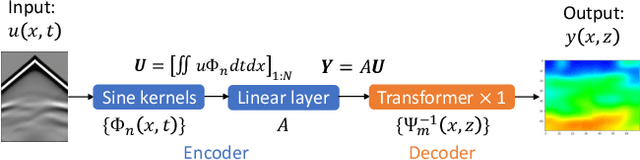
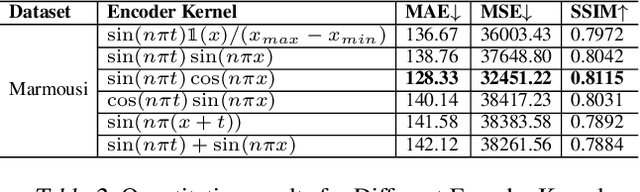
Inversion techniques are widely used to reconstruct subsurface physical properties (e.g., velocity, conductivity, and others) from surface-based geophysical measurements (e.g., seismic, electric/magnetic (EM) data). The problems are governed by partial differential equations~(PDEs) like the wave or Maxwell's equations. Solving geophysical inversion problems is challenging due to the ill-posedness and high computational cost. To alleviate those issues, recent studies leverage deep neural networks to learn the inversion mappings from geophysical measurements to the geophysical property directly. In this paper, we show that such a mapping can be well modeled by a \textit{very shallow}~(but not wide) network with only five layers. This is achieved based on our new finding of an intriguing property: \textit{a near-linear relationship between the input and output, after applying integral transform in high dimensional space.} In particular, when dealing with the inversion from seismic data to subsurface velocity governed by a wave equation, the integral results of velocity with Gaussian kernels are linearly correlated to the integral of seismic data with sine kernels. Furthermore, this property can be easily turned into a light-weight encoder-decoder network for inversion. The encoder contains the integration of seismic data and the linear transformation without need for fine-tuning. The decoder only consists of a single transformer block to reverse the integral of velocity. Experiments show that this interesting property holds for two geophysics inversion problems over four different datasets. Compared to much deeper InversionNet~\cite{wu2019inversionnet}, our method achieves comparable accuracy, but consumes significantly fewer parameters.

Exploring Multi-physics with Extremely Weak Supervision

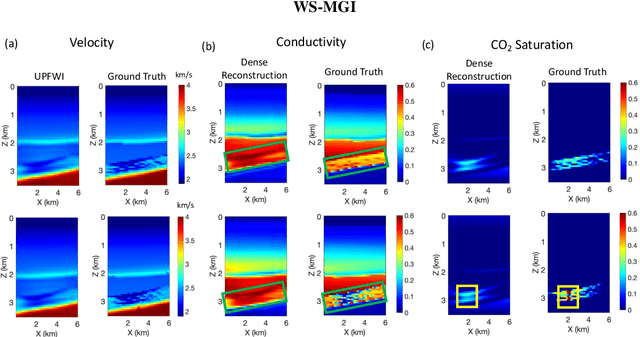
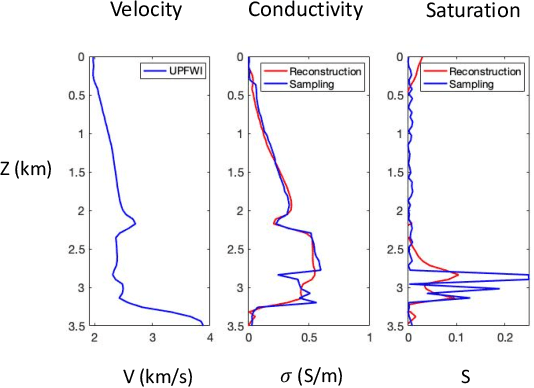
Multi-physical inversion plays a critical role in geophysics. It has been widely used to infer various physical properties (such as velocity and conductivity), simultaneously. Among those inversion problems, some are explicitly governed by partial differential equations (PDEs), while others are not. Without explicit governing equations, conventional multi-physical inversion techniques will not be feasible and data-driven inversion require expensive full labels. To overcome this issue, we develop a new data-driven multi-physics inversion technique with extremely weak supervision. Our key finding is that the pseudo labels can be constructed by learning the local relationship among geophysical properties at very sparse locations. We explore a multi-physics inversion problem from two distinct measurements (seismic and EM data) to three geophysical properties (velocity, conductivity, and CO$_2$ saturation). Our results show that we are able to invert for properties without explicit governing equations. Moreover, the label data on three geophysical properties can be significantly reduced by 50 times (from 100 down to only 2 locations).

OpenFWI: Benchmark Seismic Datasets for Machine Learning-Based Full Waveform Inversion

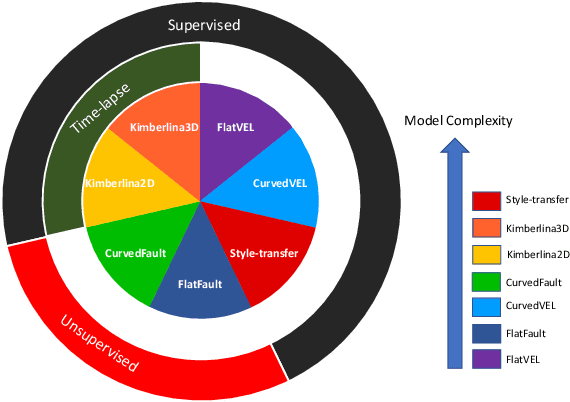
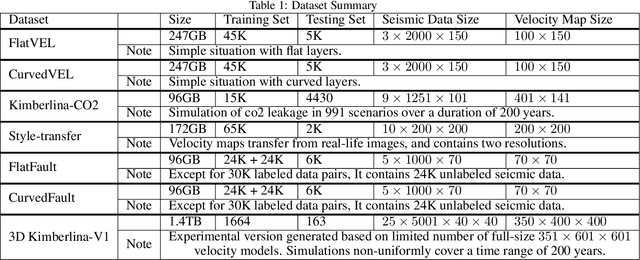
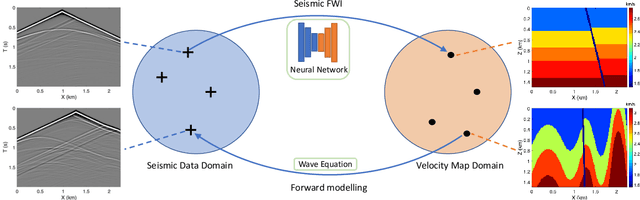
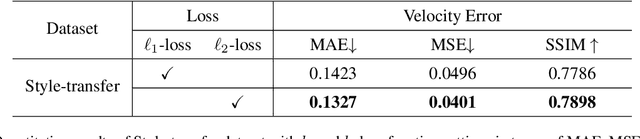
We present OpenFWI, a collection of large-scale open-source benchmark datasets for seismic full waveform inversion (FWI). OpenFWI is the first-of-its-kind in the geoscience and machine learning community to facilitate diversified, rigorous, and reproducible research on machine learning-based FWI. OpenFWI includes datasets of multiple scales, encompasses diverse domains, and covers various levels of model complexity. Along with the dataset, we also perform an empirical study on each dataset with a fully-convolutional deep learning model. OpenFWI has been meticulously maintained and will be regularly updated with new data and experimental results. We appreciate the inputs from the community to help us further improve OpenFWI. At the current version, we publish seven datasets in OpenFWI, of which one is specified for 3D FWI and the rest are for 2D scenarios. All datasets and related information can be accessed through our website at https://openfwi.github.io/.

Connect the Dots: In Situ 4D Seismic Monitoring of CO$_2$ Storage with Spatio-temporal CNNs

4D seismic imaging has been widely used in CO$_2$ sequestration projects to monitor the fluid flow in the volumetric subsurface region that is not sampled by wells. Ideally, real-time monitoring and near-future forecasting would provide site operators with great insights to understand the dynamics of the subsurface reservoir and assess any potential risks. However, due to obstacles such as high deployment cost, availability of acquisition equipment, exclusion zones around surface structures, only very sparse seismic imaging data can be obtained during monitoring. That leads to an unavoidable and growing knowledge gap over time. The operator needs to understand the fluid flow throughout the project lifetime and the seismic data are only available at a limited number of times, this is insufficient for understanding the reservoir behavior. To overcome those challenges, we have developed spatio-temporal neural-network-based models that can produce high-fidelity interpolated or extrapolated images effectively and efficiently. Specifically, our models are built on an autoencoder, and incorporate the long short-term memory (LSTM) structure with a new loss function regularized by optical flow. We validate the performance of our models using real 4D post-stack seismic imaging data acquired at the Sleipner CO$_2$ sequestration field. We employ two different strategies in evaluating our models. Numerically, we compare our models with different baseline approaches using classic pixel-based metrics. We also conduct a blind survey and collect a total of 20 responses from domain experts to evaluate the quality of data generated by our models. Via both numerical and expert evaluation, we conclude that our models can produce high-quality 2D/3D seismic imaging data at a reasonable cost, offering the possibility of real-time monitoring or even near-future forecasting of the CO$_2$ storage reservoir.