An Intriguing Property of Geophysics Inversion

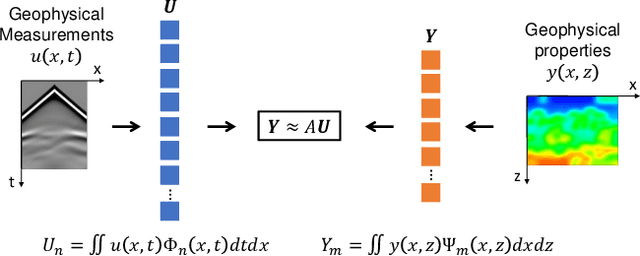
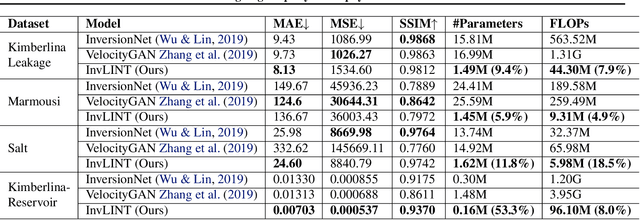
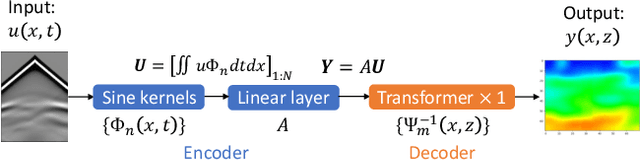
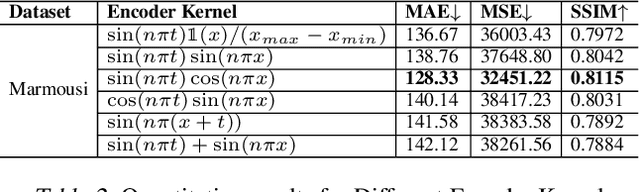
Inversion techniques are widely used to reconstruct subsurface physical properties (e.g., velocity, conductivity, and others) from surface-based geophysical measurements (e.g., seismic, electric/magnetic (EM) data). The problems are governed by partial differential equations~(PDEs) like the wave or Maxwell's equations. Solving geophysical inversion problems is challenging due to the ill-posedness and high computational cost. To alleviate those issues, recent studies leverage deep neural networks to learn the inversion mappings from geophysical measurements to the geophysical property directly. In this paper, we show that such a mapping can be well modeled by a \textit{very shallow}~(but not wide) network with only five layers. This is achieved based on our new finding of an intriguing property: \textit{a near-linear relationship between the input and output, after applying integral transform in high dimensional space.} In particular, when dealing with the inversion from seismic data to subsurface velocity governed by a wave equation, the integral results of velocity with Gaussian kernels are linearly correlated to the integral of seismic data with sine kernels. Furthermore, this property can be easily turned into a light-weight encoder-decoder network for inversion. The encoder contains the integration of seismic data and the linear transformation without need for fine-tuning. The decoder only consists of a single transformer block to reverse the integral of velocity. Experiments show that this interesting property holds for two geophysics inversion problems over four different datasets. Compared to much deeper InversionNet~\cite{wu2019inversionnet}, our method achieves comparable accuracy, but consumes significantly fewer parameters.