On the Price of Differential Privacy for Hierarchical Clustering

Hierarchical clustering is a fundamental unsupervised machine learning task with the aim of organizing data into a hierarchy of clusters. Many applications of hierarchical clustering involve sensitive user information, therefore motivating recent studies on differentially private hierarchical clustering under the rigorous framework of Dasgupta's objective. However, it has been shown that any privacy-preserving algorithm under edge-level differential privacy necessarily suffers a large error. To capture practical applications of this problem, we focus on the weight privacy model, where each edge of the input graph is at least unit weight. We present a novel algorithm in the weight privacy model that shows significantly better approximation than known impossibility results in the edge-level DP setting. In particular, our algorithm achieves $O(\log^{1.5}n/\varepsilon)$ multiplicative error for $\varepsilon$-DP and runs in polynomial time, where $n$ is the size of the input graph, and the cost is never worse than the optimal additive error in existing work. We complement our algorithm by showing if the unit-weight constraint does not apply, the lower bound for weight-level DP hierarchical clustering is essentially the same as the edge-level DP, i.e. $\Omega(n^2/\varepsilon)$ additive error. As a result, we also obtain a new lower bound of $\tilde{\Omega}(1/\varepsilon)$ additive error for balanced sparsest cuts in the weight-level DP model, which may be of independent interest. Finally, we evaluate our algorithm on synthetic and real-world datasets. Our experimental results show that our algorithm performs well in terms of extra cost and has good scalability to large graphs.

Neuc-MDS: Non-Euclidean Multidimensional Scaling Through Bilinear Forms

We introduce Non-Euclidean-MDS (Neuc-MDS), an extension of classical Multidimensional Scaling (MDS) that accommodates non-Euclidean and non-metric inputs. The main idea is to generalize the standard inner product to symmetric bilinear forms to utilize the negative eigenvalues of dissimilarity Gram matrices. Neuc-MDS efficiently optimizes the choice of (both positive and negative) eigenvalues of the dissimilarity Gram matrix to reduce STRESS, the sum of squared pairwise error. We provide an in-depth error analysis and proofs of the optimality in minimizing lower bounds of STRESS. We demonstrate Neuc-MDS's ability to address limitations of classical MDS raised by prior research, and test it on various synthetic and real-world datasets in comparison with both linear and non-linear dimension reduction methods.

RIO-CPD: A Riemannian Geometric Method for Correlation-aware Online Change Point Detection

The objective of change point detection is to identify abrupt changes at potentially multiple points within a data sequence. This task is particularly challenging in the online setting where various types of changes can occur, including shifts in both the marginal and joint distributions of the data. This paper tackles these challenges by sequentially tracking correlation matrices on the Riemannian geometry, where the geodesic distances accurately capture the development of correlations. We propose Rio-CPD, a non-parametric correlation-aware online change point detection framework that combines the Riemannian geometry of the manifold of symmetric positive definite matrices and the cumulative sum statistic (CUSUM) for detecting change points. Rio-CPD enhances CUSUM by computing the geodesic distance from present observations to the Fr\'echet mean of previous observations. With careful choice of metrics equipped to the Riemannian geometry, Rio-CPD is simple and computationally efficient. Experimental results on both synthetic and real-world datasets demonstrate that Rio-CPD outperforms existing methods in detection accuracy and efficiency.

Deconstructing The Ethics of Large Language Models from Long-standing Issues to New-emerging Dilemmas

Large Language Models (LLMs) have achieved unparalleled success across diverse language modeling tasks in recent years. However, this progress has also intensified ethical concerns, impacting the deployment of LLMs in everyday contexts. This paper provides a comprehensive survey of ethical challenges associated with LLMs, from longstanding issues such as copyright infringement, systematic bias, and data privacy, to emerging problems like truthfulness and social norms. We critically analyze existing research aimed at understanding, examining, and mitigating these ethical risks. Our survey underscores integrating ethical standards and societal values into the development of LLMs, thereby guiding the development of responsible and ethically aligned language models.

LEMMA-RCA: A Large Multi-modal Multi-domain Dataset for Root Cause Analysis

Root cause analysis (RCA) is crucial for enhancing the reliability and performance of complex systems. However, progress in this field has been hindered by the lack of large-scale, open-source datasets tailored for RCA. To bridge this gap, we introduce LEMMA-RCA, a large dataset designed for diverse RCA tasks across multiple domains and modalities. LEMMA-RCA features various real-world fault scenarios from IT and OT operation systems, encompassing microservices, water distribution, and water treatment systems, with hundreds of system entities involved. We evaluate the quality of LEMMA-RCA by testing the performance of eight baseline methods on this dataset under various settings, including offline and online modes as well as single and multiple modalities. Our experimental results demonstrate the high quality of LEMMA-RCA. The dataset is publicly available at https://lemma-rca.github.io/.

$\mathbf{\mathbb{E}^{FWI}}$: Multi-parameter Benchmark Datasets for Elastic Full Waveform Inversion of Geophysical Properties

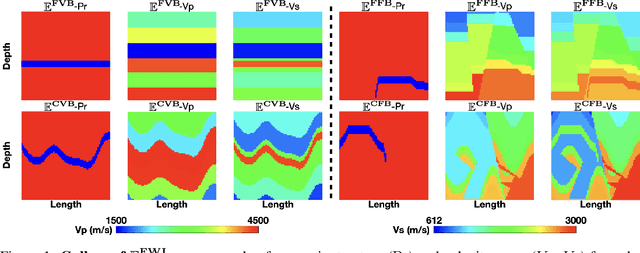
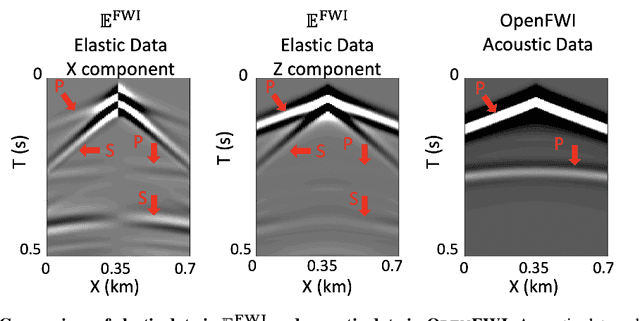
Elastic geophysical properties (such as P- and S-wave velocities) are of great importance to various subsurface applications like CO$_2$ sequestration and energy exploration (e.g., hydrogen and geothermal). Elastic full waveform inversion (FWI) is widely applied for characterizing reservoir properties. In this paper, we introduce $\mathbf{\mathbb{E}^{FWI}}$, a comprehensive benchmark dataset that is specifically designed for elastic FWI. $\mathbf{\mathbb{E}^{FWI}}$ encompasses 8 distinct datasets that cover diverse subsurface geologic structures (flat, curve, faults, etc). The benchmark results produced by three different deep learning methods are provided. In contrast to our previously presented dataset (pressure recordings) for acoustic FWI (referred to as OpenFWI), the seismic dataset in $\mathbf{\mathbb{E}^{FWI}}$ has both vertical and horizontal components. Moreover, the velocity maps in $\mathbf{\mathbb{E}^{FWI}}$ incorporate both P- and S-wave velocities. While the multicomponent data and the added S-wave velocity make the data more realistic, more challenges are introduced regarding the convergence and computational cost of the inversion. We conduct comprehensive numerical experiments to explore the relationship between P-wave and S-wave velocities in seismic data. The relation between P- and S-wave velocities provides crucial insights into the subsurface properties such as lithology, porosity, fluid content, etc. We anticipate that $\mathbf{\mathbb{E}^{FWI}}$ will facilitate future research on multiparameter inversions and stimulate endeavors in several critical research topics of carbon-zero and new energy exploration. All datasets, codes and relevant information can be accessed through our website at https://efwi-lanl.github.io/

Beyond One-Model-Fits-All: A Survey of Domain Specialization for Large Language Models

Large language models (LLMs) have significantly advanced the field of natural language processing (NLP), providing a highly useful, task-agnostic foundation for a wide range of applications. The great promise of LLMs as general task solvers motivated people to extend their functionality largely beyond just a ``chatbot'', and use it as an assistant or even replacement for domain experts and tools in specific domains such as healthcare, finance, and education. However, directly applying LLMs to solve sophisticated problems in specific domains meets many hurdles, caused by the heterogeneity of domain data, the sophistication of domain knowledge, the uniqueness of domain objectives, and the diversity of the constraints (e.g., various social norms, cultural conformity, religious beliefs, and ethical standards in the domain applications). To fill such a gap, explosively-increase research, and practices have been conducted in very recent years on the domain specialization of LLMs, which, however, calls for a comprehensive and systematic review to better summarizes and guide this promising domain. In this survey paper, first, we propose a systematic taxonomy that categorizes the LLM domain-specialization techniques based on the accessibility to LLMs and summarizes the framework for all the subcategories as well as their relations and differences to each other. We also present a comprehensive taxonomy of critical application domains that can benefit from specialized LLMs, discussing their practical significance and open challenges. Furthermore, we offer insights into the current research status and future trends in this area.

Impossibility of Depth Reduction in Explainable Clustering

Over the last few years Explainable Clustering has gathered a lot of attention. Dasgupta et al. [ICML'20] initiated the study of explainable k-means and k-median clustering problems where the explanation is captured by a threshold decision tree which partitions the space at each node using axis parallel hyperplanes. Recently, Laber et al. [Pattern Recognition'23] made a case to consider the depth of the decision tree as an additional complexity measure of interest. In this work, we prove that even when the input points are in the Euclidean plane, then any depth reduction in the explanation incurs unbounded loss in the k-means and k-median cost. Formally, we show that there exists a data set X in the Euclidean plane, for which there is a decision tree of depth k-1 whose k-means/k-median cost matches the optimal clustering cost of X, but every decision tree of depth less than k-1 has unbounded cost w.r.t. the optimal cost of clustering. We extend our results to the k-center objective as well, albeit with weaker guarantees.

On the Robustness and Generalization of Deep Learning Driven Full Waveform Inversion

The data-driven approach has been demonstrated as a promising technique to solve complicated scientific problems. Full Waveform Inversion (FWI) is commonly epitomized as an image-to-image translation task, which motivates the use of deep neural networks as an end-to-end solution. Despite being trained with synthetic data, the deep learning-driven FWI is expected to perform well when evaluated with sufficient real-world data. In this paper, we study such properties by asking: how robust are these deep neural networks and how do they generalize? For robustness, we prove the upper bounds of the deviation between the predictions from clean and noisy data. Moreover, we demonstrate an interplay between the noise level and the additional gain of loss. For generalization, we prove a norm-based generalization error upper bound via a stability-generalization framework. Experimental results on seismic FWI datasets corroborate with the theoretical results, shedding light on a better understanding of utilizing Deep Learning for complicated scientific applications.

OpenFWI: Benchmark Seismic Datasets for Machine Learning-Based Full Waveform Inversion

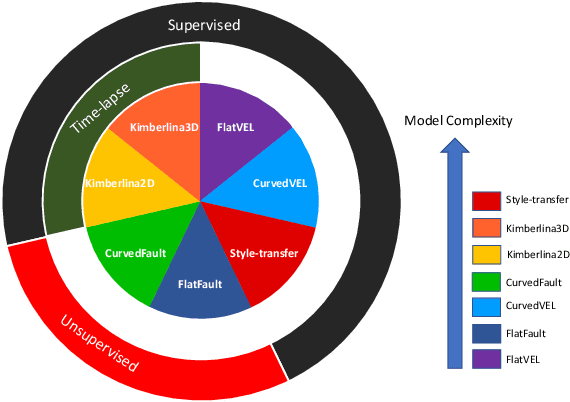
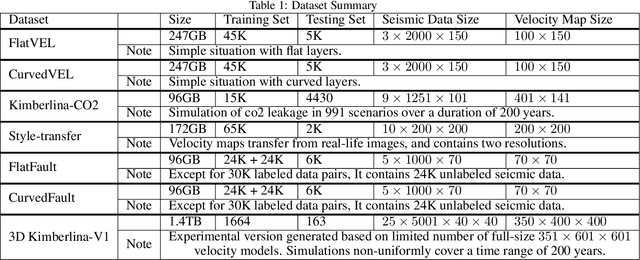
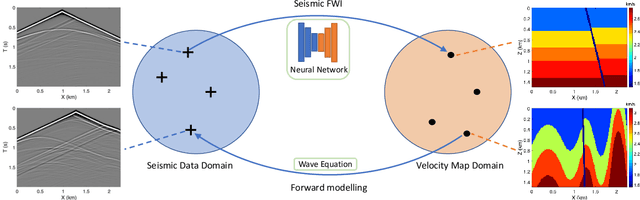
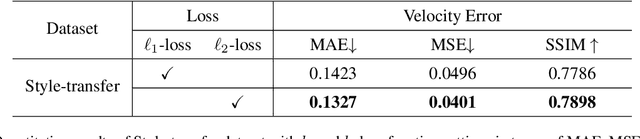
We present OpenFWI, a collection of large-scale open-source benchmark datasets for seismic full waveform inversion (FWI). OpenFWI is the first-of-its-kind in the geoscience and machine learning community to facilitate diversified, rigorous, and reproducible research on machine learning-based FWI. OpenFWI includes datasets of multiple scales, encompasses diverse domains, and covers various levels of model complexity. Along with the dataset, we also perform an empirical study on each dataset with a fully-convolutional deep learning model. OpenFWI has been meticulously maintained and will be regularly updated with new data and experimental results. We appreciate the inputs from the community to help us further improve OpenFWI. At the current version, we publish seven datasets in OpenFWI, of which one is specified for 3D FWI and the rest are for 2D scenarios. All datasets and related information can be accessed through our website at https://openfwi.github.io/.