Jalaj Upadhyay
Normalized Square Root: Sharper Matrix Factorization Bounds for Differentially Private Continual Counting
Sep 17, 2025Abstract:The factorization norms of the lower-triangular all-ones $n \times n$ matrix, $\gamma_2(M_{count})$ and $\gamma_{F}(M_{count})$, play a central role in differential privacy as they are used to give theoretical justification of the accuracy of the only known production-level private training algorithm of deep neural networks by Google. Prior to this work, the best known upper bound on $\gamma_2(M_{count})$ was $1 + \frac{\log n}{\pi}$ by Mathias (Linear Algebra and Applications, 1993), and the best known lower bound was $\frac{1}{\pi}(2 + \log(\frac{2n+1}{3})) \approx 0.507 + \frac{\log n}{\pi}$ (Matou\v{s}ek, Nikolov, Talwar, IMRN 2020), where $\log$ denotes the natural logarithm. Recently, Henzinger and Upadhyay (SODA 2025) gave the first explicit factorization that meets the bound of Mathias (1993) and asked whether there exists an explicit factorization that improves on Mathias' bound. We answer this question in the affirmative. Additionally, we improve the lower bound significantly. More specifically, we show that $$ 0.701 + \frac{\log n}{\pi} + o(1) \;\leq\; \gamma_2(M_{count}) \;\leq\; 0.846 + \frac{\log n}{\pi} + o(1). $$ That is, we reduce the gap between the upper and lower bound to $0.14 + o(1)$. We also show that our factors achieve a better upper bound for $\gamma_{F}(M_{count})$ compared to prior work, and we establish an improved lower bound: $$ 0.701 + \frac{\log n}{\pi} + o(1) \;\leq\; \gamma_{F}(M_{count}) \;\leq\; 0.748 + \frac{\log n}{\pi} + o(1). $$ That is, the gap between the lower and upper bound provided by our explicit factorization is $0.047 + o(1)$.
Correlated Noise Mechanisms for Differentially Private Learning
Jun 09, 2025
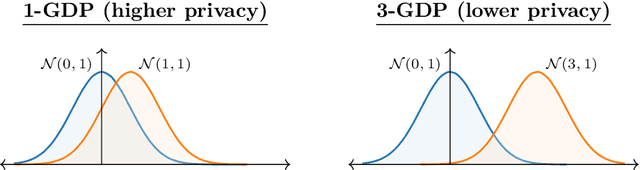

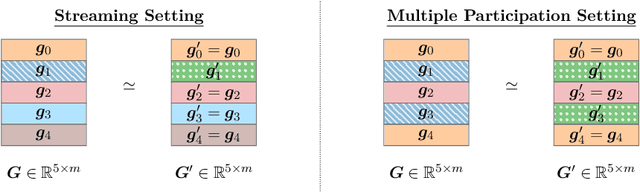
Abstract:This monograph explores the design and analysis of correlated noise mechanisms for differential privacy (DP), focusing on their application to private training of AI and machine learning models via the core primitive of estimation of weighted prefix sums. While typical DP mechanisms inject independent noise into each step of a stochastic gradient (SGD) learning algorithm in order to protect the privacy of the training data, a growing body of recent research demonstrates that introducing (anti-)correlations in the noise can significantly improve privacy-utility trade-offs by carefully canceling out some of the noise added on earlier steps in subsequent steps. Such correlated noise mechanisms, known variously as matrix mechanisms, factorization mechanisms, and DP-Follow-the-Regularized-Leader (DP-FTRL) when applied to learning algorithms, have also been influential in practice, with industrial deployment at a global scale.
Back to Square Roots: An Optimal Bound on the Matrix Factorization Error for Multi-Epoch Differentially Private SGD
May 17, 2025Abstract:Matrix factorization mechanisms for differentially private training have emerged as a promising approach to improve model utility under privacy constraints. In practical settings, models are typically trained over multiple epochs, requiring matrix factorizations that account for repeated participation. Existing theoretical upper and lower bounds on multi-epoch factorization error leave a significant gap. In this work, we introduce a new explicit factorization method, Banded Inverse Square Root (BISR), which imposes a banded structure on the inverse correlation matrix. This factorization enables us to derive an explicit and tight characterization of the multi-epoch error. We further prove that BISR achieves asymptotically optimal error by matching the upper and lower bounds. Empirically, BISR performs on par with state-of-the-art factorization methods, while being simpler to implement, computationally efficient, and easier to analyze.
On the Price of Differential Privacy for Hierarchical Clustering
Apr 22, 2025Abstract:Hierarchical clustering is a fundamental unsupervised machine learning task with the aim of organizing data into a hierarchy of clusters. Many applications of hierarchical clustering involve sensitive user information, therefore motivating recent studies on differentially private hierarchical clustering under the rigorous framework of Dasgupta's objective. However, it has been shown that any privacy-preserving algorithm under edge-level differential privacy necessarily suffers a large error. To capture practical applications of this problem, we focus on the weight privacy model, where each edge of the input graph is at least unit weight. We present a novel algorithm in the weight privacy model that shows significantly better approximation than known impossibility results in the edge-level DP setting. In particular, our algorithm achieves $O(\log^{1.5}n/\varepsilon)$ multiplicative error for $\varepsilon$-DP and runs in polynomial time, where $n$ is the size of the input graph, and the cost is never worse than the optimal additive error in existing work. We complement our algorithm by showing if the unit-weight constraint does not apply, the lower bound for weight-level DP hierarchical clustering is essentially the same as the edge-level DP, i.e. $\Omega(n^2/\varepsilon)$ additive error. As a result, we also obtain a new lower bound of $\tilde{\Omega}(1/\varepsilon)$ additive error for balanced sparsest cuts in the weight-level DP model, which may be of independent interest. Finally, we evaluate our algorithm on synthetic and real-world datasets. Our experimental results show that our algorithm performs well in terms of extra cost and has good scalability to large graphs.
Binned Group Algebra Factorization for Differentially Private Continual Counting
Apr 06, 2025Abstract:We study memory-efficient matrix factorization for differentially private counting under continual observation. While recent work by Henzinger and Upadhyay 2024 introduced a factorization method with reduced error based on group algebra, its practicality in streaming settings remains limited by computational constraints. We present new structural properties of the group algebra factorization, enabling the use of a binning technique from Andersson and Pagh (2024). By grouping similar values in rows, the binning method reduces memory usage and running time to $\tilde O(\sqrt{n})$, where $n$ is the length of the input stream, while maintaining a low error. Our work bridges the gap between theoretical improvements in factorization accuracy and practical efficiency in large-scale private learning systems.
Continual Release Moment Estimation with Differential Privacy
Feb 10, 2025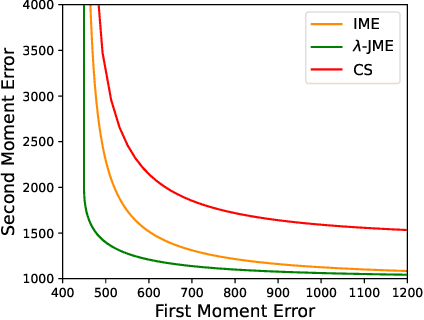
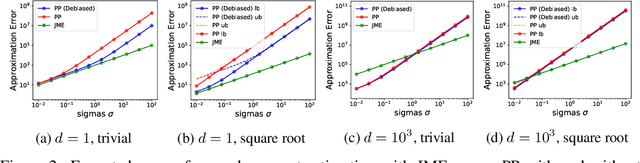

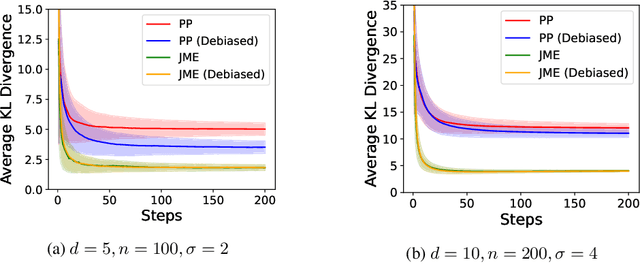
Abstract:We propose Joint Moment Estimation (JME), a method for continually and privately estimating both the first and second moments of data with reduced noise compared to naive approaches. JME uses the matrix mechanism and a joint sensitivity analysis to allow the second moment estimation with no additional privacy cost, thereby improving accuracy while maintaining privacy. We demonstrate JME's effectiveness in two applications: estimating the running mean and covariance matrix for Gaussian density estimation, and model training with DP-Adam on CIFAR-10.
Almost linear time differentially private release of synthetic graphs
Jun 04, 2024



Abstract:In this paper, we give an almost linear time and space algorithms to sample from an exponential mechanism with an $\ell_1$-score function defined over an exponentially large non-convex set. As a direct result, on input an $n$ vertex $m$ edges graph $G$, we present the \textit{first} $\widetilde{O}(m)$ time and $O(m)$ space algorithms for differentially privately outputting an $n$ vertex $O(m)$ edges synthetic graph that approximates all the cuts and the spectrum of $G$. These are the \emph{first} private algorithms for releasing synthetic graphs that nearly match this task's time and space complexity in the non-private setting while achieving the same (or better) utility as the previous works in the more practical sparse regime. Additionally, our algorithms can be extended to private graph analysis under continual observation.
Differentially Private Decentralized Learning with Random Walks
Feb 12, 2024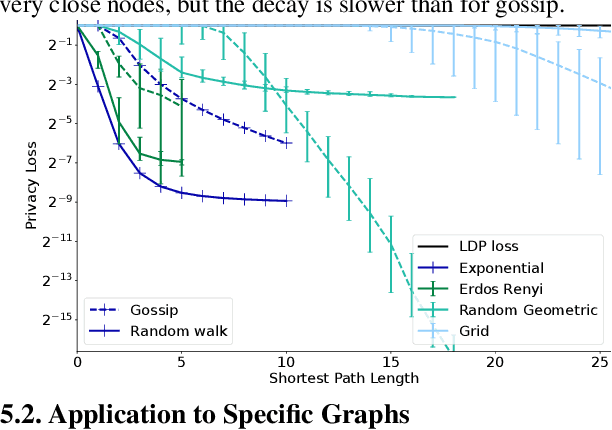
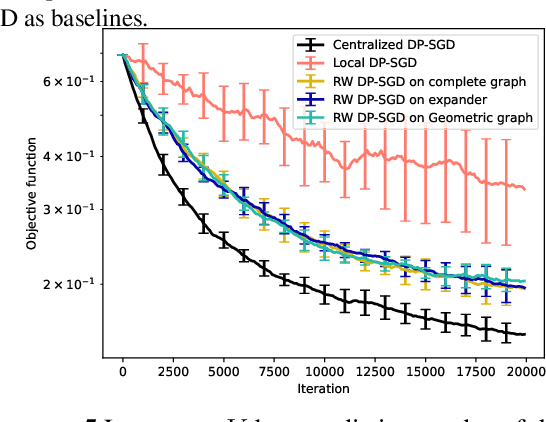
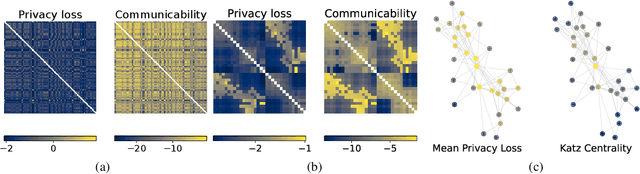
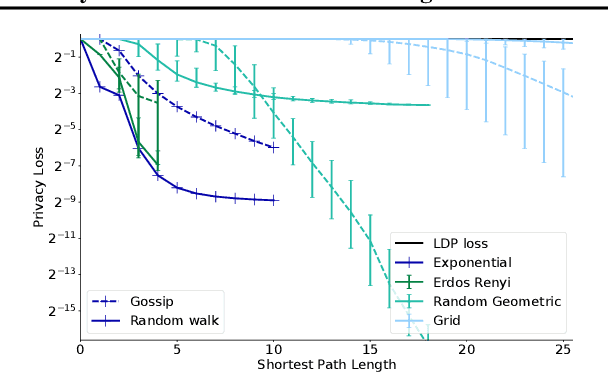
Abstract:The popularity of federated learning comes from the possibility of better scalability and the ability for participants to keep control of their data, improving data security and sovereignty. Unfortunately, sharing model updates also creates a new privacy attack surface. In this work, we characterize the privacy guarantees of decentralized learning with random walk algorithms, where a model is updated by traveling from one node to another along the edges of a communication graph. Using a recent variant of differential privacy tailored to the study of decentralized algorithms, namely Pairwise Network Differential Privacy, we derive closed-form expressions for the privacy loss between each pair of nodes where the impact of the communication topology is captured by graph theoretic quantities. Our results further reveal that random walk algorithms tends to yield better privacy guarantees than gossip algorithms for nodes close from each other. We supplement our theoretical results with empirical evaluation on synthetic and real-world graphs and datasets.
A Unifying Framework for Differentially Private Sums under Continual Observation
Jul 18, 2023
Abstract:We study the problem of maintaining a differentially private decaying sum under continual observation. We give a unifying framework and an efficient algorithm for this problem for \emph{any sufficiently smooth} function. Our algorithm is the first differentially private algorithm that does not have a multiplicative error for polynomially-decaying weights. Our algorithm improves on all prior works on differentially private decaying sums under continual observation and recovers exactly the additive error for the special case of continual counting from Henzinger et al. (SODA 2023) as a corollary. Our algorithm is a variant of the factorization mechanism whose error depends on the $\gamma_2$ and $\gamma_F$ norm of the underlying matrix. We give a constructive proof for an almost exact upper bound on the $\gamma_2$ and $\gamma_F$ norm and an almost tight lower bound on the $\gamma_2$ norm for a large class of lower-triangular matrices. This is the first non-trivial lower bound for lower-triangular matrices whose non-zero entries are not all the same. It includes matrices for all continual decaying sums problems, resulting in an upper bound on the additive error of any differentially private decaying sums algorithm under continual observation. We also explore some implications of our result in discrepancy theory and operator algebra. Given the importance of the $\gamma_2$ norm in computer science and the extensive work in mathematics, we believe our result will have further applications.
Almost Tight Error Bounds on Differentially Private Continual Counting
Nov 09, 2022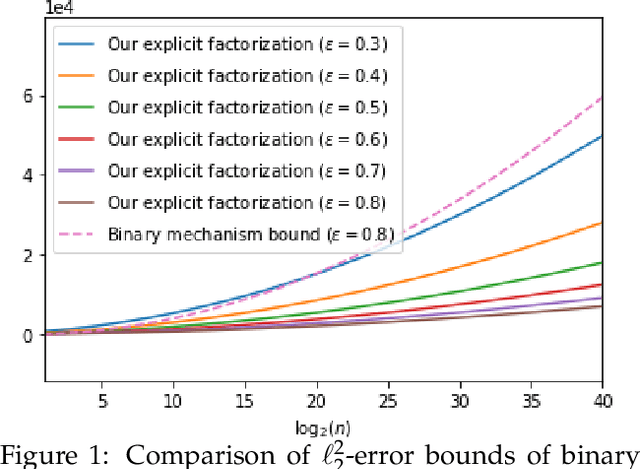
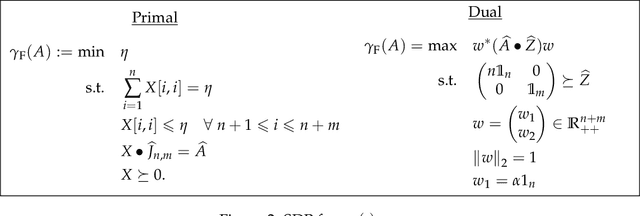
Abstract:The first large-scale deployment of private federated learning uses differentially private counting in the continual release model as a subroutine (Google AI blog titled "Federated Learning with Formal Differential Privacy Guarantees"). In this case, a concrete bound on the error is very relevant to reduce the privacy parameter. The standard mechanism for continual counting is the binary mechanism. We present a novel mechanism and show that its mean squared error is both asymptotically optimal and a factor 10 smaller than the error of the binary mechanism. We also show that the constants in our analysis are almost tight by giving non-asymptotic lower and upper bounds that differ only in the constants of lower-order terms. Our algorithm is a matrix mechanism for the counting matrix and takes constant time per release. We also use our explicit factorization of the counting matrix to give an upper bound on the excess risk of the private learning algorithm of Denisov et al. (NeurIPS 2022). Our lower bound for any continual counting mechanism is the first tight lower bound on continual counting under approximate differential privacy. It is achieved using a new lower bound on a certain factorization norm, denoted by $\gamma_F(\cdot)$, in terms of the singular values of the matrix. In particular, we show that for any complex matrix, $A \in \mathbb{C}^{m \times n}$, \[ \gamma_F(A) \geq \frac{1}{\sqrt{m}}\|A\|_1, \] where $\|\cdot \|$ denotes the Schatten-1 norm. We believe this technique will be useful in proving lower bounds for a larger class of linear queries. To illustrate the power of this technique, we show the first lower bound on the mean squared error for answering parity queries.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge