Continual Release Moment Estimation with Differential Privacy

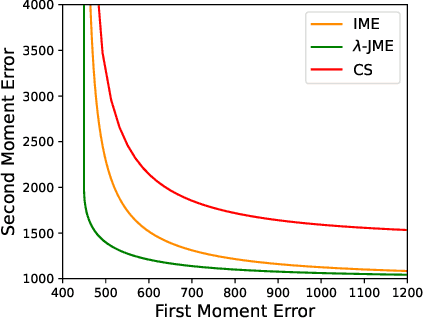
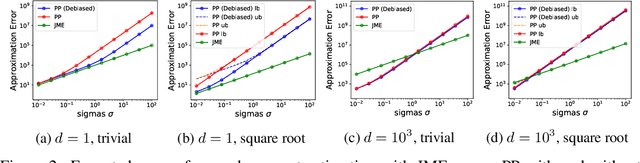
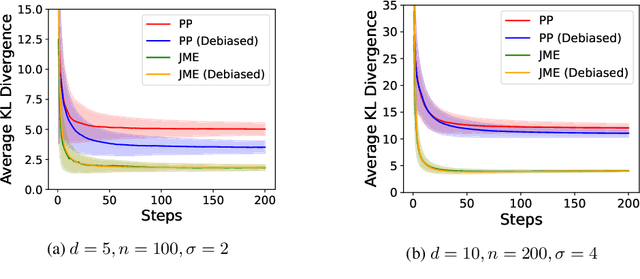
We propose Joint Moment Estimation (JME), a method for continually and privately estimating both the first and second moments of data with reduced noise compared to naive approaches. JME uses the matrix mechanism and a joint sensitivity analysis to allow the second moment estimation with no additional privacy cost, thereby improving accuracy while maintaining privacy. We demonstrate JME's effectiveness in two applications: estimating the running mean and covariance matrix for Gaussian density estimation, and model training with DP-Adam on CIFAR-10.

Notes on Sampled Gaussian Mechanism

In these notes, we prove a recent conjecture posed in the paper by R\"ais\"a, O. et al. [Subsampling is not Magic: Why Large Batch Sizes Work for Differentially Private Stochastic Optimization (2024)]. Theorem 6.2 of the paper asserts that for the Sampled Gaussian Mechanism - a composition of subsampling and additive Gaussian noise, the effective noise level, $\sigma_{\text{eff}} = \frac{\sigma(q)}{q}$, decreases as a function of the subsampling rate $q$. Consequently, larger subsampling rates are preferred for better privacy-utility trade-offs. Our notes provide a rigorous proof of Conjecture 6.3, which was left unresolved in the original paper, thereby completing the proof of Theorem 6.2.

DP-KAN: Differentially Private Kolmogorov-Arnold Networks

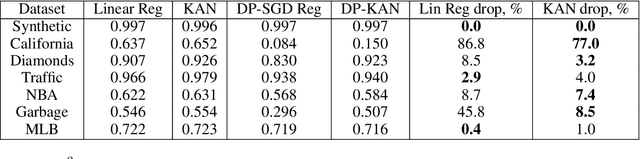
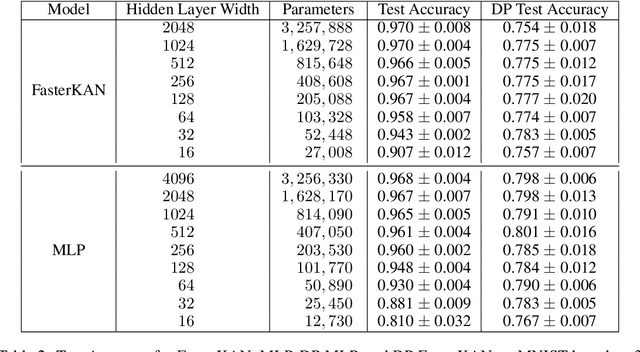
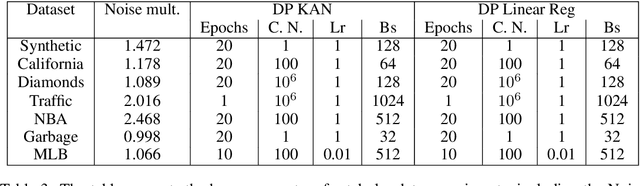
We study the Kolmogorov-Arnold Network (KAN), recently proposed as an alternative to the classical Multilayer Perceptron (MLP), in the application for differentially private model training. Using the DP-SGD algorithm, we demonstrate that KAN can be made private in a straightforward manner and evaluated its performance across several datasets. Our results indicate that the accuracy of KAN is not only comparable with MLP but also experiences similar deterioration due to privacy constraints, making it suitable for differentially private model training.