Simone Bombari
A Law of Data Reconstruction for Random Features (and Beyond)
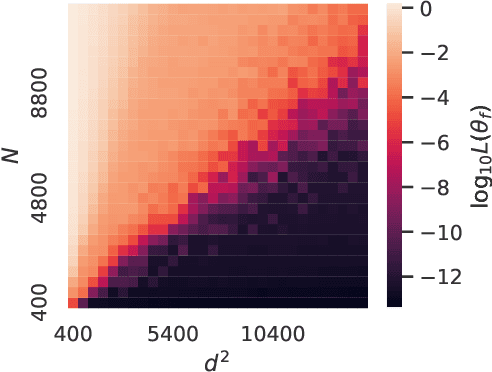
Sep 26, 2025Abstract:Large-scale deep learning models are known to memorize parts of the training set. In machine learning theory, memorization is often framed as interpolation or label fitting, and classical results show that this can be achieved when the number of parameters $p$ in the model is larger than the number of training samples $n$. In this work, we consider memorization from the perspective of data reconstruction, demonstrating that this can be achieved when $p$ is larger than $dn$, where $d$ is the dimensionality of the data. More specifically, we show that, in the random features model, when $p \gg dn$, the subspace spanned by the training samples in feature space gives sufficient information to identify the individual samples in input space. Our analysis suggests an optimization method to reconstruct the dataset from the model parameters, and we demonstrate that this method performs well on various architectures (random features, two-layer fully-connected and deep residual networks). Our results reveal a law of data reconstruction, according to which the entire training dataset can be recovered as $p$ exceeds the threshold $dn$.
Better Rates for Private Linear Regression in the Proportional Regime via Aggressive Clipping
May 22, 2025Abstract:Differentially private (DP) linear regression has received significant attention in the recent theoretical literature, with several works aimed at obtaining improved error rates. A common approach is to set the clipping constant much larger than the expected norm of the per-sample gradients. While simplifying the analysis, this is however in sharp contrast with what empirical evidence suggests to optimize performance. Our work bridges this gap between theory and practice: we provide sharper rates for DP stochastic gradient descent (DP-SGD) by crucially operating in a regime where clipping happens frequently. Specifically, we consider the setting where the data is multivariate Gaussian, the number of training samples $n$ is proportional to the input dimension $d$, and the algorithm guarantees constant-order zero concentrated DP. Our method relies on establishing a deterministic equivalent for the trajectory of DP-SGD in terms of a family of ordinary differential equations (ODEs). As a consequence, the risk of DP-SGD is bounded between two ODEs, with upper and lower bounds matching for isotropic data. By studying these ODEs when $n / d$ is large enough, we demonstrate the optimality of aggressive clipping, and we uncover the benefits of decaying learning rate and private noise scheduling.
Spurious Correlations in High Dimensional Regression: The Roles of Regularization, Simplicity Bias and Over-Parameterization
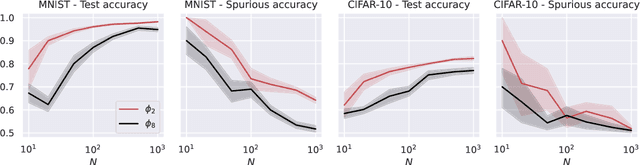
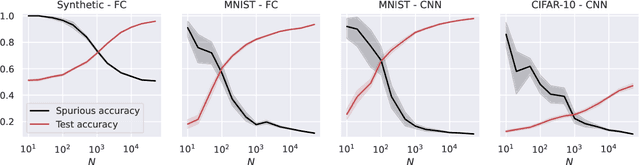
Feb 03, 2025Abstract:Learning models have been shown to rely on spurious correlations between non-predictive features and the associated labels in the training data, with negative implications on robustness, bias and fairness. In this work, we provide a statistical characterization of this phenomenon for high-dimensional regression, when the data contains a predictive core feature $x$ and a spurious feature $y$. Specifically, we quantify the amount of spurious correlations $C$ learned via linear regression, in terms of the data covariance and the strength $\lambda$ of the ridge regularization. As a consequence, we first capture the simplicity of $y$ through the spectrum of its covariance, and its correlation with $x$ through the Schur complement of the full data covariance. Next, we prove a trade-off between $C$ and the in-distribution test loss $L$, by showing that the value of $\lambda$ that minimizes $L$ lies in an interval where $C$ is increasing. Finally, we investigate the effects of over-parameterization via the random features model, by showing its equivalence to regularized linear regression. Our theoretical results are supported by numerical experiments on Gaussian, Color-MNIST, and CIFAR-10 datasets.
Privacy for Free in the Over-Parameterized Regime
Oct 18, 2024



Abstract:Differentially private gradient descent (DP-GD) is a popular algorithm to train deep learning models with provable guarantees on the privacy of the training data. In the last decade, the problem of understanding its performance cost with respect to standard GD has received remarkable attention from the research community, which formally derived upper bounds on the excess population risk $R_{P}$ in different learning settings. However, existing bounds typically degrade with over-parameterization, i.e., as the number of parameters $p$ gets larger than the number of training samples $n$ -- a regime which is ubiquitous in current deep-learning practice. As a result, the lack of theoretical insights leaves practitioners without clear guidance, leading some to reduce the effective number of trainable parameters to improve performance, while others use larger models to achieve better results through scale. In this work, we show that in the popular random features model with quadratic loss, for any sufficiently large $p$, privacy can be obtained for free, i.e., $\left|R_{P} \right| = o(1)$, not only when the privacy parameter $\varepsilon$ has constant order, but also in the strongly private setting $\varepsilon = o(1)$. This challenges the common wisdom that over-parameterization inherently hinders performance in private learning.
DP-KAN: Differentially Private Kolmogorov-Arnold Networks
Jul 17, 2024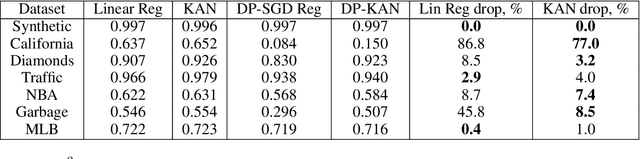

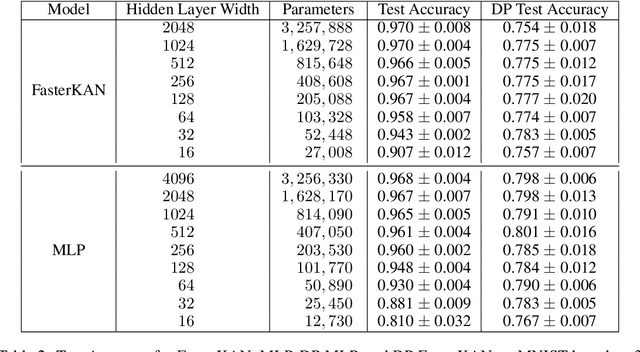
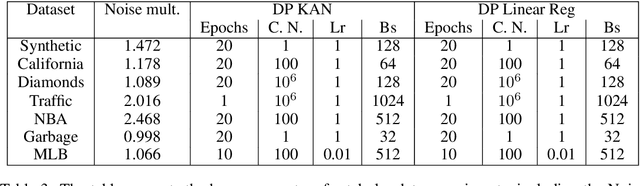
Abstract:We study the Kolmogorov-Arnold Network (KAN), recently proposed as an alternative to the classical Multilayer Perceptron (MLP), in the application for differentially private model training. Using the DP-SGD algorithm, we demonstrate that KAN can be made private in a straightforward manner and evaluated its performance across several datasets. Our results indicate that the accuracy of KAN is not only comparable with MLP but also experiences similar deterioration due to privacy constraints, making it suitable for differentially private model training.
Towards Understanding the Word Sensitivity of Attention Layers: A Study via Random Features
Feb 05, 2024Abstract:Unveiling the reasons behind the exceptional success of transformers requires a better understanding of why attention layers are suitable for NLP tasks. In particular, such tasks require predictive models to capture contextual meaning which often depends on one or few words, even if the sentence is long. Our work studies this key property, dubbed word sensitivity (WS), in the prototypical setting of random features. We show that attention layers enjoy high WS, namely, there exists a vector in the space of embeddings that largely perturbs the random attention features map. The argument critically exploits the role of the softmax in the attention layer, highlighting its benefit compared to other activations (e.g., ReLU). In contrast, the WS of standard random features is of order $1/\sqrt{n}$, $n$ being the number of words in the textual sample, and thus it decays with the length of the context. We then translate these results on the word sensitivity into generalization bounds: due to their low WS, random features provably cannot learn to distinguish between two sentences that differ only in a single word; in contrast, due to their high WS, random attention features have higher generalization capabilities. We validate our theoretical results with experimental evidence over the BERT-Base word embeddings of the imdb review dataset.
Stability, Generalization and Privacy: Precise Analysis for Random and NTK Features
May 20, 2023
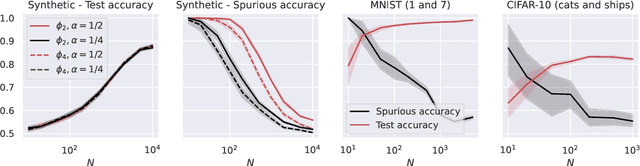
Abstract:Deep learning models can be vulnerable to recovery attacks, raising privacy concerns to users, and widespread algorithms such as empirical risk minimization (ERM) often do not directly enforce safety guarantees. In this paper, we study the safety of ERM-trained models against a family of powerful black-box attacks. Our analysis quantifies this safety via two separate terms: (i) the model stability with respect to individual training samples, and (ii) the feature alignment between the attacker query and the original data. While the first term is well established in learning theory and it is connected to the generalization error in classical work, the second one is, to the best of our knowledge, novel. Our key technical result provides a precise characterization of the feature alignment for the two prototypical settings of random features (RF) and neural tangent kernel (NTK) regression. This proves that privacy strengthens with an increase in the generalization capability, unveiling also the role of the activation function. Numerical experiments show a behavior in agreement with our theory not only for the RF and NTK models, but also for deep neural networks trained on standard datasets (MNIST, CIFAR-10).
Beyond the Universal Law of Robustness: Sharper Laws for Random Features and Neural Tangent Kernels
Feb 03, 2023Abstract:Machine learning models are vulnerable to adversarial perturbations, and a thought-provoking paper by Bubeck and Sellke has analyzed this phenomenon through the lens of over-parameterization: interpolating smoothly the data requires significantly more parameters than simply memorizing it. However, this "universal" law provides only a necessary condition for robustness, and it is unable to discriminate between models. In this paper, we address these gaps by focusing on empirical risk minimization in two prototypical settings, namely, random features and the neural tangent kernel (NTK). We prove that, for random features, the model is not robust for any degree of over-parameterization, even when the necessary condition coming from the universal law of robustness is satisfied. In contrast, for even activations, the NTK model meets the universal lower bound, and it is robust as soon as the necessary condition on over-parameterization is fulfilled. This also addresses a conjecture in prior work by Bubeck, Li and Nagaraj. Our analysis decouples the effect of the kernel of the model from an "interaction matrix", which describes the interaction with the test data and captures the effect of the activation. Our theoretical results are corroborated by numerical evidence on both synthetic and standard datasets (MNIST, CIFAR-10).
Memorization and Optimization in Deep Neural Networks with Minimum Over-parameterization
May 20, 2022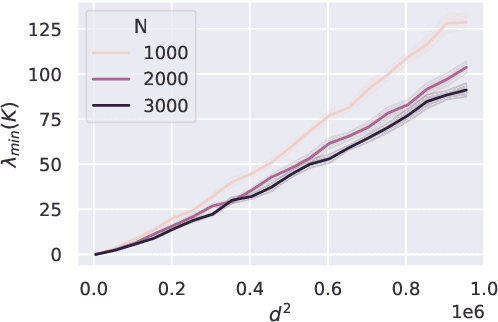
Abstract:The Neural Tangent Kernel (NTK) has emerged as a powerful tool to provide memorization, optimization and generalization guarantees in deep neural networks. A line of work has studied the NTK spectrum for two-layer and deep networks with at least a layer with $\Omega(N)$ neurons, $N$ being the number of training samples. Furthermore, there is increasing evidence suggesting that deep networks with sub-linear layer widths are powerful memorizers and optimizers, as long as the number of parameters exceeds the number of samples. Thus, a natural open question is whether the NTK is well conditioned in such a challenging sub-linear setup. In this paper, we answer this question in the affirmative. Our key technical contribution is a lower bound on the smallest NTK eigenvalue for deep networks with the minimum possible over-parameterization: the number of parameters is roughly $\Omega(N)$ and, hence, the number of neurons is as little as $\Omega(\sqrt{N})$. To showcase the applicability of our NTK bounds, we provide two results concerning memorization capacity and optimization guarantees for gradient descent training.
Sharp asymptotics on the compression of two-layer neural networks
May 18, 2022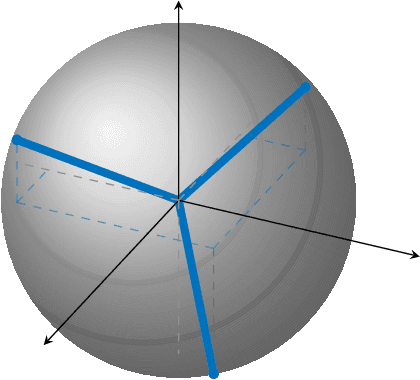
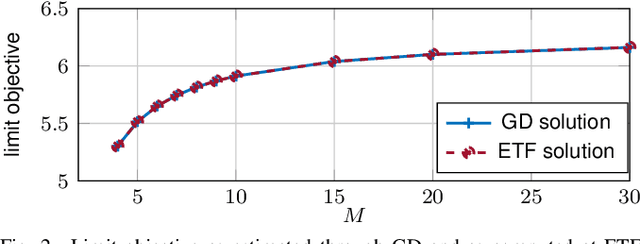
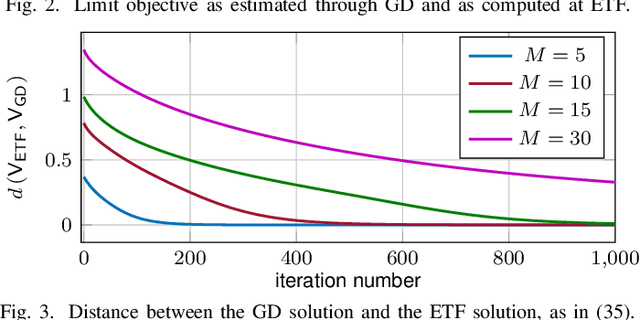
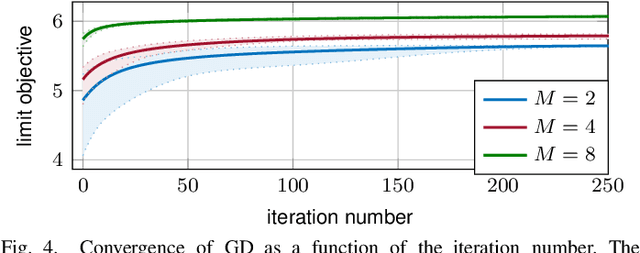
Abstract:In this paper, we study the compression of a target two-layer neural network with N nodes into a compressed network with M < N nodes. More precisely, we consider the setting in which the weights of the target network are i.i.d. sub-Gaussian, and we minimize the population L2 loss between the outputs of the target and of the compressed network, under the assumption of Gaussian inputs. By using tools from high-dimensional probability, we show that this non-convex problem can be simplified when the target network is sufficiently over-parameterized, and provide the error rate of this approximation as a function of the input dimension and N . For a ReLU activation function, we conjecture that the optimum of the simplified optimization problem is achieved by taking weights on the Equiangular Tight Frame (ETF), while the scaling of the weights and the orientation of the ETF depend on the parameters of the target network. Numerical evidence is provided to support this conjecture.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge