Exact Dynamics of Multi-class Stochastic Gradient Descent

We develop a framework for analyzing the training and learning rate dynamics on a variety of high- dimensional optimization problems trained using one-pass stochastic gradient descent (SGD) with data generated from multiple anisotropic classes. We give exact expressions for a large class of functions of the limiting dynamics, including the risk and the overlap with the true signal, in terms of a deterministic solution to a system of ODEs. We extend the existing theory of high-dimensional SGD dynamics to Gaussian-mixture data and a large (growing with the parameter size) number of classes. We then investigate in detail the effect of the anisotropic structure of the covariance of the data in the problems of binary logistic regression and least square loss. We study three cases: isotropic covariances, data covariance matrices with a large fraction of zero eigenvalues (denoted as the zero-one model), and covariance matrices with spectra following a power-law distribution. We show that there exists a structural phase transition. In particular, we demonstrate that, for the zero-one model and the power-law model with sufficiently large power, SGD tends to align more closely with values of the class mean that are projected onto the "clean directions" (i.e., directions of smaller variance). This is supported by both numerical simulations and analytical studies, which show the exact asymptotic behavior of the loss in the high-dimensional limit.

A Geometric Unification of Generative AI with Manifold-Probabilistic Projection Models

The foundational premise of generative AI for images is the assumption that images are inherently low-dimensional objects embedded within a high-dimensional space. Additionally, it is often implicitly assumed that thematic image datasets form smooth or piecewise smooth manifolds. Common approaches overlook the geometric structure and focus solely on probabilistic methods, approximating the probability distribution through universal approximation techniques such as the kernel method. In some generative models, the low dimensional nature of the data manifest itself by the introduction of a lower dimensional latent space. Yet, the probability distribution in the latent or the manifold coordinate space is considered uninteresting and is predefined or considered uniform. This study unifies the geometric and probabilistic perspectives by providing a geometric framework and a kernel-based probabilistic method simultaneously. The resulting framework demystifies diffusion models by interpreting them as a projection mechanism onto the manifold of ``good images''. This interpretation leads to the construction of a new deterministic model, the Manifold-Probabilistic Projection Model (MPPM), which operates in both the representation (pixel) space and the latent space. We demonstrate that the Latent MPPM (LMPPM) outperforms the Latent Diffusion Model (LDM) across various datasets, achieving superior results in terms of image restoration and generation.

Better Rates for Private Linear Regression in the Proportional Regime via Aggressive Clipping

Differentially private (DP) linear regression has received significant attention in the recent theoretical literature, with several works aimed at obtaining improved error rates. A common approach is to set the clipping constant much larger than the expected norm of the per-sample gradients. While simplifying the analysis, this is however in sharp contrast with what empirical evidence suggests to optimize performance. Our work bridges this gap between theory and practice: we provide sharper rates for DP stochastic gradient descent (DP-SGD) by crucially operating in a regime where clipping happens frequently. Specifically, we consider the setting where the data is multivariate Gaussian, the number of training samples $n$ is proportional to the input dimension $d$, and the algorithm guarantees constant-order zero concentrated DP. Our method relies on establishing a deterministic equivalent for the trajectory of DP-SGD in terms of a family of ordinary differential equations (ODEs). As a consequence, the risk of DP-SGD is bounded between two ODEs, with upper and lower bounds matching for isotropic data. By studying these ODEs when $n / d$ is large enough, we demonstrate the optimality of aggressive clipping, and we uncover the benefits of decaying learning rate and private noise scheduling.

Applications of Statistical Field Theory in Deep Learning

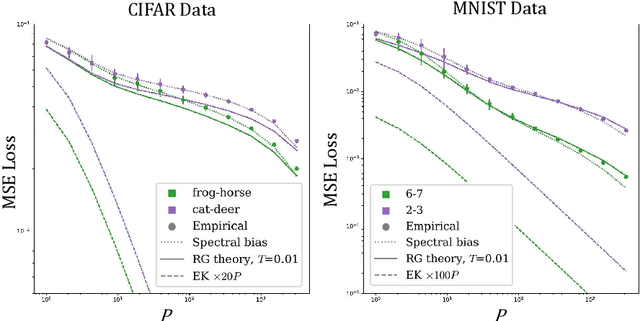
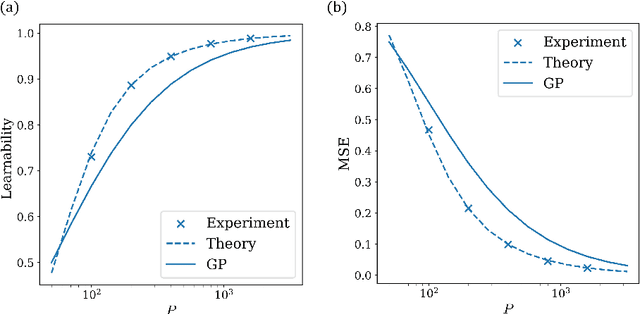
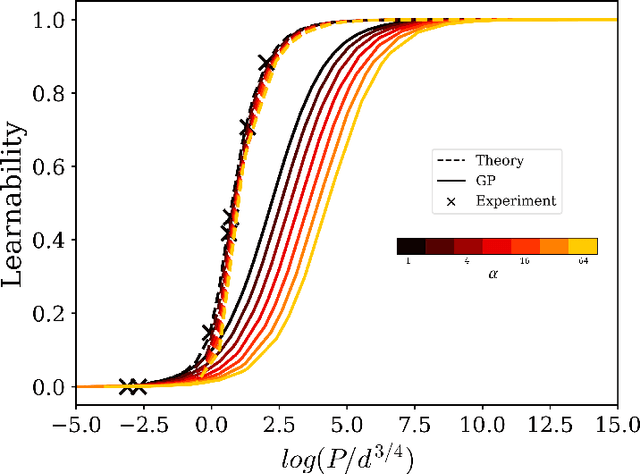
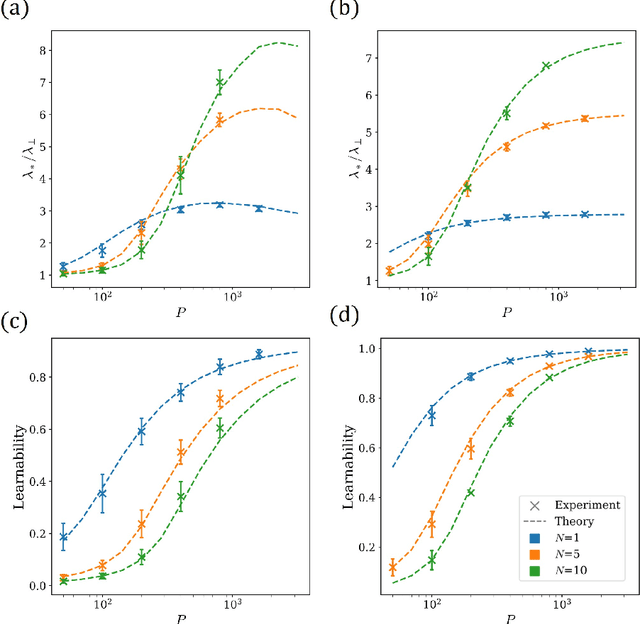
Deep learning algorithms have made incredible strides in the past decade yet due to the complexity of these algorithms, the science of deep learning remains in its early stages. Being an experimentally driven field, it is natural to seek a theory of deep learning within the physics paradigm. As deep learning is largely about learning functions and distributions over functions, statistical field theory, a rich and versatile toolbox for tackling complex distributions over functions (fields) is an obvious choice of formalism. Research efforts carried out in the past few years have demonstrated the ability of field theory to provide useful insights on generalization, implicit bias, and feature learning effects. Here we provide a pedagogical review of this emerging line of research.

From Kernels to Features: A Multi-Scale Adaptive Theory of Feature Learning

Theoretically describing feature learning in neural networks is crucial for understanding their expressive power and inductive biases, motivating various approaches. Some approaches describe network behavior after training through a simple change in kernel scale from initialization, resulting in a generalization power comparable to a Gaussian process. Conversely, in other approaches training results in the adaptation of the kernel to the data, involving complex directional changes to the kernel. While these approaches capture different facets of network behavior, their relationship and respective strengths across scaling regimes remains an open question. This work presents a theoretical framework of multi-scale adaptive feature learning bridging these approaches. Using methods from statistical mechanics, we derive analytical expressions for network output statistics which are valid across scaling regimes and in the continuum between them. A systematic expansion of the network's probability distribution reveals that mean-field scaling requires only a saddle-point approximation, while standard scaling necessitates additional correction terms. Remarkably, we find across regimes that kernel adaptation can be reduced to an effective kernel rescaling when predicting the mean network output of a linear network. However, even in this case, the multi-scale adaptive approach captures directional feature learning effects, providing richer insights than what could be recovered from a rescaling of the kernel alone.

The High Line: Exact Risk and Learning Rate Curves of Stochastic Adaptive Learning Rate Algorithms

We develop a framework for analyzing the training and learning rate dynamics on a large class of high-dimensional optimization problems, which we call the high line, trained using one-pass stochastic gradient descent (SGD) with adaptive learning rates. We give exact expressions for the risk and learning rate curves in terms of a deterministic solution to a system of ODEs. We then investigate in detail two adaptive learning rates -- an idealized exact line search and AdaGrad-Norm -- on the least squares problem. When the data covariance matrix has strictly positive eigenvalues, this idealized exact line search strategy can exhibit arbitrarily slower convergence when compared to the optimal fixed learning rate with SGD. Moreover we exactly characterize the limiting learning rate (as time goes to infinity) for line search in the setting where the data covariance has only two distinct eigenvalues. For noiseless targets, we further demonstrate that the AdaGrad-Norm learning rate converges to a deterministic constant inversely proportional to the average eigenvalue of the data covariance matrix, and identify a phase transition when the covariance density of eigenvalues follows a power law distribution.

Optimal minimax rate of learning interaction kernels

Nonparametric estimation of nonlocal interaction kernels is crucial in various applications involving interacting particle systems. The inference challenge, situated at the nexus of statistical learning and inverse problems, comes from the nonlocal dependency. A central question is whether the optimal minimax rate of convergence for this problem aligns with the rate of $M^{-\frac{2\beta}{2\beta+1}}$ in classical nonparametric regression, where $M$ is the sample size and $\beta$ represents the smoothness exponent of the radial kernel. Our study confirms this alignment for systems with a finite number of particles. We introduce a tamed least squares estimator (tLSE) that attains the optimal convergence rate for a broad class of exchangeable distributions. The tLSE bridges the smallest eigenvalue of random matrices and Sobolev embedding. This estimator relies on nonasymptotic estimates for the left tail probability of the smallest eigenvalue of the normal matrix. The lower minimax rate is derived using the Fano-Tsybakov hypothesis testing method. Our findings reveal that provided the inverse problem in the large sample limit satisfies a coercivity condition, the left tail probability does not alter the bias-variance tradeoff, and the optimal minimax rate remains intact. Our tLSE method offers a straightforward approach for establishing the optimal minimax rate for models with either local or nonlocal dependency.

Droplets of Good Representations: Grokking as a First Order Phase Transition in Two Layer Networks

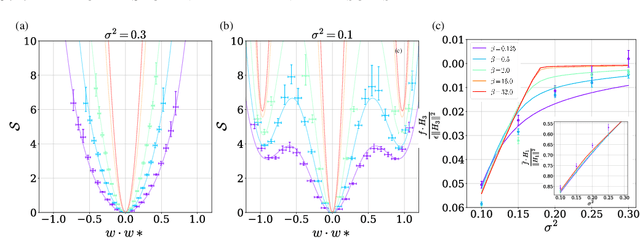
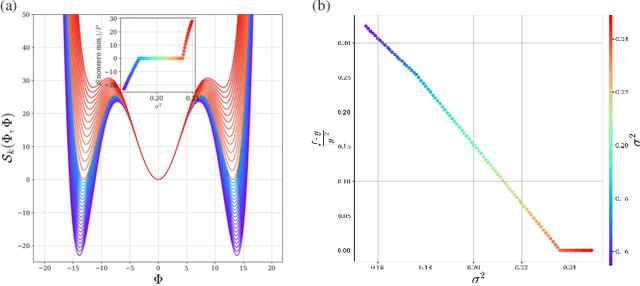
A key property of deep neural networks (DNNs) is their ability to learn new features during training. This intriguing aspect of deep learning stands out most clearly in recently reported Grokking phenomena. While mainly reflected as a sudden increase in test accuracy, Grokking is also believed to be a beyond lazy-learning/Gaussian Process (GP) phenomenon involving feature learning. Here we apply a recent development in the theory of feature learning, the adaptive kernel approach, to two teacher-student models with cubic-polynomial and modular addition teachers. We provide analytical predictions on feature learning and Grokking properties of these models and demonstrate a mapping between Grokking and the theory of phase transitions. We show that after Grokking, the state of the DNN is analogous to the mixed phase following a first-order phase transition. In this mixed phase, the DNN generates useful internal representations of the teacher that are sharply distinct from those before the transition.

Hitting the High-Dimensional Notes: An ODE for SGD learning dynamics on GLMs and multi-index models

We analyze the dynamics of streaming stochastic gradient descent (SGD) in the high-dimensional limit when applied to generalized linear models and multi-index models (e.g. logistic regression, phase retrieval) with general data-covariance. In particular, we demonstrate a deterministic equivalent of SGD in the form of a system of ordinary differential equations that describes a wide class of statistics, such as the risk and other measures of sub-optimality. This equivalence holds with overwhelming probability when the model parameter count grows proportionally to the number of data. This framework allows us to obtain learning rate thresholds for stability of SGD as well as convergence guarantees. In addition to the deterministic equivalent, we introduce an SDE with a simplified diffusion coefficient (homogenized SGD) which allows us to analyze the dynamics of general statistics of SGD iterates. Finally, we illustrate this theory on some standard examples and show numerical simulations which give an excellent match to the theory.

Speed Limits for Deep Learning

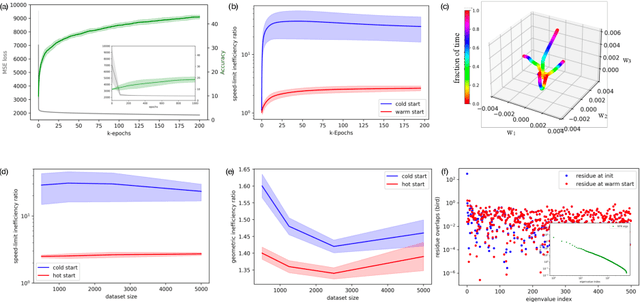
State-of-the-art neural networks require extreme computational power to train. It is therefore natural to wonder whether they are optimally trained. Here we apply a recent advancement in stochastic thermodynamics which allows bounding the speed at which one can go from the initial weight distribution to the final distribution of the fully trained network, based on the ratio of their Wasserstein-2 distance and the entropy production rate of the dynamical process connecting them. Considering both gradient-flow and Langevin training dynamics, we provide analytical expressions for these speed limits for linear and linearizable neural networks e.g. Neural Tangent Kernel (NTK). Remarkably, given some plausible scaling assumptions on the NTK spectra and spectral decomposition of the labels -- learning is optimal in a scaling sense. Our results are consistent with small-scale experiments with Convolutional Neural Networks (CNNs) and Fully Connected Neural networks (FCNs) on CIFAR-10, showing a short highly non-optimal regime followed by a longer optimal regime.