From Kernels to Features: A Multi-Scale Adaptive Theory of Feature Learning

Theoretically describing feature learning in neural networks is crucial for understanding their expressive power and inductive biases, motivating various approaches. Some approaches describe network behavior after training through a simple change in kernel scale from initialization, resulting in a generalization power comparable to a Gaussian process. Conversely, in other approaches training results in the adaptation of the kernel to the data, involving complex directional changes to the kernel. While these approaches capture different facets of network behavior, their relationship and respective strengths across scaling regimes remains an open question. This work presents a theoretical framework of multi-scale adaptive feature learning bridging these approaches. Using methods from statistical mechanics, we derive analytical expressions for network output statistics which are valid across scaling regimes and in the continuum between them. A systematic expansion of the network's probability distribution reveals that mean-field scaling requires only a saddle-point approximation, while standard scaling necessitates additional correction terms. Remarkably, we find across regimes that kernel adaptation can be reduced to an effective kernel rescaling when predicting the mean network output of a linear network. However, even in this case, the multi-scale adaptive approach captures directional feature learning effects, providing richer insights than what could be recovered from a rescaling of the kernel alone.

Identifying the impact of local connectivity patterns on dynamics in excitatory-inhibitory networks

Networks of excitatory and inhibitory (EI) neurons form a canonical circuit in the brain. Seminal theoretical results on dynamics of such networks are based on the assumption that synaptic strengths depend on the type of neurons they connect, but are otherwise statistically independent. Recent synaptic physiology datasets however highlight the prominence of specific connectivity patterns that go well beyond what is expected from independent connections. While decades of influential research have demonstrated the strong role of the basic EI cell type structure, to which extent additional connectivity features influence dynamics remains to be fully determined. Here we examine the effects of pairwise connectivity motifs on the linear dynamics in EI networks using an analytical framework that approximates the connectivity in terms of low-rank structures. This low-rank approximation is based on a mathematical derivation of the dominant eigenvalues of the connectivity matrix and predicts the impact on responses to external inputs of connectivity motifs and their interactions with cell-type structure. Our results reveal that a particular pattern of connectivity, chain motifs, have a much stronger impact on dominant eigenmodes than other pairwise motifs. An overrepresentation of chain motifs induces a strong positive eigenvalue in inhibition-dominated networks and generates a potential instability that requires revisiting the classical excitation-inhibition balance criteria. Examining effects of external inputs, we show that chain motifs can on their own induce paradoxical responses where an increased input to inhibitory neurons leads to a decrease in their activity due to the recurrent feedback. These findings have direct implications for the interpretation of experiments in which responses to optogenetic perturbations are measured and used to infer the dynamical regime of cortical circuits.

A theory of data variability in Neural Network Bayesian inference

Bayesian inference and kernel methods are well established in machine learning. The neural network Gaussian process in particular provides a concept to investigate neural networks in the limit of infinitely wide hidden layers by using kernel and inference methods. Here we build upon this limit and provide a field-theoretic formalism which covers the generalization properties of infinitely wide networks. We systematically compute generalization properties of linear, non-linear, and deep non-linear networks for kernel matrices with heterogeneous entries. In contrast to currently employed spectral methods we derive the generalization properties from the statistical properties of the input, elucidating the interplay of input dimensionality, size of the training data set, and variability of the data. We show that data variability leads to a non-Gaussian action reminiscent of a ($\varphi^3+\varphi^4$)-theory. Using our formalism on a synthetic task and on MNIST we obtain a homogeneous kernel matrix approximation for the learning curve as well as corrections due to data variability which allow the estimation of the generalization properties and exact results for the bounds of the learning curves in the case of infinitely many training data points.

Optimal signal propagation in ResNets through residual scaling

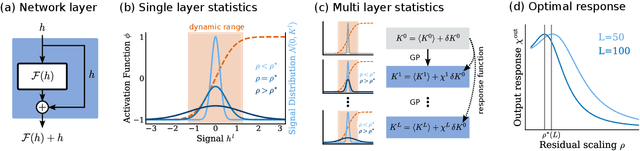
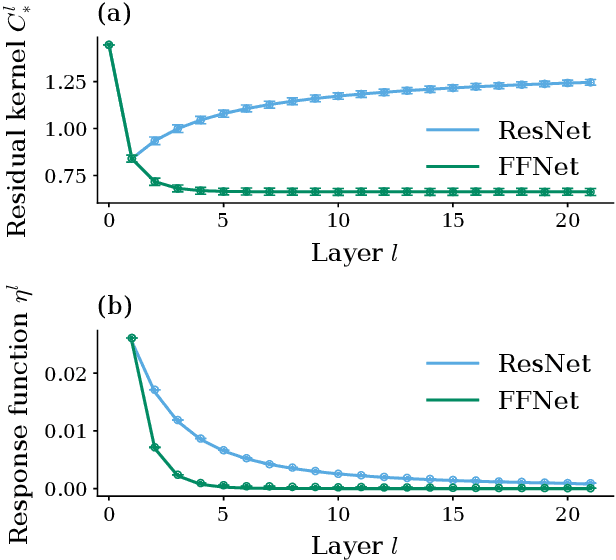
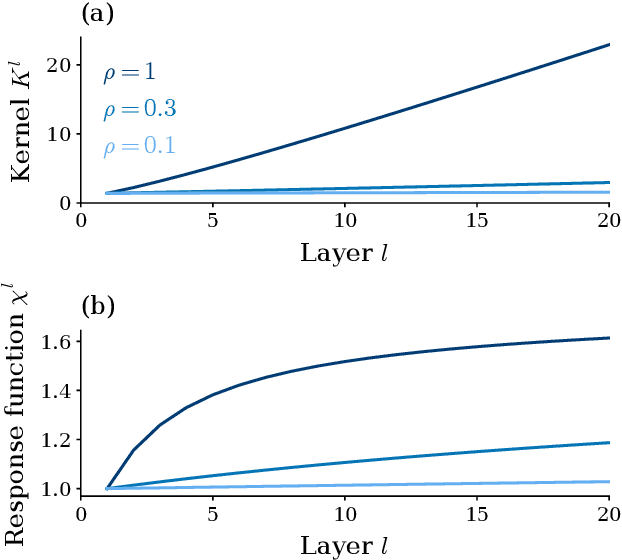
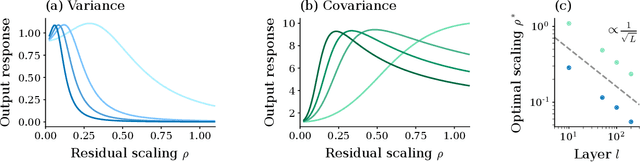
Residual networks (ResNets) have significantly better trainability and thus performance than feed-forward networks at large depth. Introducing skip connections facilitates signal propagation to deeper layers. In addition, previous works found that adding a scaling parameter for the residual branch further improves generalization performance. While they empirically identified a particularly beneficial range of values for this scaling parameter, the associated performance improvement and its universality across network hyperparameters yet need to be understood. For feed-forward networks (FFNets), finite-size theories have led to important insights with regard to signal propagation and hyperparameter tuning. We here derive a systematic finite-size theory for ResNets to study signal propagation and its dependence on the scaling for the residual branch. We derive analytical expressions for the response function, a measure for the network's sensitivity to inputs, and show that for deep networks the empirically found values for the scaling parameter lie within the range of maximal sensitivity. Furthermore, we obtain an analytical expression for the optimal scaling parameter that depends only weakly on other network hyperparameters, such as the weight variance, thereby explaining its universality across hyperparameters. Overall, this work provides a framework for theory-guided optimal scaling in ResNets and, more generally, provides the theoretical framework to study ResNets at finite widths.

Decomposing neural networks as mappings of correlation functions

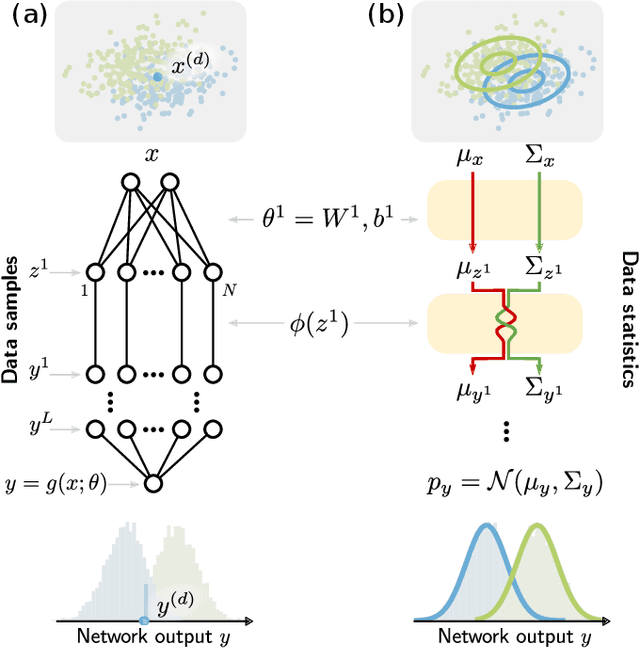
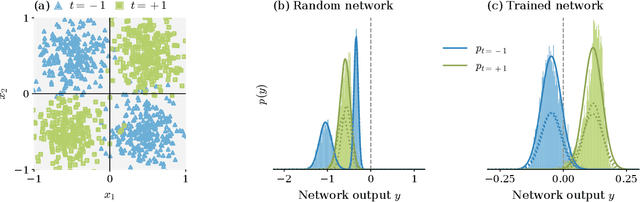
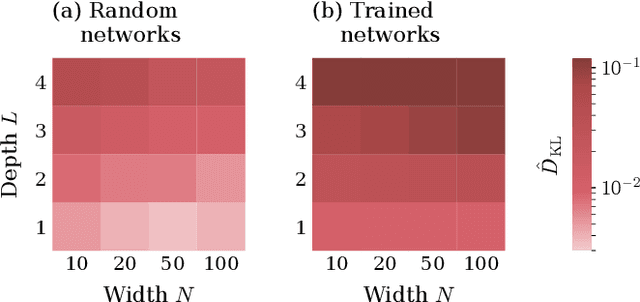
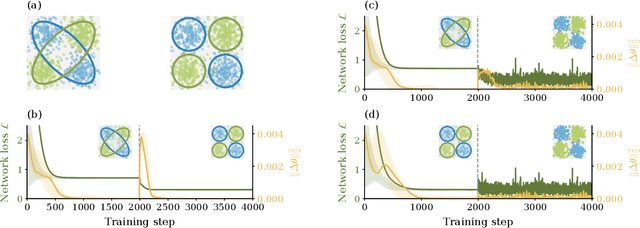
Understanding the functional principles of information processing in deep neural networks continues to be a challenge, in particular for networks with trained and thus non-random weights. To address this issue, we study the mapping between probability distributions implemented by a deep feed-forward network. We characterize this mapping as an iterated transformation of distributions, where the non-linearity in each layer transfers information between different orders of correlation functions. This allows us to identify essential statistics in the data, as well as different information representations that can be used by neural networks. Applied to an XOR task and to MNIST, we show that correlations up to second order predominantly capture the information processing in the internal layers, while the input layer also extracts higher-order correlations from the data. This analysis provides a quantitative and explainable perspective on classification.

Unified Field Theory for Deep and Recurrent Neural Networks

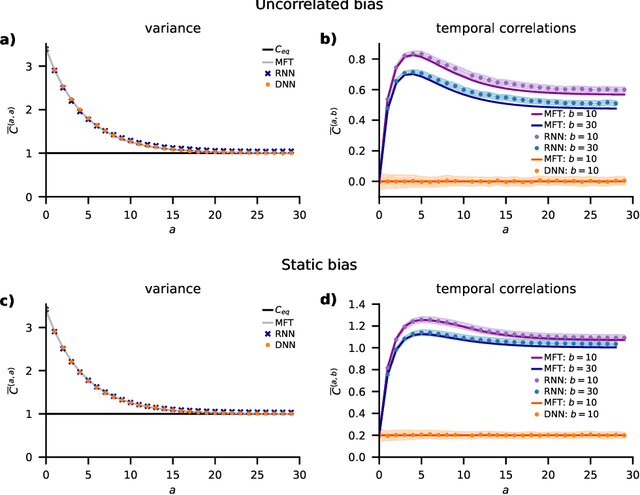
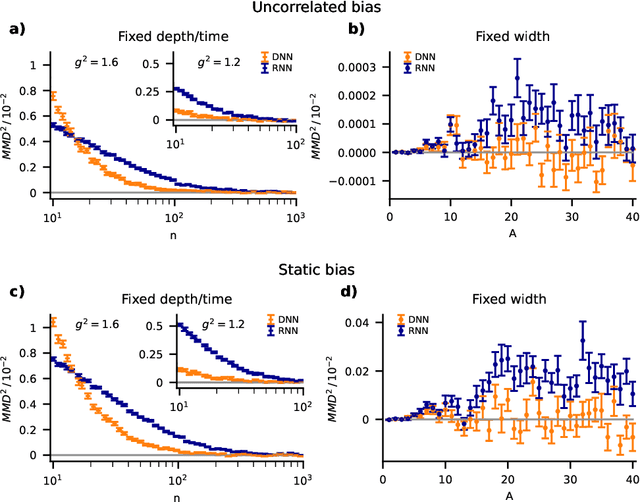
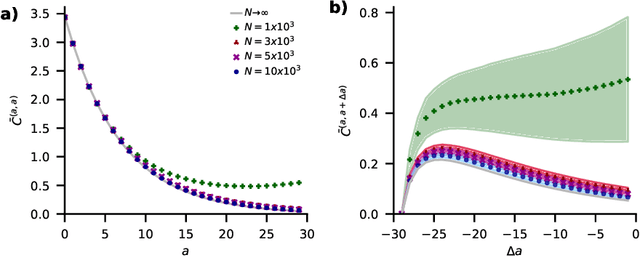
Understanding capabilities and limitations of different network architectures is of fundamental importance to machine learning. Bayesian inference on Gaussian processes has proven to be a viable approach for studying recurrent and deep networks in the limit of infinite layer width, $n\to\infty$. Here we present a unified and systematic derivation of the mean-field theory for both architectures that starts from first principles by employing established methods from statistical physics of disordered systems. The theory elucidates that while the mean-field equations are different with regard to their temporal structure, they yet yield identical Gaussian kernels when readouts are taken at a single time point or layer, respectively. Bayesian inference applied to classification then predicts identical performance and capabilities for the two architectures. Numerically, we find that convergence towards the mean-field theory is typically slower for recurrent networks than for deep networks and the convergence speed depends non-trivially on the parameters of the weight prior as well as the depth or number of time steps, respectively. Our method exposes that Gaussian processes are but the lowest order of a systematic expansion in $1/n$. The formalism thus paves the way to investigate the fundamental differences between recurrent and deep architectures at finite widths $n$.

Unfolding recurrence by Green's functions for optimized reservoir computing

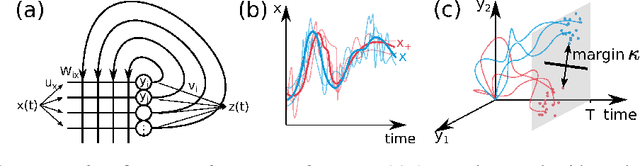
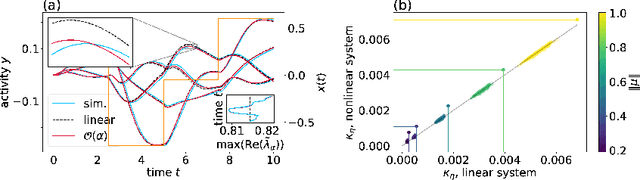
Cortical networks are strongly recurrent, and neurons have intrinsic temporal dynamics. This sets them apart from deep feed-forward networks. Despite the tremendous progress in the application of feed-forward networks and their theoretical understanding, it remains unclear how the interplay of recurrence and non-linearities in recurrent cortical networks contributes to their function. The purpose of this work is to present a solvable recurrent network model that links to feed forward networks. By perturbative methods we transform the time-continuous, recurrent dynamics into an effective feed-forward structure of linear and non-linear temporal kernels. The resulting analytical expressions allow us to build optimal time-series classifiers from random reservoir networks. Firstly, this allows us to optimize not only the readout vectors, but also the input projection, demonstrating a strong potential performance gain. Secondly, the analysis exposes how the second order stimulus statistics is a crucial element that interacts with the non-linearity of the dynamics and boosts performance.

Capacity of the covariance perceptron

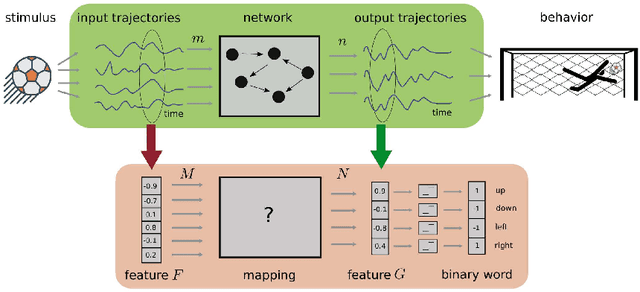
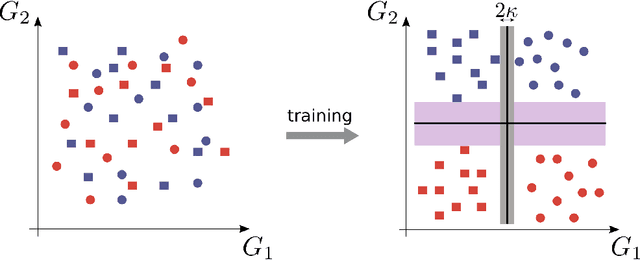
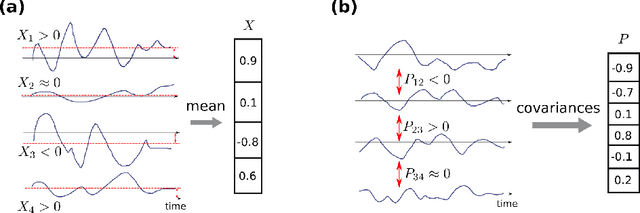
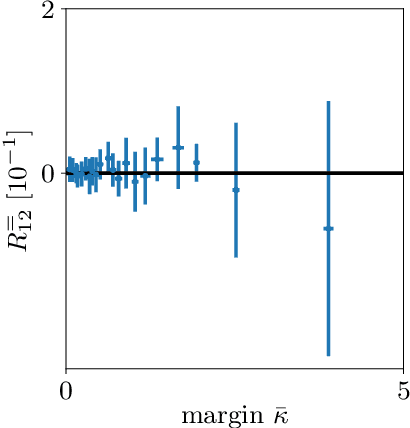
The classical perceptron is a simple neural network that performs a binary classification by a linear mapping between static inputs and outputs and application of a threshold. For small inputs, neural networks in a stationary state also perform an effectively linear input-output transformation, but of an entire time series. Choosing the temporal mean of the time series as the feature for classification, the linear transformation of the network with subsequent thresholding is equivalent to the classical perceptron. Here we show that choosing covariances of time series as the feature for classification maps the neural network to what we call a 'covariance perceptron'; a bilinear mapping between covariances. By extending Gardner's theory of connections to this bilinear problem, using a replica symmetric mean-field theory, we compute the pattern and information capacities of the covariance perceptron in the infinite-size limit. Closed-form expressions reveal superior pattern capacity in the binary classification task compared to the classical perceptron in the case of a high-dimensional input and low-dimensional output. For less convergent networks, the mean perceptron classifies a larger number of stimuli. However, since covariances span a much larger input and output space than means, the amount of stored information in the covariance perceptron exceeds the classical counterpart. For strongly convergent connectivity it is superior by a factor equal to the number of input neurons. Theoretical calculations are validated numerically for finite size systems using a gradient-based optimization of a soft-margin, as well as numerical solvers for the NP hard quadratically constrained quadratic programming problem, to which training can be mapped.