Optimal thresholds and algorithms for a model of multi-modal learning in high dimensions

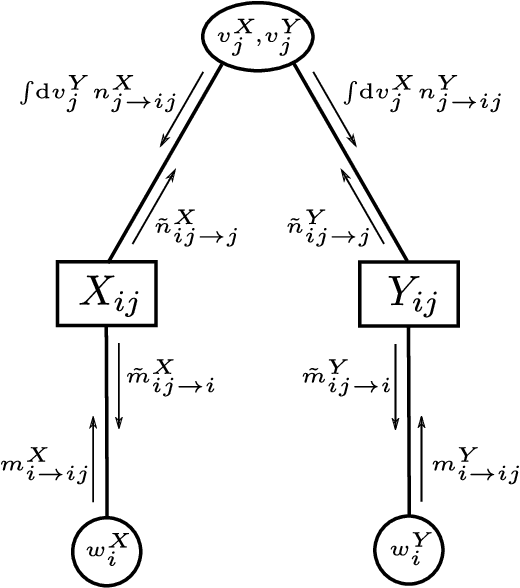
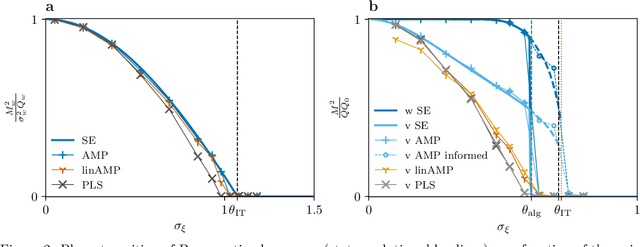
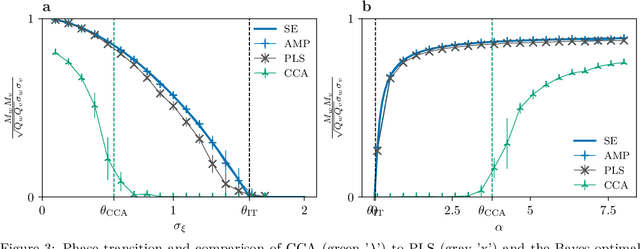
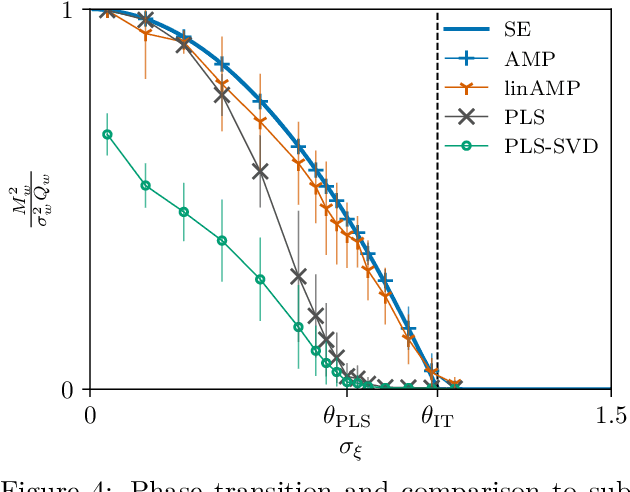
This work explores multi-modal inference in a high-dimensional simplified model, analytically quantifying the performance gain of multi-modal inference over that of analyzing modalities in isolation. We present the Bayes-optimal performance and weak recovery thresholds in a model where the objective is to recover the latent structures from two noisy data matrices with correlated spikes. The paper derives the approximate message passing (AMP) algorithm for this model and characterizes its performance in the high-dimensional limit via the associated state evolution. The analysis holds for a broad range of priors and noise channels, which can differ across modalities. The linearization of AMP is compared numerically to the widely used partial least squares (PLS) and canonical correlation analysis (CCA) methods, which are both observed to suffer from a sub-optimal recovery threshold.

Les Houches Lectures on Deep Learning at Large & Infinite Width

These lectures, presented at the 2022 Les Houches Summer School on Statistical Physics and Machine Learning, focus on the infinite-width limit and large-width regime of deep neural networks. Topics covered include various statistical and dynamical properties of these networks. In particular, the lecturers discuss properties of random deep neural networks; connections between trained deep neural networks, linear models, kernels, and Gaussian processes that arise in the infinite-width limit; and perturbative and non-perturbative treatments of large but finite-width networks, at initialization and after training.

Origami in N dimensions: How feed-forward networks manufacture linear separability

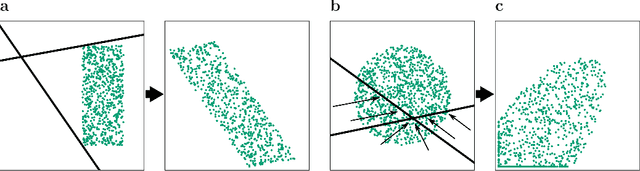
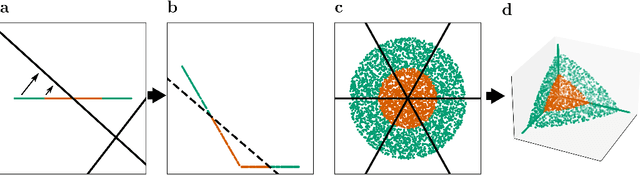
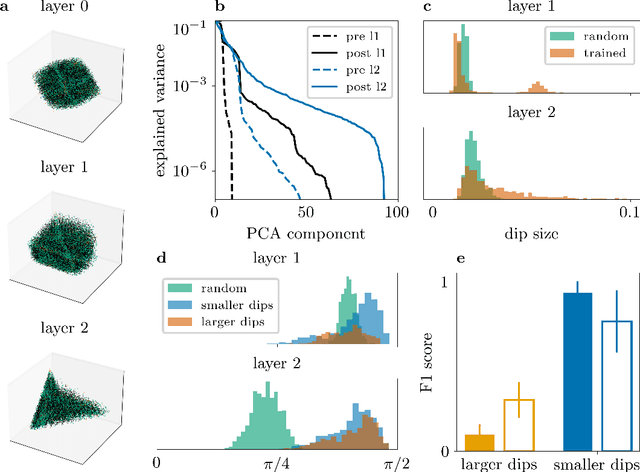
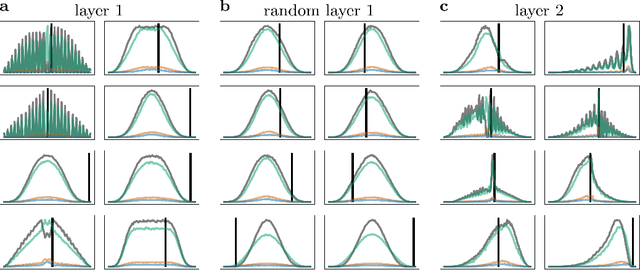
Neural networks can implement arbitrary functions. But, mechanistically, what are the tools at their disposal to construct the target? For classification tasks, the network must transform the data classes into a linearly separable representation in the final hidden layer. We show that a feed-forward architecture has one primary tool at hand to achieve this separability: progressive folding of the data manifold in unoccupied higher dimensions. The operation of folding provides a useful intuition in low-dimensions that generalizes to high ones. We argue that an alternative method based on shear, requiring very deep architectures, plays only a small role in real-world networks. The folding operation, however, is powerful as long as layers are wider than the data dimensionality, allowing efficient solutions by providing access to arbitrary regions in the distribution, such as data points of one class forming islands within the other classes. We argue that a link exists between the universal approximation property in ReLU networks and the fold-and-cut theorem (Demaine et al., 1998) dealing with physical paper folding. Based on the mechanistic insight, we predict that the progressive generation of separability is necessarily accompanied by neurons showing mixed selectivity and bimodal tuning curves. This is validated in a network trained on the poker hand task, showing the emergence of bimodal tuning curves during training. We hope that our intuitive picture of the data transformation in deep networks can help to provide interpretability, and discuss possible applications to the theory of convolutional networks, loss landscapes, and generalization. TL;DR: Shows that the internal processing of deep networks can be thought of as literal folding operations on the data distribution in the N-dimensional activation space. A link to a well-known theorem in origami theory is provided.

Decomposing neural networks as mappings of correlation functions

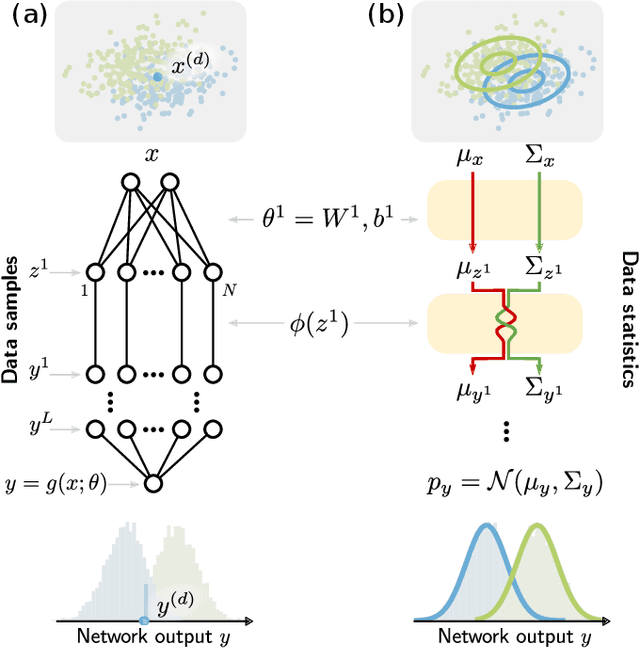
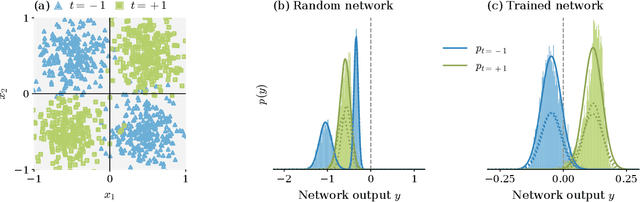
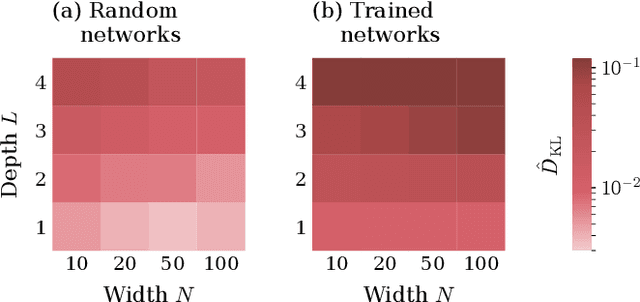
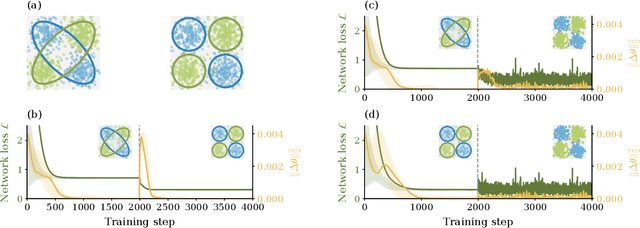
Understanding the functional principles of information processing in deep neural networks continues to be a challenge, in particular for networks with trained and thus non-random weights. To address this issue, we study the mapping between probability distributions implemented by a deep feed-forward network. We characterize this mapping as an iterated transformation of distributions, where the non-linearity in each layer transfers information between different orders of correlation functions. This allows us to identify essential statistics in the data, as well as different information representations that can be used by neural networks. Applied to an XOR task and to MNIST, we show that correlations up to second order predominantly capture the information processing in the internal layers, while the input layer also extracts higher-order correlations from the data. This analysis provides a quantitative and explainable perspective on classification.

Unfolding recurrence by Green's functions for optimized reservoir computing

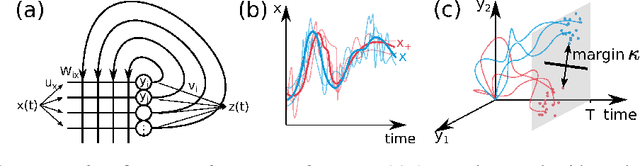
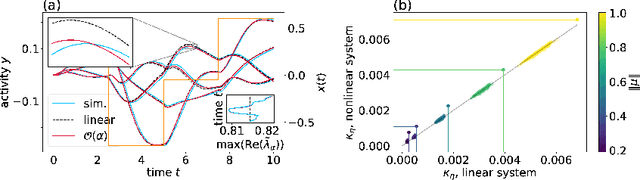
Cortical networks are strongly recurrent, and neurons have intrinsic temporal dynamics. This sets them apart from deep feed-forward networks. Despite the tremendous progress in the application of feed-forward networks and their theoretical understanding, it remains unclear how the interplay of recurrence and non-linearities in recurrent cortical networks contributes to their function. The purpose of this work is to present a solvable recurrent network model that links to feed forward networks. By perturbative methods we transform the time-continuous, recurrent dynamics into an effective feed-forward structure of linear and non-linear temporal kernels. The resulting analytical expressions allow us to build optimal time-series classifiers from random reservoir networks. Firstly, this allows us to optimize not only the readout vectors, but also the input projection, demonstrating a strong potential performance gain. Secondly, the analysis exposes how the second order stimulus statistics is a crucial element that interacts with the non-linearity of the dynamics and boosts performance.