Alternating Gradient Flows: A Theory of Feature Learning in Two-layer Neural Networks

What features neural networks learn, and how, remains an open question. In this paper, we introduce Alternating Gradient Flows (AGF), an algorithmic framework that describes the dynamics of feature learning in two-layer networks trained from small initialization. Prior works have shown that gradient flow in this regime exhibits a staircase-like loss curve, alternating between plateaus where neurons slowly align to useful directions and sharp drops where neurons rapidly grow in norm. AGF approximates this behavior as an alternating two-step process: maximizing a utility function over dormant neurons and minimizing a cost function over active ones. AGF begins with all neurons dormant. At each round, a dormant neuron activates, triggering the acquisition of a feature and a drop in the loss. AGF quantifies the order, timing, and magnitude of these drops, matching experiments across architectures. We show that AGF unifies and extends existing saddle-to-saddle analyses in fully connected linear networks and attention-only linear transformers, where the learned features are singular modes and principal components, respectively. In diagonal linear networks, we prove AGF converges to gradient flow in the limit of vanishing initialization. Applying AGF to quadratic networks trained to perform modular addition, we give the first complete characterization of the training dynamics, revealing that networks learn Fourier features in decreasing order of coefficient magnitude. Altogether, AGF offers a promising step towards understanding feature learning in neural networks.

Saddle-To-Saddle Dynamics in Deep ReLU Networks: Low-Rank Bias in the First Saddle Escape

When a deep ReLU network is initialized with small weights, GD is at first dominated by the saddle at the origin in parameter space. We study the so-called escape directions, which play a similar role as the eigenvectors of the Hessian for strict saddles. We show that the optimal escape direction features a low-rank bias in its deeper layers: the first singular value of the $\ell$-th layer weight matrix is at least $\ell^{\frac{1}{4}}$ larger than any other singular value. We also prove a number of related results about these escape directions. We argue that this result is a first step in proving Saddle-to-Saddle dynamics in deep ReLU networks, where GD visits a sequence of saddles with increasing bottleneck rank.

The Optimization Landscape of SGD Across the Feature Learning Strength

We consider neural networks (NNs) where the final layer is down-scaled by a fixed hyperparameter $\gamma$. Recent work has identified $\gamma$ as controlling the strength of feature learning. As $\gamma$ increases, network evolution changes from ``lazy'' kernel dynamics to ``rich'' feature-learning dynamics, with a host of associated benefits including improved performance on common tasks. In this work, we conduct a thorough empirical investigation of the effect of scaling $\gamma$ across a variety of models and datasets in the online training setting. We first examine the interaction of $\gamma$ with the learning rate $\eta$, identifying several scaling regimes in the $\gamma$-$\eta$ plane which we explain theoretically using a simple model. We find that the optimal learning rate $\eta^*$ scales non-trivially with $\gamma$. In particular, $\eta^* \propto \gamma^2$ when $\gamma \ll 1$ and $\eta^* \propto \gamma^{2/L}$ when $\gamma \gg 1$ for a feed-forward network of depth $L$. Using this optimal learning rate scaling, we proceed with an empirical study of the under-explored ``ultra-rich'' $\gamma \gg 1$ regime. We find that networks in this regime display characteristic loss curves, starting with a long plateau followed by a drop-off, sometimes followed by one or more additional staircase steps. We find networks of different large $\gamma$ values optimize along similar trajectories up to a reparameterization of time. We further find that optimal online performance is often found at large $\gamma$ and could be missed if this hyperparameter is not tuned. Our findings indicate that analytical study of the large-$\gamma$ limit may yield useful insights into the dynamics of representation learning in performant models.

More is Better in Modern Machine Learning: when Infinite Overparameterization is Optimal and Overfitting is Obligatory

In our era of enormous neural networks, empirical progress has been driven by the philosophy that more is better. Recent deep learning practice has found repeatedly that larger model size, more data, and more computation (resulting in lower training loss) improves performance. In this paper, we give theoretical backing to these empirical observations by showing that these three properties hold in random feature (RF) regression, a class of models equivalent to shallow networks with only the last layer trained. Concretely, we first show that the test risk of RF regression decreases monotonically with both the number of features and the number of samples, provided the ridge penalty is tuned optimally. In particular, this implies that infinite width RF architectures are preferable to those of any finite width. We then proceed to demonstrate that, for a large class of tasks characterized by powerlaw eigenstructure, training to near-zero training loss is obligatory: near-optimal performance can only be achieved when the training error is much smaller than the test error. Grounding our theory in real-world data, we find empirically that standard computer vision tasks with convolutional neural tangent kernels clearly fall into this class. Taken together, our results tell a simple, testable story of the benefits of overparameterization, overfitting, and more data in random feature models.

A Spectral Condition for Feature Learning

The push to train ever larger neural networks has motivated the study of initialization and training at large network width. A key challenge is to scale training so that a network's internal representations evolve nontrivially at all widths, a process known as feature learning. Here, we show that feature learning is achieved by scaling the spectral norm of weight matrices and their updates like $\sqrt{\texttt{fan-out}/\texttt{fan-in}}$, in contrast to widely used but heuristic scalings based on Frobenius norm and entry size. Our spectral scaling analysis also leads to an elementary derivation of \emph{maximal update parametrization}. All in all, we aim to provide the reader with a solid conceptual understanding of feature learning in neural networks.

Les Houches Lectures on Deep Learning at Large & Infinite Width

These lectures, presented at the 2022 Les Houches Summer School on Statistical Physics and Machine Learning, focus on the infinite-width limit and large-width regime of deep neural networks. Topics covered include various statistical and dynamical properties of these networks. In particular, the lecturers discuss properties of random deep neural networks; connections between trained deep neural networks, linear models, kernels, and Gaussian processes that arise in the infinite-width limit; and perturbative and non-perturbative treatments of large but finite-width networks, at initialization and after training.

An Agnostic View on the Cost of Overfitting in Ridge Regression

We study the cost of overfitting in noisy kernel ridge regression (KRR), which we define as the ratio between the test error of the interpolating ridgeless model and the test error of the optimally-tuned model. We take an "agnostic" view in the following sense: we consider the cost as a function of sample size for any target function, even if the sample size is not large enough for consistency or the target is outside the RKHS. We analyze the cost of overfitting under a Gaussian universality ansatz using recently derived (non-rigorous) risk estimates in terms of the task eigenstructure. Our analysis provides a more refined characterization of benign, tempered and catastrophic overfitting (qv Mallinar et al. 2022).

Tune As You Scale: Hyperparameter Optimization For Compute Efficient Training

Hyperparameter tuning of deep learning models can lead to order-of-magnitude performance gains for the same amount of compute. Despite this, systematic tuning is uncommon, particularly for large models, which are expensive to evaluate and tend to have many hyperparameters, necessitating difficult judgment calls about tradeoffs, budgets, and search bounds. To address these issues and propose a practical method for robustly tuning large models, we present Cost-Aware Pareto Region Bayesian Search (CARBS), a Bayesian optimization algorithm that performs local search around the performance-cost Pareto frontier. CARBS does well even in unbounded search spaces with many hyperparameters, learns scaling relationships so that it can tune models even as they are scaled up, and automates much of the "black magic" of tuning. Among our results, we effectively solve the entire ProcGen benchmark just by tuning a simple baseline (PPO, as provided in the original ProcGen paper). We also reproduce the model size vs. training tokens scaling result from the Chinchilla project (Hoffmann et al. 2022), while simultaneously discovering scaling laws for every other hyperparameter, via an easy automated process that uses significantly less compute and is applicable to any deep learning problem (not just language models).

On the stepwise nature of self-supervised learning

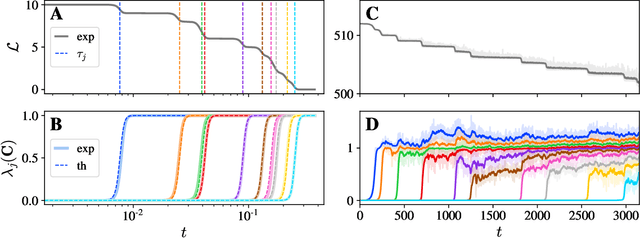
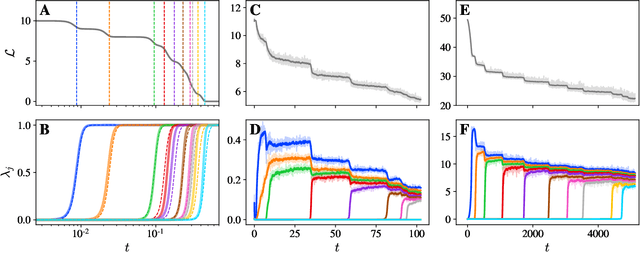
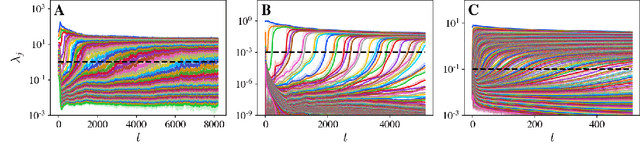
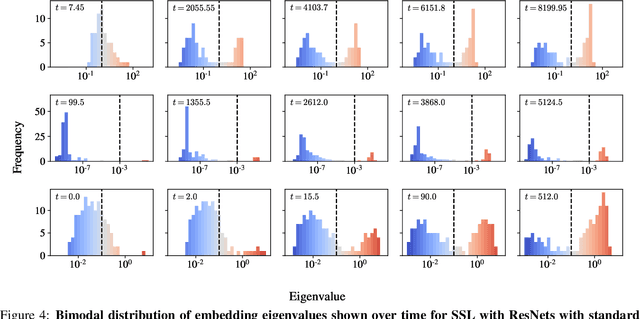
We present a simple picture of the training process of self-supervised learning methods with joint embedding networks. We find that these methods learn their high-dimensional embeddings one dimension at a time in a sequence of discrete, well-separated steps. We arrive at this conclusion via the study of a linearized model of Barlow Twins applicable to the case in which the trained network is infinitely wide. We solve the training dynamics of this model from small initialization, finding that the model learns the top eigenmodes of a certain contrastive kernel in a stepwise fashion, and obtain a closed-form expression for the final learned representations. Remarkably, we then see the same stepwise learning phenomenon when training deep ResNets using the Barlow Twins, SimCLR, and VICReg losses. Our theory suggests that, just as kernel regression can be thought of as a model of supervised learning, \textit{kernel PCA} may serve as a useful model of self-supervised learning.

Avalon: A Benchmark for RL Generalization Using Procedurally Generated Worlds

Despite impressive successes, deep reinforcement learning (RL) systems still fall short of human performance on generalization to new tasks and environments that differ from their training. As a benchmark tailored for studying RL generalization, we introduce Avalon, a set of tasks in which embodied agents in highly diverse procedural 3D worlds must survive by navigating terrain, hunting or gathering food, and avoiding hazards. Avalon is unique among existing RL benchmarks in that the reward function, world dynamics, and action space are the same for every task, with tasks differentiated solely by altering the environment; its 20 tasks, ranging in complexity from eat and throw to hunt and navigate, each create worlds in which the agent must perform specific skills in order to survive. This setup enables investigations of generalization within tasks, between tasks, and to compositional tasks that require combining skills learned from previous tasks. Avalon includes a highly efficient simulator, a library of baselines, and a benchmark with scoring metrics evaluated against hundreds of hours of human performance, all of which are open-source and publicly available. We find that standard RL baselines make progress on most tasks but are still far from human performance, suggesting Avalon is challenging enough to advance the quest for generalizable RL.