Neural Tangent Kernel Eigenvalues Accurately Predict Generalization

Finding a quantitative theory of neural network generalization has long been a central goal of deep learning research. We extend recent results to demonstrate that, by examining the eigensystem of a neural network's "neural tangent kernel", one can predict its generalization performance when learning arbitrary functions. Our theory accurately predicts not only test mean-squared-error but all first- and second-order statistics of the network's learned function. Furthermore, using a measure quantifying the "learnability" of a given target function, we prove a new "no-free-lunch" theorem characterizing a fundamental tradeoff in the inductive bias of wide neural networks: improving a network's generalization for a given target function must worsen its generalization for orthogonal functions. We further demonstrate the utility of our theory by analytically predicting two surprising phenomena - worse-than-chance generalization on hard-to-learn functions and nonmonotonic error curves in the small data regime - which we subsequently observe in experiments. Though our theory is derived for infinite-width architectures, we find it agrees with networks as narrow as width 20, suggesting it is predictive of generalization in practical neural networks. Code replicating our results is available at https://github.com/james-simon/eigenlearning.

On the Power of Shallow Learning

A deluge of recent work has explored equivalences between wide neural networks and kernel methods. A central theme is that one can analytically find the kernel corresponding to a given wide network architecture, but despite major implications for architecture design, no work to date has asked the converse question: given a kernel, can one find a network that realizes it? We affirmatively answer this question for fully-connected architectures, completely characterizing the space of achievable kernels. Furthermore, we give a surprising constructive proof that any kernel of any wide, deep, fully-connected net can also be achieved with a network with just one hidden layer and a specially-designed pointwise activation function. We experimentally verify our construction and demonstrate that, by just choosing the activation function, we can design a wide shallow network that mimics the generalization performance of any wide, deep, fully-connected network.

A new method for parameter estimation in probabilistic models: Minimum probability flow

Fitting probabilistic models to data is often difficult, due to the general intractability of the partition function. We propose a new parameter fitting method, Minimum Probability Flow (MPF), which is applicable to any parametric model. We demonstrate parameter estimation using MPF in two cases: a continuous state space model, and an Ising spin glass. In the latter case it outperforms current techniques by at least an order of magnitude in convergence time with lower error in the recovered coupling parameters.

Critical Point-Finding Methods Reveal Gradient-Flat Regions of Deep Network Losses

Despite the fact that the loss functions of deep neural networks are highly non-convex, gradient-based optimization algorithms converge to approximately the same performance from many random initial points. One thread of work has focused on explaining this phenomenon by characterizing the local curvature near critical points of the loss function, where the gradients are near zero, and demonstrating that neural network losses enjoy a no-bad-local-minima property and an abundance of saddle points. We report here that the methods used to find these putative critical points suffer from a bad local minima problem of their own: they often converge to or pass through regions where the gradient norm has a stationary point. We call these gradient-flat regions, since they arise when the gradient is approximately in the kernel of the Hessian, such that the loss is locally approximately linear, or flat, in the direction of the gradient. We describe how the presence of these regions necessitates care in both interpreting past results that claimed to find critical points of neural network losses and in designing second-order methods for optimizing neural networks.

Design of optical neural networks with component imprecisions

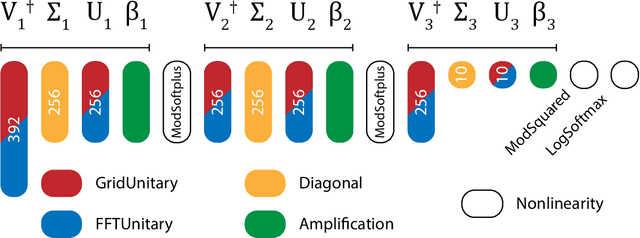
For the benefit of designing scalable, fault resistant optical neural networks (ONNs), we investigate the effects architectural designs have on the ONNs' robustness to imprecise components. We train two ONNs -- one with a more tunable design (GridNet) and one with better fault tolerance (FFTNet) -- to classify handwritten digits. When simulated without any imperfections, GridNet yields a better accuracy (~98%) than FFTNet (~95%). However, under a small amount of error in their photonic components, the more fault tolerant FFTNet overtakes GridNet. We further provide thorough quantitative and qualitative analyses of ONNs' sensitivity to varying levels and types of imprecisions. Our results offer guidelines for the principled design of fault-tolerant ONNs as well as a foundation for further research.

Numerically Recovering the Critical Points of a Deep Linear Autoencoder

Numerically locating the critical points of non-convex surfaces is a long-standing problem central to many fields. Recently, the loss surfaces of deep neural networks have been explored to gain insight into outstanding questions in optimization, generalization, and network architecture design. However, the degree to which recently-proposed methods for numerically recovering critical points actually do so has not been thoroughly evaluated. In this paper, we examine this issue in a case for which the ground truth is known: the deep linear autoencoder. We investigate two sub-problems associated with numerical critical point identification: first, because of large parameter counts, it is infeasible to find all of the critical points for contemporary neural networks, necessitating sampling approaches whose characteristics are poorly understood; second, the numerical tolerance for accurately identifying a critical point is unknown, and conservative tolerances are difficult to satisfy. We first identify connections between recently-proposed methods and well-understood methods in other fields, including chemical physics, economics, and algebraic geometry. We find that several methods work well at recovering certain information about loss surfaces, but fail to take an unbiased sample of critical points. Furthermore, numerical tolerance must be very strict to ensure that numerically-identified critical points have similar properties to true analytical critical points. We also identify a recently-published Newton method for optimization that outperforms previous methods as a critical point-finding algorithm. We expect our results will guide future attempts to numerically study critical points in large nonlinear neural networks.

Hamiltonian Monte Carlo Without Detailed Balance

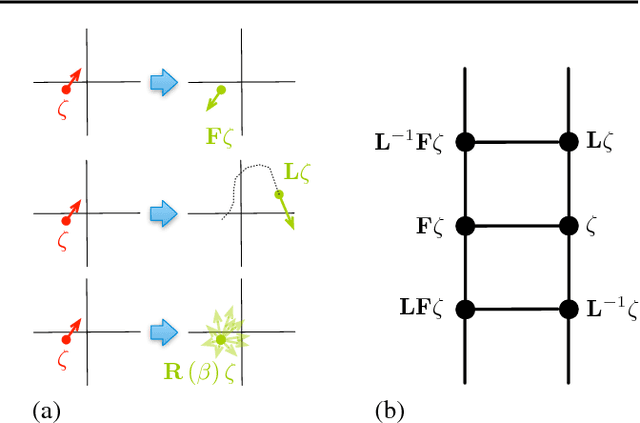
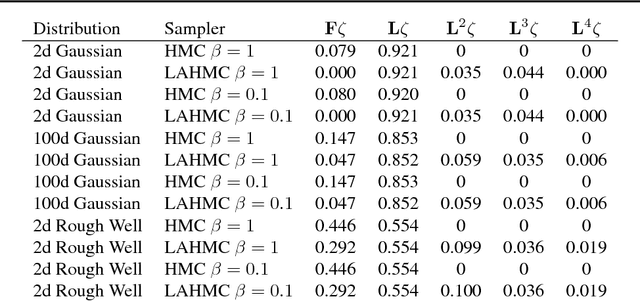
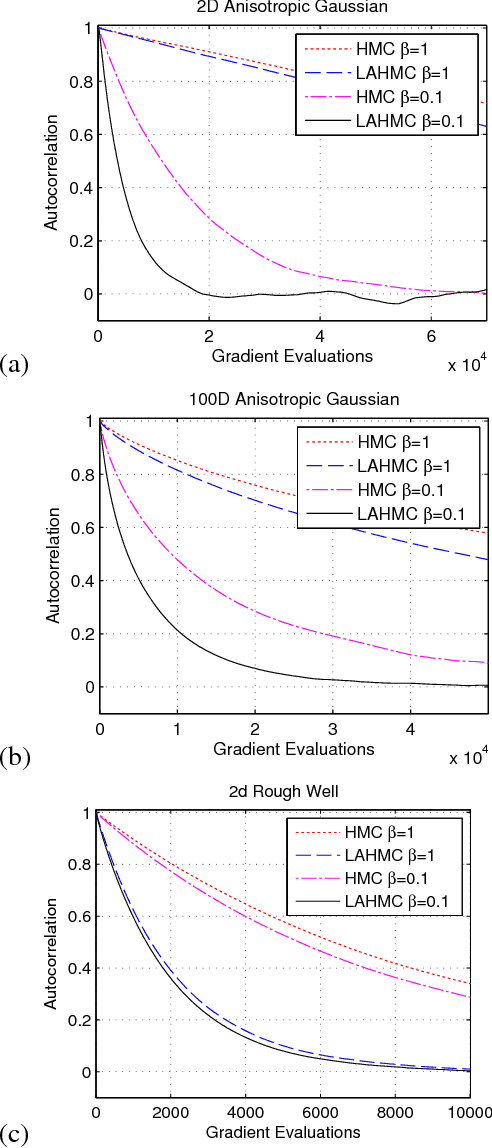
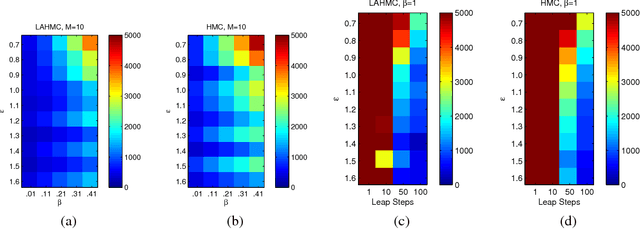
We present a method for performing Hamiltonian Monte Carlo that largely eliminates sample rejection for typical hyperparameters. In situations that would normally lead to rejection, instead a longer trajectory is computed until a new state is reached that can be accepted. This is achieved using Markov chain transitions that satisfy the fixed point equation, but do not satisfy detailed balance. The resulting algorithm significantly suppresses the random walk behavior and wasted function evaluations that are typically the consequence of update rejection. We demonstrate a greater than factor of two improvement in mixing time on three test problems. We release the source code as Python and MATLAB packages.

A Markov Jump Process for More Efficient Hamiltonian Monte Carlo

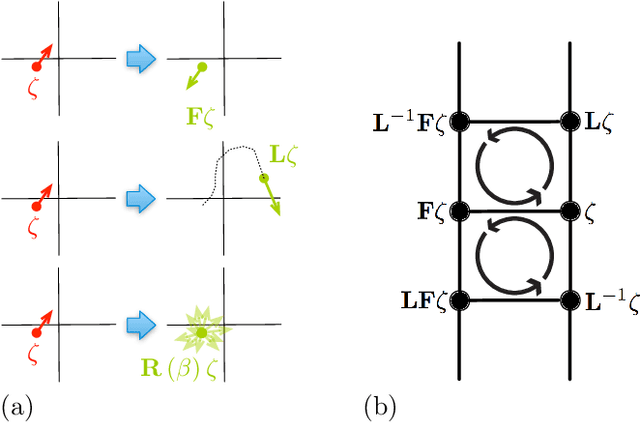
In most sampling algorithms, including Hamiltonian Monte Carlo, transition rates between states correspond to the probability of making a transition in a single time step, and are constrained to be less than or equal to 1. We derive a Hamiltonian Monte Carlo algorithm using a continuous time Markov jump process, and are thus able to escape this constraint. Transition rates in a Markov jump process need only be non-negative. We demonstrate that the new algorithm leads to improved mixing for several example problems, both by evaluating the spectral gap of the Markov operator, and by computing autocorrelation as a function of compute time. We release the algorithm as an open source Python package.

Time Resolution Dependence of Information Measures for Spiking Neurons: Atoms, Scaling, and Universality

The mutual information between stimulus and spike-train response is commonly used to monitor neural coding efficiency, but neuronal computation broadly conceived requires more refined and targeted information measures of input-output joint processes. A first step towards that larger goal is to develop information measures for individual output processes, including information generation (entropy rate), stored information (statistical complexity), predictable information (excess entropy), and active information accumulation (bound information rate). We calculate these for spike trains generated by a variety of noise-driven integrate-and-fire neurons as a function of time resolution and for alternating renewal processes. We show that their time-resolution dependence reveals coarse-grained structural properties of interspike interval statistics; e.g., $\tau$-entropy rates that diverge less quickly than the firing rate indicate interspike interval correlations. We also find evidence that the excess entropy and regularized statistical complexity of different types of integrate-and-fire neurons are universal in the continuous-time limit in the sense that they do not depend on mechanism details. This suggests a surprising simplicity in the spike trains generated by these model neurons. Interestingly, neurons with gamma-distributed ISIs and neurons whose spike trains are alternating renewal processes do not fall into the same universality class. These results lead to two conclusions. First, the dependence of information measures on time resolution reveals mechanistic details about spike train generation. Second, information measures can be used as model selection tools for analyzing spike train processes.

Minimum Probability Flow Learning

Fitting probabilistic models to data is often difficult, due to the general intractability of the partition function and its derivatives. Here we propose a new parameter estimation technique that does not require computing an intractable normalization factor or sampling from the equilibrium distribution of the model. This is achieved by establishing dynamics that would transform the observed data distribution into the model distribution, and then setting as the objective the minimization of the KL divergence between the data distribution and the distribution produced by running the dynamics for an infinitesimal time. Score matching, minimum velocity learning, and certain forms of contrastive divergence are shown to be special cases of this learning technique. We demonstrate parameter estimation in Ising models, deep belief networks and an independent component analysis model of natural scenes. In the Ising model case, current state of the art techniques are outperformed by at least an order of magnitude in learning time, with lower error in recovered coupling parameters.