Efficient Optimization with Higher-Order Ising Machines

A prominent approach to solving combinatorial optimization problems on parallel hardware is Ising machines, i.e., hardware implementations of networks of interacting binary spin variables. Most Ising machines leverage second-order interactions although important classes of optimization problems, such as satisfiability problems, map more seamlessly to Ising networks with higher-order interactions. Here, we demonstrate that higher-order Ising machines can solve satisfiability problems more resource-efficiently in terms of the number of spin variables and their connections when compared to traditional second-order Ising machines. Further, our results show on a benchmark dataset of Boolean \textit{k}-satisfiability problems that higher-order Ising machines implemented with coupled oscillators rapidly find solutions that are better than second-order Ising machines, thus, improving the current state-of-the-art for Ising machines.

Learning and Inference in Sparse Coding Models with Langevin Dynamics

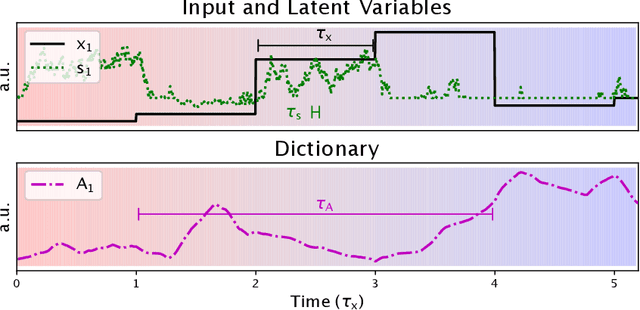
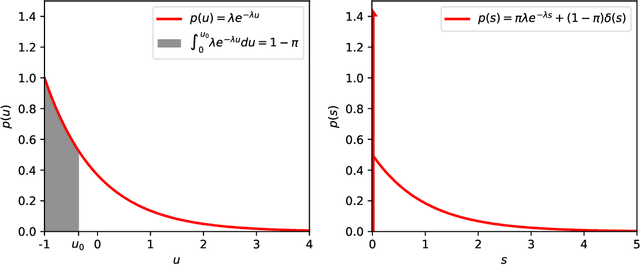
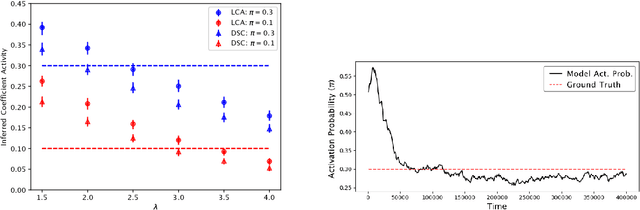
We describe a stochastic, dynamical system capable of inference and learning in a probabilistic latent variable model. The most challenging problem in such models - sampling the posterior distribution over latent variables - is proposed to be solved by harnessing natural sources of stochasticity inherent in electronic and neural systems. We demonstrate this idea for a sparse coding model by deriving a continuous-time equation for inferring its latent variables via Langevin dynamics. The model parameters are learned by simultaneously evolving according to another continuous-time equation, thus bypassing the need for digital accumulators or a global clock. Moreover we show that Langevin dynamics lead to an efficient procedure for sampling from the posterior distribution in the 'L0 sparse' regime, where latent variables are encouraged to be set to zero as opposed to having a small L1 norm. This allows the model to properly incorporate the notion of sparsity rather than having to resort to a relaxed version of sparsity to make optimization tractable. Simulations of the proposed dynamical system on both synthetic and natural image datasets demonstrate that the model is capable of probabilistically correct inference, enabling learning of the dictionary as well as parameters of the prior.

Integer Factorization with Compositional Distributed Representations

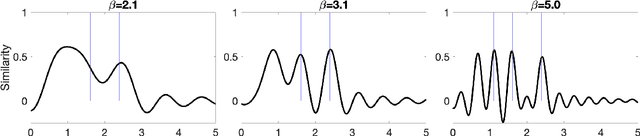
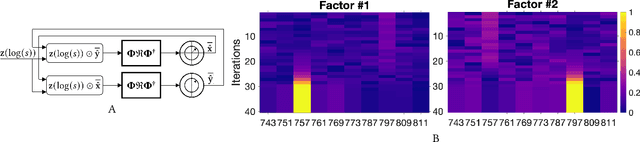
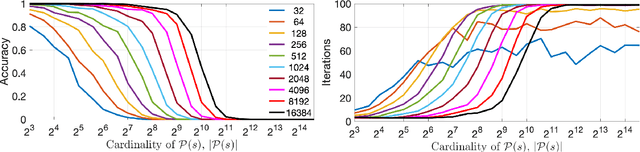
In this paper, we present an approach to integer factorization using distributed representations formed with Vector Symbolic Architectures. The approach formulates integer factorization in a manner such that it can be solved using neural networks and potentially implemented on parallel neuromorphic hardware. We introduce a method for encoding numbers in distributed vector spaces and explain how the resonator network can solve the integer factorization problem. We evaluate the approach on factorization of semiprimes by measuring the factorization accuracy versus the scale of the problem. We also demonstrate how the proposed approach generalizes beyond the factorization of semiprimes; in principle, it can be used for factorization of any composite number. This work demonstrates how a well-known combinatorial search problem may be formulated and solved within the framework of Vector Symbolic Architectures, and it opens the door to solving similarly difficult problems in other domains.

Design of optical neural networks with component imprecisions

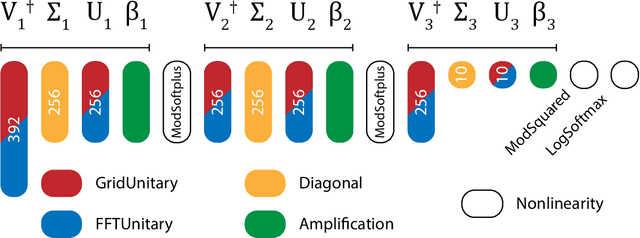
For the benefit of designing scalable, fault resistant optical neural networks (ONNs), we investigate the effects architectural designs have on the ONNs' robustness to imprecise components. We train two ONNs -- one with a more tunable design (GridNet) and one with better fault tolerance (FFTNet) -- to classify handwritten digits. When simulated without any imperfections, GridNet yields a better accuracy (~98%) than FFTNet (~95%). However, under a small amount of error in their photonic components, the more fault tolerant FFTNet overtakes GridNet. We further provide thorough quantitative and qualitative analyses of ONNs' sensitivity to varying levels and types of imprecisions. Our results offer guidelines for the principled design of fault-tolerant ONNs as well as a foundation for further research.

Flexpoint: An Adaptive Numerical Format for Efficient Training of Deep Neural Networks

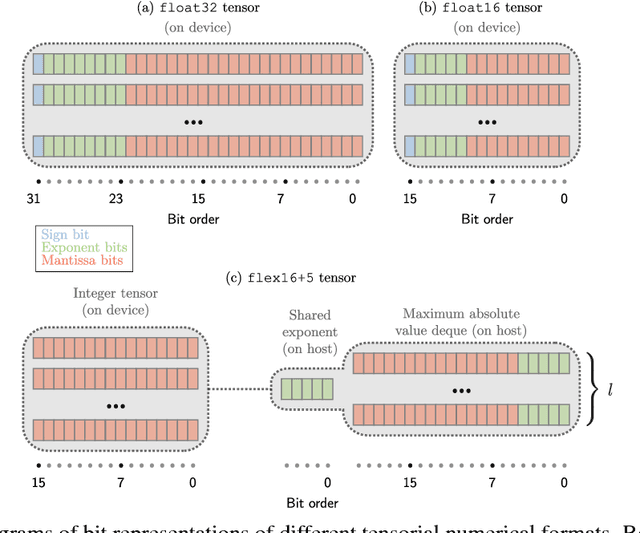
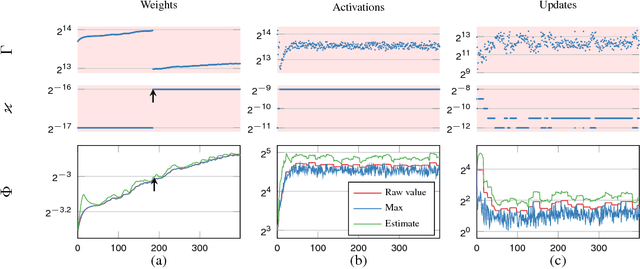
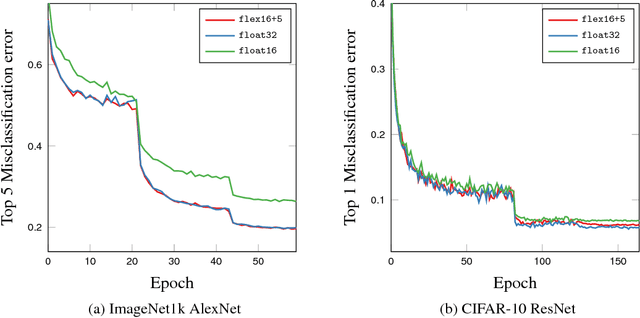
Deep neural networks are commonly developed and trained in 32-bit floating point format. Significant gains in performance and energy efficiency could be realized by training and inference in numerical formats optimized for deep learning. Despite advances in limited precision inference in recent years, training of neural networks in low bit-width remains a challenging problem. Here we present the Flexpoint data format, aiming at a complete replacement of 32-bit floating point format training and inference, designed to support modern deep network topologies without modifications. Flexpoint tensors have a shared exponent that is dynamically adjusted to minimize overflows and maximize available dynamic range. We validate Flexpoint by training AlexNet, a deep residual network and a generative adversarial network, using a simulator implemented with the neon deep learning framework. We demonstrate that 16-bit Flexpoint closely matches 32-bit floating point in training all three models, without any need for tuning of model hyperparameters. Our results suggest Flexpoint as a promising numerical format for future hardware for training and inference.

Application of Deep Convolutional Neural Networks for Detecting Extreme Weather in Climate Datasets

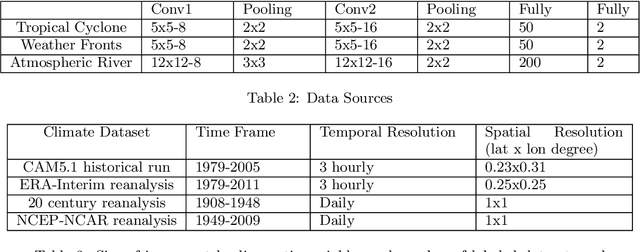
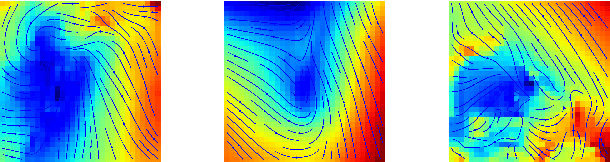
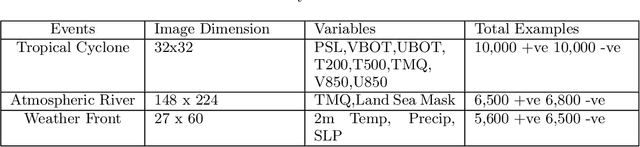
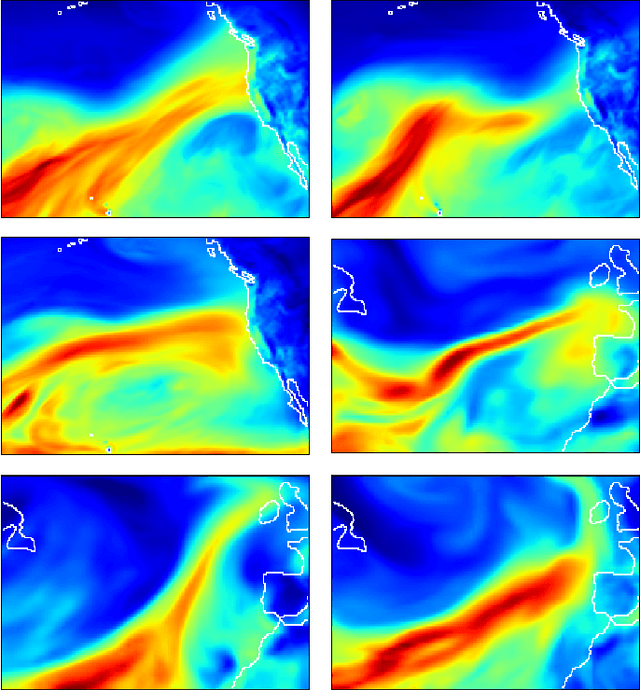
Detecting extreme events in large datasets is a major challenge in climate science research. Current algorithms for extreme event detection are build upon human expertise in defining events based on subjective thresholds of relevant physical variables. Often, multiple competing methods produce vastly different results on the same dataset. Accurate characterization of extreme events in climate simulations and observational data archives is critical for understanding the trends and potential impacts of such events in a climate change content. This study presents the first application of Deep Learning techniques as alternative methodology for climate extreme events detection. Deep neural networks are able to learn high-level representations of a broad class of patterns from labeled data. In this work, we developed deep Convolutional Neural Network (CNN) classification system and demonstrated the usefulness of Deep Learning technique for tackling climate pattern detection problems. Coupled with Bayesian based hyper-parameter optimization scheme, our deep CNN system achieves 89\%-99\% of accuracy in detecting extreme events (Tropical Cyclones, Atmospheric Rivers and Weather Fronts