Binding in hippocampal-entorhinal circuits enables compositionality in cognitive maps

We propose a normative model for spatial representation in the hippocampal formation that combines optimality principles, such as maximizing coding range and spatial information per neuron, with an algebraic framework for computing in distributed representation. Spatial position is encoded in a residue number system, with individual residues represented by high-dimensional, complex-valued vectors. These are composed into a single vector representing position by a similarity-preserving, conjunctive vector-binding operation. Self-consistency between the representations of the overall position and of the individual residues is enforced by a modular attractor network whose modules correspond to the grid cell modules in entorhinal cortex. The vector binding operation can also associate different contexts to spatial representations, yielding a model for entorhinal cortex and hippocampus. We show that the model achieves normative desiderata including superlinear scaling of patterns with dimension, robust error correction, and hexagonal, carry-free encoding of spatial position. These properties in turn enable robust path integration and association with sensory inputs. More generally, the model formalizes how compositional computations could occur in the hippocampal formation and leads to testable experimental predictions.

Compositional Factorization of Visual Scenes with Convolutional Sparse Coding and Resonator Networks

We propose a system for visual scene analysis and recognition based on encoding the sparse, latent feature-representation of an image into a high-dimensional vector that is subsequently factorized to parse scene content. The sparse feature representation is learned from image statistics via convolutional sparse coding, while scene parsing is performed by a resonator network. The integration of sparse coding with the resonator network increases the capacity of distributed representations and reduces collisions in the combinatorial search space during factorization. We find that for this problem the resonator network is capable of fast and accurate vector factorization, and we develop a confidence-based metric that assists in tracking the convergence of the resonator network.

Computing with Residue Numbers in High-Dimensional Representation

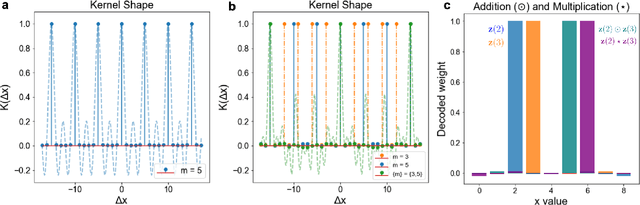
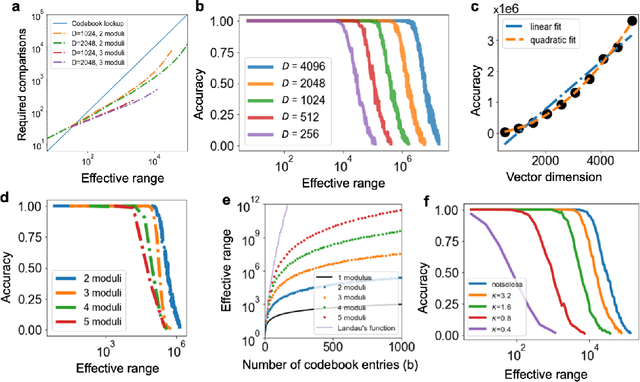
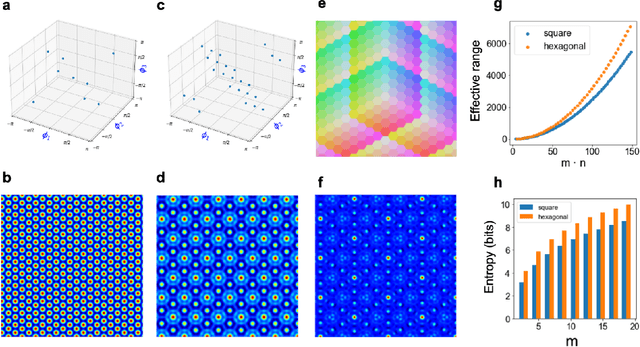
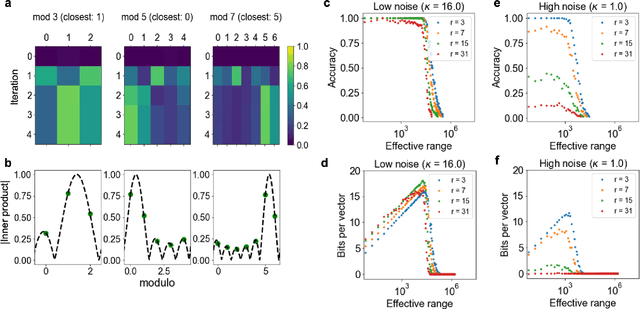
We introduce Residue Hyperdimensional Computing, a computing framework that unifies residue number systems with an algebra defined over random, high-dimensional vectors. We show how residue numbers can be represented as high-dimensional vectors in a manner that allows algebraic operations to be performed with component-wise, parallelizable operations on the vector elements. The resulting framework, when combined with an efficient method for factorizing high-dimensional vectors, can represent and operate on numerical values over a large dynamic range using vastly fewer resources than previous methods, and it exhibits impressive robustness to noise. We demonstrate the potential for this framework to solve computationally difficult problems in visual perception and combinatorial optimization, showing improvement over baseline methods. More broadly, the framework provides a possible account for the computational operations of grid cells in the brain, and it suggests new machine learning architectures for representing and manipulating numerical data.

Efficient Decoding of Compositional Structure in Holistic Representations

We investigate the task of retrieving information from compositional distributed representations formed by Hyperdimensional Computing/Vector Symbolic Architectures and present novel techniques which achieve new information rate bounds. First, we provide an overview of the decoding techniques that can be used to approach the retrieval task. The techniques are categorized into four groups. We then evaluate the considered techniques in several settings that involve, e.g., inclusion of external noise and storage elements with reduced precision. In particular, we find that the decoding techniques from the sparse coding and compressed sensing literature (rarely used for Hyperdimensional Computing/Vector Symbolic Architectures) are also well-suited for decoding information from the compositional distributed representations. Combining these decoding techniques with interference cancellation ideas from communications improves previously reported bounds (Hersche et al., 2021) of the information rate of the distributed representations from 1.20 to 1.40 bits per dimension for smaller codebooks and from 0.60 to 1.26 bits per dimension for larger codebooks.

Learning and generalization of compositional representations of visual scenes

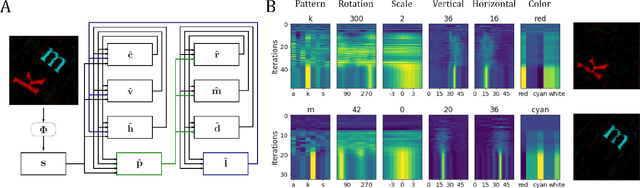
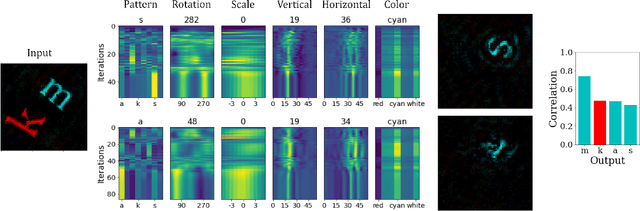
Complex visual scenes that are composed of multiple objects, each with attributes, such as object name, location, pose, color, etc., are challenging to describe in order to train neural networks. Usually,deep learning networks are trained supervised by categorical scene descriptions. The common categorical description of a scene contains the names of individual objects but lacks information about other attributes. Here, we use distributed representations of object attributes and vector operations in a vector symbolic architecture to create a full compositional description of a scene in a high-dimensional vector. To control the scene composition, we use artificial images composed of multiple, translated and colored MNIST digits. In contrast to learning category labels, here we train deep neural networks to output the full compositional vector description of an input image. The output of the deep network can then be interpreted by a VSA resonator network, to extract object identity or other properties of indiviual objects. We evaluate the performance and generalization properties of the system on randomly generated scenes. Specifically, we show that the network is able to learn the task and generalize to unseen seen digit shapes and scene configurations. Further, the generalisation ability of the trained model is limited. For example, with a gap in the training data, like an object not shown in a particular image location during training, the learning does not automatically fill this gap.

Efficient Optimization with Higher-Order Ising Machines

A prominent approach to solving combinatorial optimization problems on parallel hardware is Ising machines, i.e., hardware implementations of networks of interacting binary spin variables. Most Ising machines leverage second-order interactions although important classes of optimization problems, such as satisfiability problems, map more seamlessly to Ising networks with higher-order interactions. Here, we demonstrate that higher-order Ising machines can solve satisfiability problems more resource-efficiently in terms of the number of spin variables and their connections when compared to traditional second-order Ising machines. Further, our results show on a benchmark dataset of Boolean \textit{k}-satisfiability problems that higher-order Ising machines implemented with coupled oscillators rapidly find solutions that are better than second-order Ising machines, thus, improving the current state-of-the-art for Ising machines.

Computing with Hypervectors for Efficient Speaker Identification

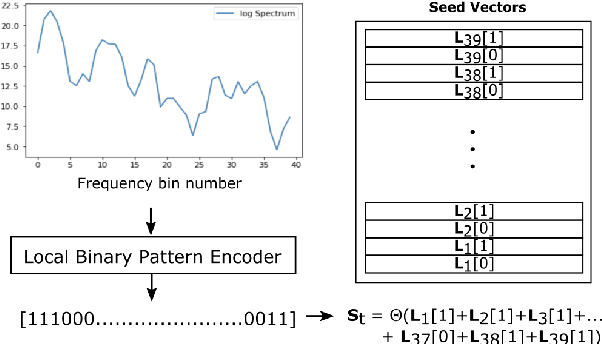
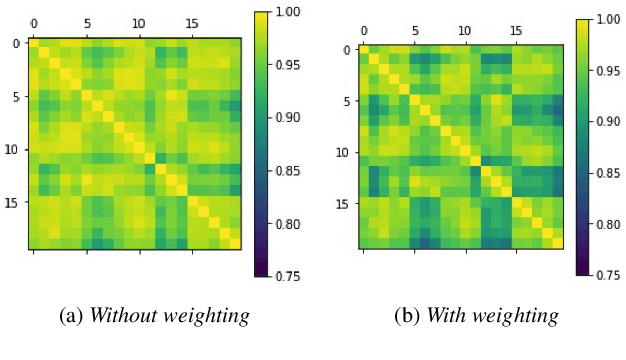
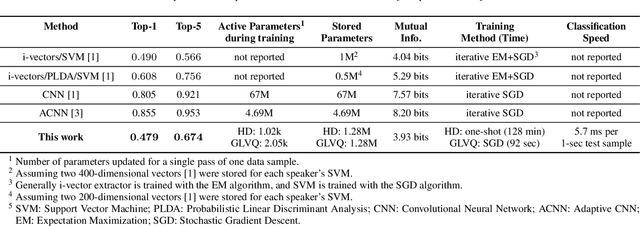
We introduce a method to identify speakers by computing with high-dimensional random vectors. Its strengths are simplicity and speed. With only 1.02k active parameters and a 128-minute pass through the training data we achieve Top-1 and Top-5 scores of 31% and 52% on the VoxCeleb1 dataset of 1,251 speakers. This is in contrast to CNN models requiring several million parameters and orders of magnitude higher computational complexity for only a 2$\times$ gain in discriminative power as measured in mutual information. An additional 92 seconds of training with Generalized Learning Vector Quantization (GLVQ) raises the scores to 48% and 67%. A trained classifier classifies 1 second of speech in 5.7 ms. All processing was done on standard CPU-based machines.

Neuromorphic Visual Scene Understanding with Resonator Networks

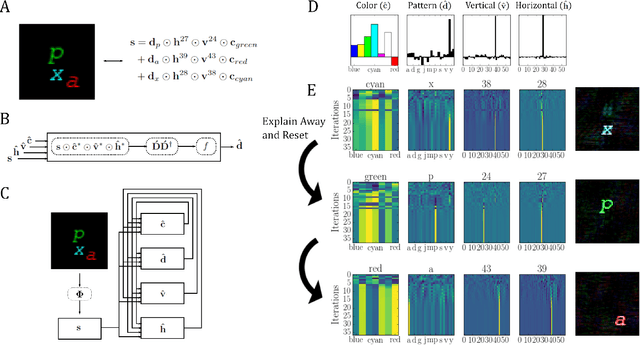
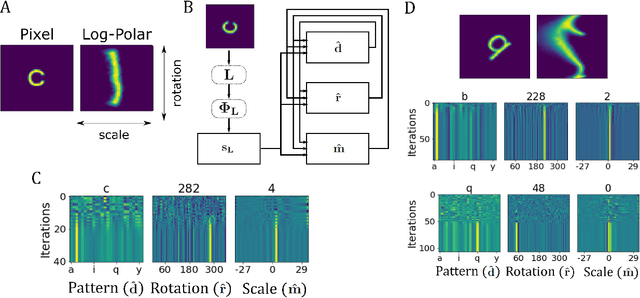
Inferring the position of objects and their rigid transformations is still an open problem in visual scene understanding. Here we propose a neuromorphic solution that utilizes an efficient factorization network which is based on three key concepts: (1) a computational framework based on Vector Symbolic Architectures (VSA) with complex-valued vectors; (2) the design of Hierarchical Resonator Networks (HRN) to deal with the non-commutative nature of translation and rotation in visual scenes, when both are used in combination; (3) the design of a multi-compartment spiking phasor neuron model for implementing complex-valued vector binding on neuromorphic hardware. The VSA framework uses vector binding operations to produce generative image models in which binding acts as the equivariant operation for geometric transformations. A scene can therefore be described as a sum of vector products, which in turn can be efficiently factorized by a resonator network to infer objects and their poses. The HRN enables the definition of a partitioned architecture in which vector binding is equivariant for horizontal and vertical translation within one partition, and for rotation and scaling within the other partition. The spiking neuron model allows to map the resonator network onto efficient and low-power neuromorphic hardware. In this work, we demonstrate our approach using synthetic scenes composed of simple 2D shapes undergoing rigid geometric transformations and color changes. A companion paper demonstrates this approach in real-world application scenarios for machine vision and robotics.

Learning and Inference in Sparse Coding Models with Langevin Dynamics

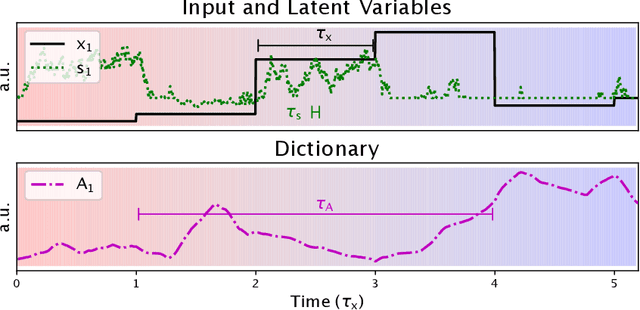
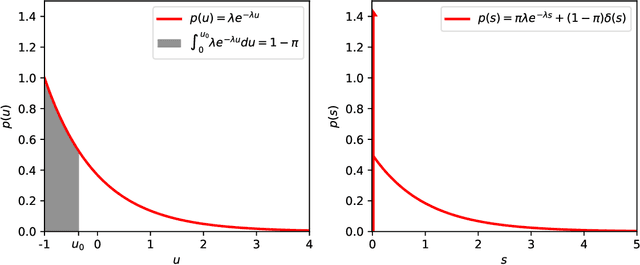
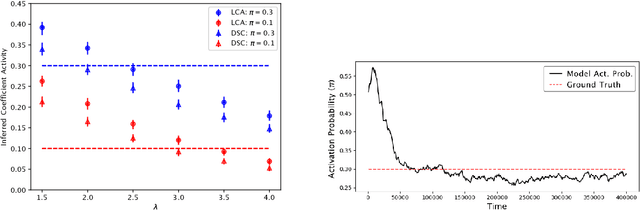
We describe a stochastic, dynamical system capable of inference and learning in a probabilistic latent variable model. The most challenging problem in such models - sampling the posterior distribution over latent variables - is proposed to be solved by harnessing natural sources of stochasticity inherent in electronic and neural systems. We demonstrate this idea for a sparse coding model by deriving a continuous-time equation for inferring its latent variables via Langevin dynamics. The model parameters are learned by simultaneously evolving according to another continuous-time equation, thus bypassing the need for digital accumulators or a global clock. Moreover we show that Langevin dynamics lead to an efficient procedure for sampling from the posterior distribution in the 'L0 sparse' regime, where latent variables are encouraged to be set to zero as opposed to having a small L1 norm. This allows the model to properly incorporate the notion of sparsity rather than having to resort to a relaxed version of sparsity to make optimization tractable. Simulations of the proposed dynamical system on both synthetic and natural image datasets demonstrate that the model is capable of probabilistically correct inference, enabling learning of the dictionary as well as parameters of the prior.

Integer Factorization with Compositional Distributed Representations

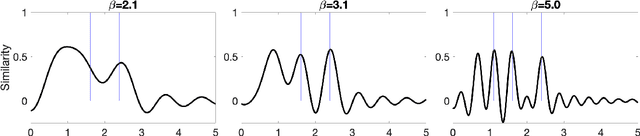
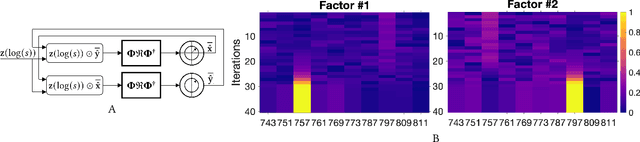
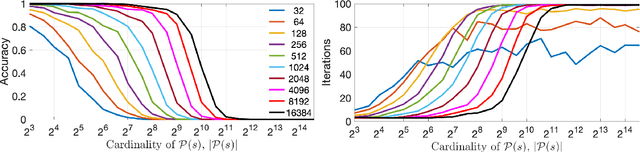
In this paper, we present an approach to integer factorization using distributed representations formed with Vector Symbolic Architectures. The approach formulates integer factorization in a manner such that it can be solved using neural networks and potentially implemented on parallel neuromorphic hardware. We introduce a method for encoding numbers in distributed vector spaces and explain how the resonator network can solve the integer factorization problem. We evaluate the approach on factorization of semiprimes by measuring the factorization accuracy versus the scale of the problem. We also demonstrate how the proposed approach generalizes beyond the factorization of semiprimes; in principle, it can be used for factorization of any composite number. This work demonstrates how a well-known combinatorial search problem may be formulated and solved within the framework of Vector Symbolic Architectures, and it opens the door to solving similarly difficult problems in other domains.