Binding in hippocampal-entorhinal circuits enables compositionality in cognitive maps

We propose a normative model for spatial representation in the hippocampal formation that combines optimality principles, such as maximizing coding range and spatial information per neuron, with an algebraic framework for computing in distributed representation. Spatial position is encoded in a residue number system, with individual residues represented by high-dimensional, complex-valued vectors. These are composed into a single vector representing position by a similarity-preserving, conjunctive vector-binding operation. Self-consistency between the representations of the overall position and of the individual residues is enforced by a modular attractor network whose modules correspond to the grid cell modules in entorhinal cortex. The vector binding operation can also associate different contexts to spatial representations, yielding a model for entorhinal cortex and hippocampus. We show that the model achieves normative desiderata including superlinear scaling of patterns with dimension, robust error correction, and hexagonal, carry-free encoding of spatial position. These properties in turn enable robust path integration and association with sensory inputs. More generally, the model formalizes how compositional computations could occur in the hippocampal formation and leads to testable experimental predictions.

Compositional Factorization of Visual Scenes with Convolutional Sparse Coding and Resonator Networks

We propose a system for visual scene analysis and recognition based on encoding the sparse, latent feature-representation of an image into a high-dimensional vector that is subsequently factorized to parse scene content. The sparse feature representation is learned from image statistics via convolutional sparse coding, while scene parsing is performed by a resonator network. The integration of sparse coding with the resonator network increases the capacity of distributed representations and reduces collisions in the combinatorial search space during factorization. We find that for this problem the resonator network is capable of fast and accurate vector factorization, and we develop a confidence-based metric that assists in tracking the convergence of the resonator network.

Computing with Residue Numbers in High-Dimensional Representation

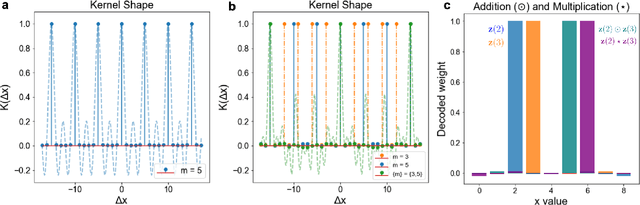
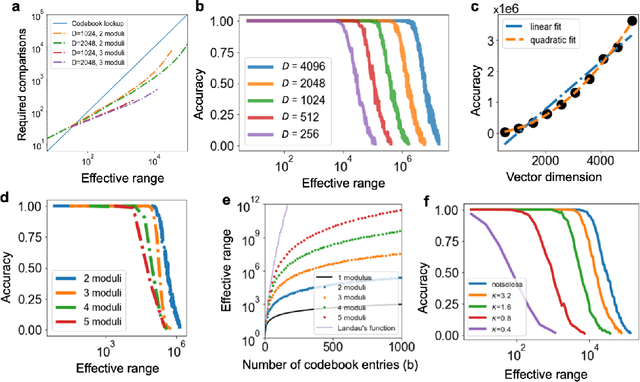
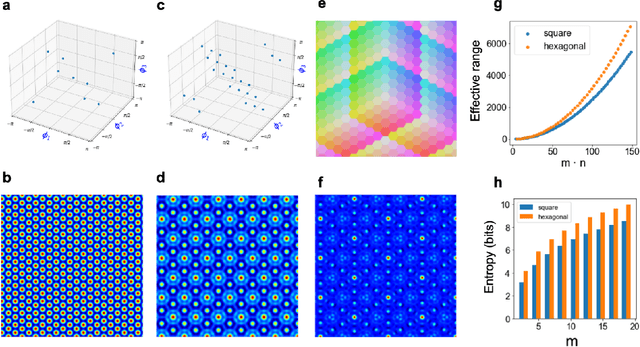
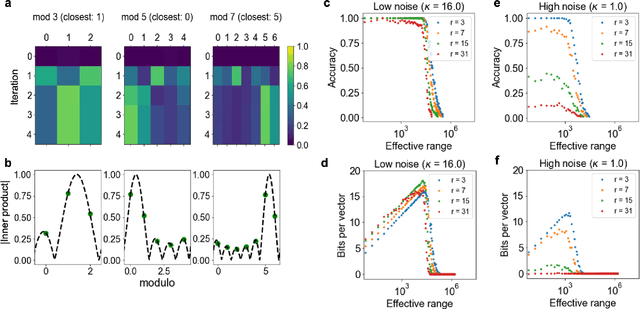
We introduce Residue Hyperdimensional Computing, a computing framework that unifies residue number systems with an algebra defined over random, high-dimensional vectors. We show how residue numbers can be represented as high-dimensional vectors in a manner that allows algebraic operations to be performed with component-wise, parallelizable operations on the vector elements. The resulting framework, when combined with an efficient method for factorizing high-dimensional vectors, can represent and operate on numerical values over a large dynamic range using vastly fewer resources than previous methods, and it exhibits impressive robustness to noise. We demonstrate the potential for this framework to solve computationally difficult problems in visual perception and combinatorial optimization, showing improvement over baseline methods. More broadly, the framework provides a possible account for the computational operations of grid cells in the brain, and it suggests new machine learning architectures for representing and manipulating numerical data.

Efficient Decoding of Compositional Structure in Holistic Representations

We investigate the task of retrieving information from compositional distributed representations formed by Hyperdimensional Computing/Vector Symbolic Architectures and present novel techniques which achieve new information rate bounds. First, we provide an overview of the decoding techniques that can be used to approach the retrieval task. The techniques are categorized into four groups. We then evaluate the considered techniques in several settings that involve, e.g., inclusion of external noise and storage elements with reduced precision. In particular, we find that the decoding techniques from the sparse coding and compressed sensing literature (rarely used for Hyperdimensional Computing/Vector Symbolic Architectures) are also well-suited for decoding information from the compositional distributed representations. Combining these decoding techniques with interference cancellation ideas from communications improves previously reported bounds (Hersche et al., 2021) of the information rate of the distributed representations from 1.20 to 1.40 bits per dimension for smaller codebooks and from 0.60 to 1.26 bits per dimension for larger codebooks.

Integer Factorization with Compositional Distributed Representations

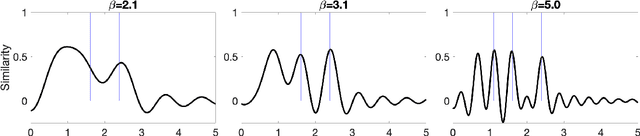
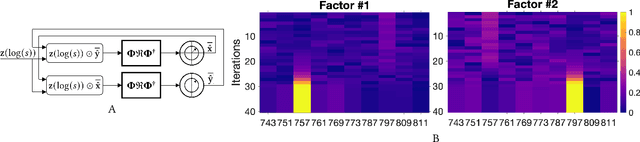
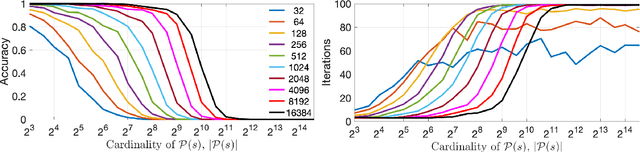
In this paper, we present an approach to integer factorization using distributed representations formed with Vector Symbolic Architectures. The approach formulates integer factorization in a manner such that it can be solved using neural networks and potentially implemented on parallel neuromorphic hardware. We introduce a method for encoding numbers in distributed vector spaces and explain how the resonator network can solve the integer factorization problem. We evaluate the approach on factorization of semiprimes by measuring the factorization accuracy versus the scale of the problem. We also demonstrate how the proposed approach generalizes beyond the factorization of semiprimes; in principle, it can be used for factorization of any composite number. This work demonstrates how a well-known combinatorial search problem may be formulated and solved within the framework of Vector Symbolic Architectures, and it opens the door to solving similarly difficult problems in other domains.

Computing on Functions Using Randomized Vector Representations

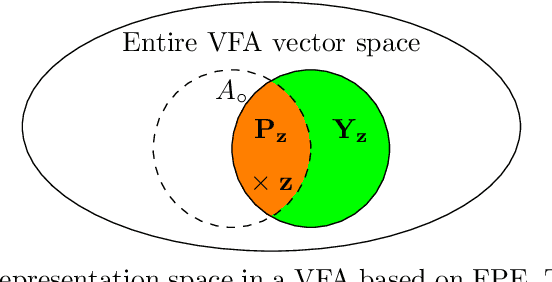
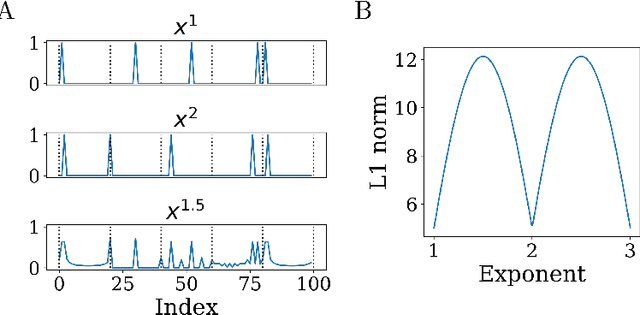
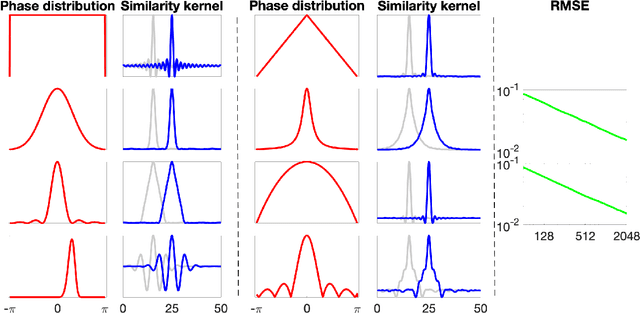
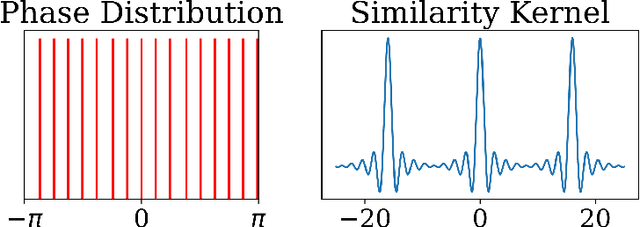
Vector space models for symbolic processing that encode symbols by random vectors have been proposed in cognitive science and connectionist communities under the names Vector Symbolic Architecture (VSA), and, synonymously, Hyperdimensional (HD) computing. In this paper, we generalize VSAs to function spaces by mapping continuous-valued data into a vector space such that the inner product between the representations of any two data points represents a similarity kernel. By analogy to VSA, we call this new function encoding and computing framework Vector Function Architecture (VFA). In VFAs, vectors can represent individual data points as well as elements of a function space (a reproducing kernel Hilbert space). The algebraic vector operations, inherited from VSA, correspond to well-defined operations in function space. Furthermore, we study a previously proposed method for encoding continuous data, fractional power encoding (FPE), which uses exponentiation of a random base vector to produce randomized representations of data points and fulfills the kernel properties for inducing a VFA. We show that the distribution from which elements of the base vector are sampled determines the shape of the FPE kernel, which in turn induces a VFA for computing with band-limited functions. In particular, VFAs provide an algebraic framework for implementing large-scale kernel machines with random features, extending Rahimi and Recht, 2007. Finally, we demonstrate several applications of VFA models to problems in image recognition, density estimation and nonlinear regression. Our analyses and results suggest that VFAs constitute a powerful new framework for representing and manipulating functions in distributed neural systems, with myriad applications in artificial intelligence.