Autonomous Learning with High-Dimensional Computing Architecture Similar to von Neumann's

We model human and animal learning by computing with high-dimensional vectors (H = 10,000 for example). The architecture resembles traditional (von Neumann) computing with numbers, but the instructions refer to vectors and operate on them in superposition. The architecture includes a high-capacity memory for vectors, analogue of the random-access memory (RAM) for numbers. The model's ability to learn from data reminds us of deep learning, but with an architecture closer to biology. The architecture agrees with an idea from psychology that human memory and learning involve a short-term working memory and a long-term data store. Neuroscience provides us with a model of the long-term memory, namely, the cortex of the cerebellum. With roots in psychology, biology, and traditional computing, a theory of computing with vectors can help us understand how brains compute. Application to learning by robots seems inevitable, but there is likely to be more, including language. Ultimately we want to compute with no more material and energy than used by brains. To that end, we need a mathematical theory that agrees with psychology and biology, and is suitable for nanotechnology. We also need to exercise the theory in large-scale experiments. Computing with vectors is described here in terms familiar to us from traditional computing with numbers.

Computing with Residue Numbers in High-Dimensional Representation

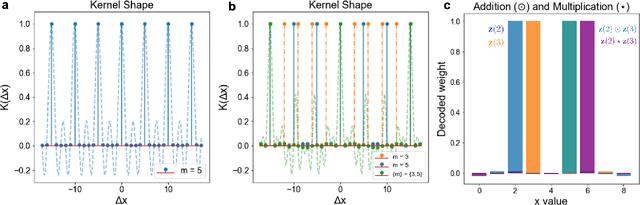
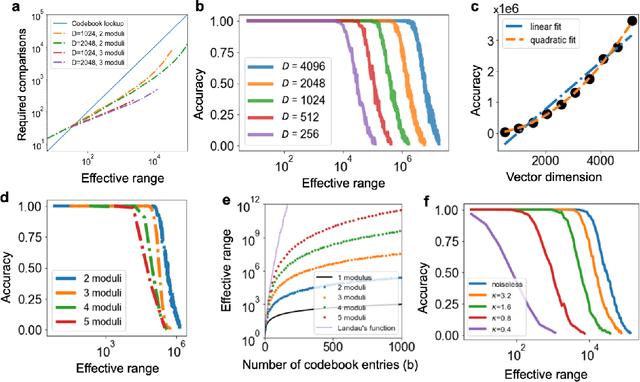
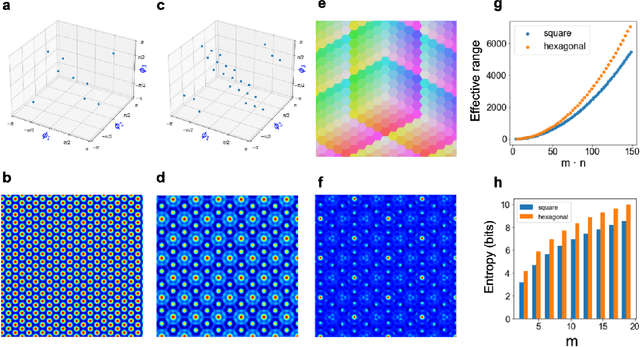
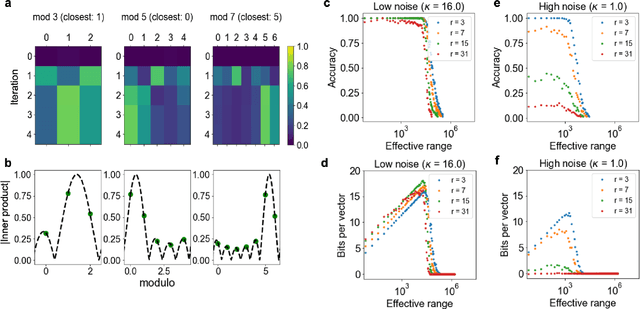
We introduce Residue Hyperdimensional Computing, a computing framework that unifies residue number systems with an algebra defined over random, high-dimensional vectors. We show how residue numbers can be represented as high-dimensional vectors in a manner that allows algebraic operations to be performed with component-wise, parallelizable operations on the vector elements. The resulting framework, when combined with an efficient method for factorizing high-dimensional vectors, can represent and operate on numerical values over a large dynamic range using vastly fewer resources than previous methods, and it exhibits impressive robustness to noise. We demonstrate the potential for this framework to solve computationally difficult problems in visual perception and combinatorial optimization, showing improvement over baseline methods. More broadly, the framework provides a possible account for the computational operations of grid cells in the brain, and it suggests new machine learning architectures for representing and manipulating numerical data.

Learning and generalization of compositional representations of visual scenes

Complex visual scenes that are composed of multiple objects, each with attributes, such as object name, location, pose, color, etc., are challenging to describe in order to train neural networks. Usually,deep learning networks are trained supervised by categorical scene descriptions. The common categorical description of a scene contains the names of individual objects but lacks information about other attributes. Here, we use distributed representations of object attributes and vector operations in a vector symbolic architecture to create a full compositional description of a scene in a high-dimensional vector. To control the scene composition, we use artificial images composed of multiple, translated and colored MNIST digits. In contrast to learning category labels, here we train deep neural networks to output the full compositional vector description of an input image. The output of the deep network can then be interpreted by a VSA resonator network, to extract object identity or other properties of indiviual objects. We evaluate the performance and generalization properties of the system on randomly generated scenes. Specifically, we show that the network is able to learn the task and generalize to unseen seen digit shapes and scene configurations. Further, the generalisation ability of the trained model is limited. For example, with a gap in the training data, like an object not shown in a particular image location during training, the learning does not automatically fill this gap.

Computing with Hypervectors for Efficient Speaker Identification

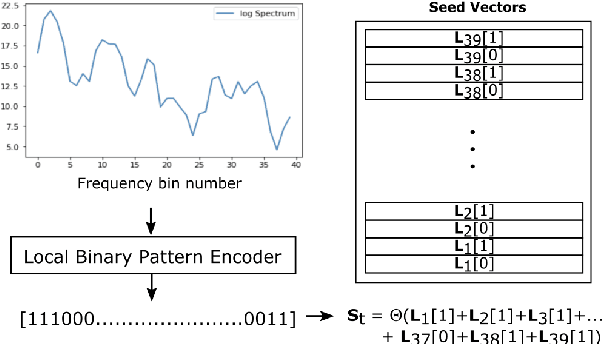
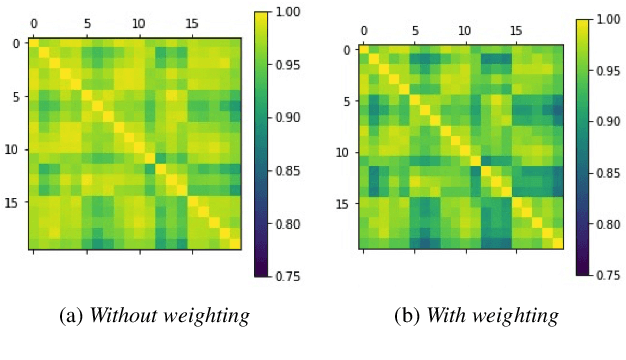
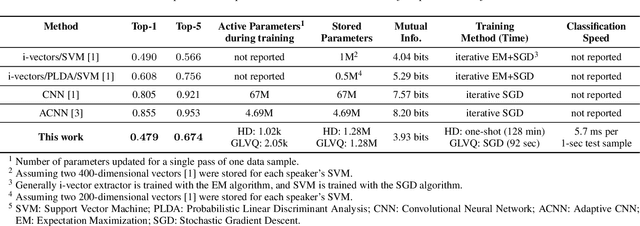
We introduce a method to identify speakers by computing with high-dimensional random vectors. Its strengths are simplicity and speed. With only 1.02k active parameters and a 128-minute pass through the training data we achieve Top-1 and Top-5 scores of 31% and 52% on the VoxCeleb1 dataset of 1,251 speakers. This is in contrast to CNN models requiring several million parameters and orders of magnitude higher computational complexity for only a 2$\times$ gain in discriminative power as measured in mutual information. An additional 92 seconds of training with Generalized Learning Vector Quantization (GLVQ) raises the scores to 48% and 67%. A trained classifier classifies 1 second of speech in 5.7 ms. All processing was done on standard CPU-based machines.

Vector Symbolic Architectures as a Computing Framework for Nanoscale Hardware

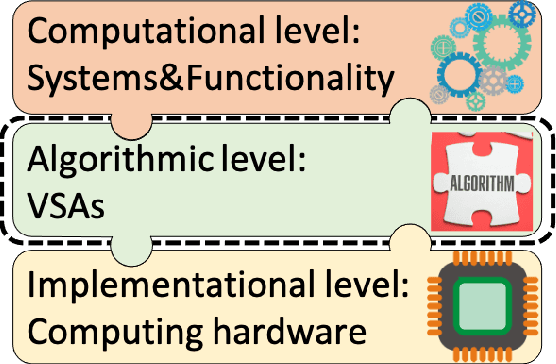
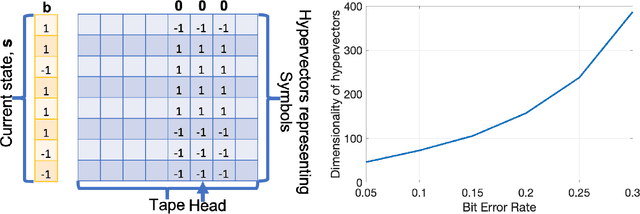
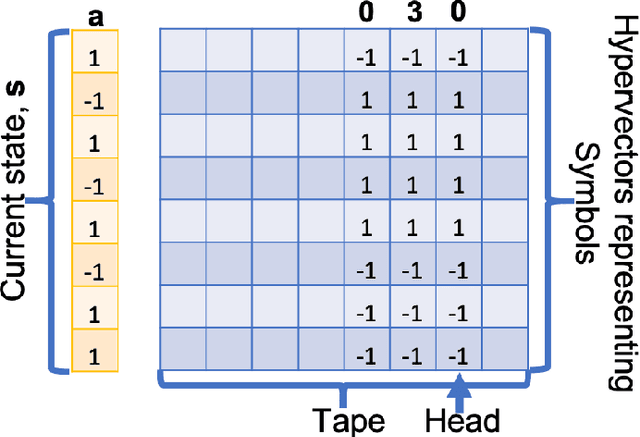
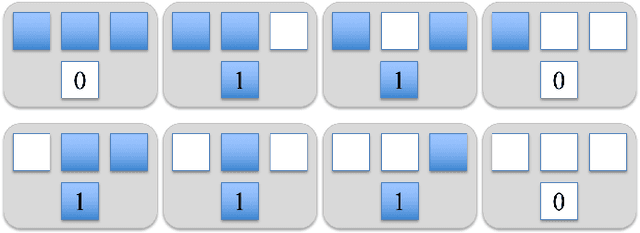
This article reviews recent progress in the development of the computing framework Vector Symbolic Architectures (also known as Hyperdimensional Computing). This framework is well suited for implementation in stochastic, nanoscale hardware and it naturally expresses the types of cognitive operations required for Artificial Intelligence (AI). We demonstrate in this article that the ring-like algebraic structure of Vector Symbolic Architectures offers simple but powerful operations on high-dimensional vectors that can support all data structures and manipulations relevant in modern computing. In addition, we illustrate the distinguishing feature of Vector Symbolic Architectures, "computing in superposition," which sets it apart from conventional computing. This latter property opens the door to efficient solutions to the difficult combinatorial search problems inherent in AI applications. Vector Symbolic Architectures are Turing complete, as we show, and we see them acting as a framework for computing with distributed representations in myriad AI settings. This paper serves as a reference for computer architects by illustrating techniques and philosophy of VSAs for distributed computing and relevance to emerging computing hardware, such as neuromorphic computing.

High-dimensional distributed semantic spaces for utterances

High-dimensional distributed semantic spaces have proven useful and effective for aggregating and processing visual, auditory, and lexical information for many tasks related to human-generated data. Human language makes use of a large and varying number of features, lexical and constructional items as well as contextual and discourse-specific data of various types, which all interact to represent various aspects of communicative information. Some of these features are mostly local and useful for the organisation of e.g. argument structure of a predication; others are persistent over the course of a discourse and necessary for achieving a reasonable level of understanding of the content. This paper describes a model for high-dimensional representation for utterance and text level data including features such as constructions or contextual data, based on a mathematically principled and behaviourally plausible approach to representing linguistic information. The implementation of the representation is a straightforward extension of Random Indexing models previously used for lexical linguistic items. The paper shows how the implemented model is able to represent a broad range of linguistic features in a common integral framework of fixed dimensionality, which is computationally habitable, and which is suitable as a bridge between symbolic representations such as dependency analysis and continuous representations used e.g. in classifiers or further machine-learning approaches. This is achieved with operations on vectors that constitute a powerful computational algebra, accompanied with an associative memory for the vectors. The paper provides a technical overview of the framework and a worked through implemented example of how it can be applied to various types of linguistic features.

Language Recognition using Random Indexing

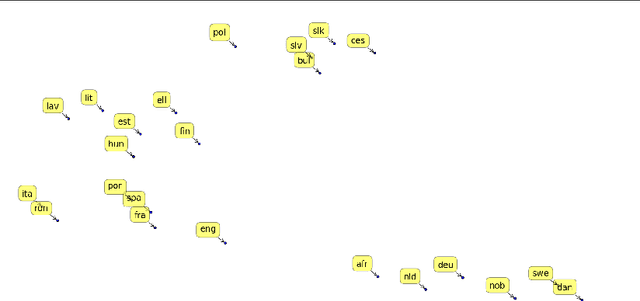
Random Indexing is a simple implementation of Random Projections with a wide range of applications. It can solve a variety of problems with good accuracy without introducing much complexity. Here we use it for identifying the language of text samples. We present a novel method of generating language representation vectors using letter blocks. Further, we show that the method is easily implemented and requires little computational power and space. Experiments on a number of model parameters illustrate certain properties about high dimensional sparse vector representations of data. Proof of statistically relevant language vectors are shown through the extremely high success of various language recognition tasks. On a difficult data set of 21,000 short sentences from 21 different languages, our model performs a language recognition task and achieves 97.8% accuracy, comparable to state-of-the-art methods.