Learning and generalization of compositional representations of visual scenes

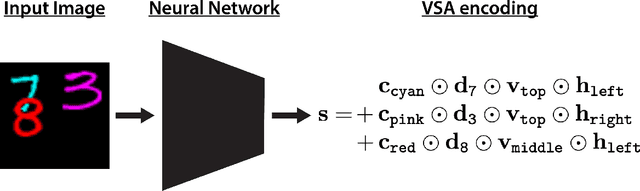
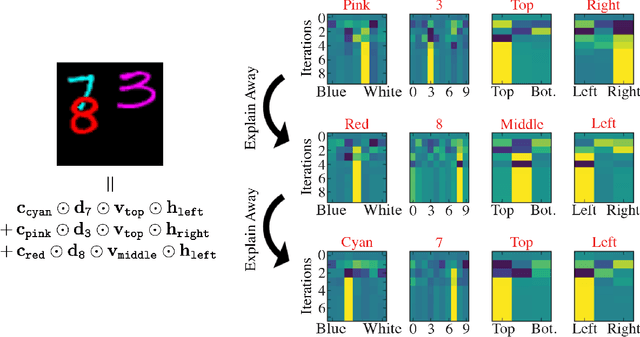
Complex visual scenes that are composed of multiple objects, each with attributes, such as object name, location, pose, color, etc., are challenging to describe in order to train neural networks. Usually,deep learning networks are trained supervised by categorical scene descriptions. The common categorical description of a scene contains the names of individual objects but lacks information about other attributes. Here, we use distributed representations of object attributes and vector operations in a vector symbolic architecture to create a full compositional description of a scene in a high-dimensional vector. To control the scene composition, we use artificial images composed of multiple, translated and colored MNIST digits. In contrast to learning category labels, here we train deep neural networks to output the full compositional vector description of an input image. The output of the deep network can then be interpreted by a VSA resonator network, to extract object identity or other properties of indiviual objects. We evaluate the performance and generalization properties of the system on randomly generated scenes. Specifically, we show that the network is able to learn the task and generalize to unseen seen digit shapes and scene configurations. Further, the generalisation ability of the trained model is limited. For example, with a gap in the training data, like an object not shown in a particular image location during training, the learning does not automatically fill this gap.

Resonator networks for factoring distributed representations of data structures

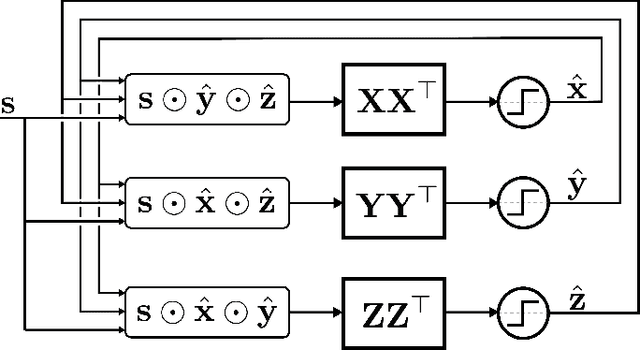
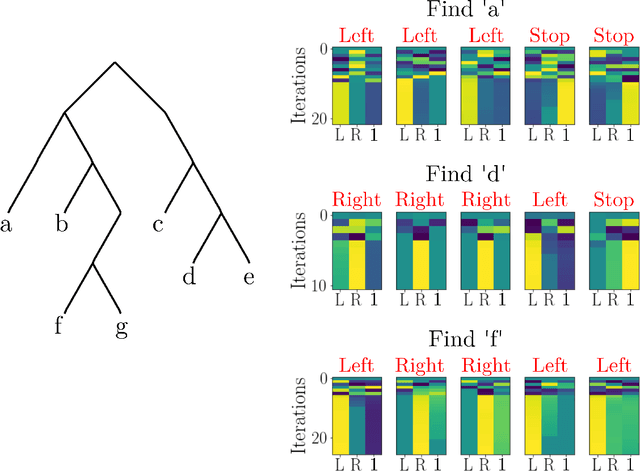
The ability to encode and manipulate data structures with distributed neural representations could qualitatively enhance the capabilities of traditional neural networks by supporting rule-based symbolic reasoning, a central property of cognition. Here we show how this may be accomplished within the framework of Vector Symbolic Architectures (VSA) (Plate, 1991; Gayler, 1998; Kanerva, 1996), whereby data structures are encoded by combining high-dimensional vectors with operations that together form an algebra on the space of distributed representations. In particular, we propose an efficient solution to a hard combinatorial search problem that arises when decoding elements of a VSA data structure: the factorization of products of multiple code vectors. Our proposed algorithm, called a resonator network, is a new type of recurrent neural network that interleaves VSA multiplication operations and pattern completion. We show in two examples -- parsing of a tree-like data structure and parsing of a visual scene -- how the factorization problem arises and how the resonator network can solve it. More broadly, resonator networks open the possibility to apply VSAs to myriad artificial intelligence problems in real-world domains. A companion paper (Kent et al., 2020) presents a rigorous analysis and evaluation of the performance of resonator networks, showing it out-performs alternative approaches.