Binding in hippocampal-entorhinal circuits enables compositionality in cognitive maps

We propose a normative model for spatial representation in the hippocampal formation that combines optimality principles, such as maximizing coding range and spatial information per neuron, with an algebraic framework for computing in distributed representation. Spatial position is encoded in a residue number system, with individual residues represented by high-dimensional, complex-valued vectors. These are composed into a single vector representing position by a similarity-preserving, conjunctive vector-binding operation. Self-consistency between the representations of the overall position and of the individual residues is enforced by a modular attractor network whose modules correspond to the grid cell modules in entorhinal cortex. The vector binding operation can also associate different contexts to spatial representations, yielding a model for entorhinal cortex and hippocampus. We show that the model achieves normative desiderata including superlinear scaling of patterns with dimension, robust error correction, and hexagonal, carry-free encoding of spatial position. These properties in turn enable robust path integration and association with sensory inputs. More generally, the model formalizes how compositional computations could occur in the hippocampal formation and leads to testable experimental predictions.

Computing with Residue Numbers in High-Dimensional Representation

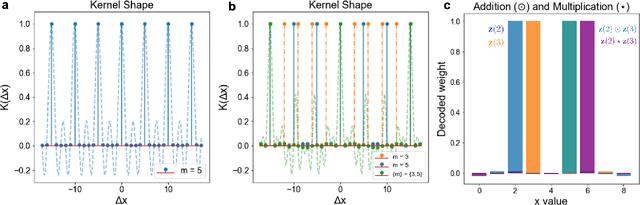
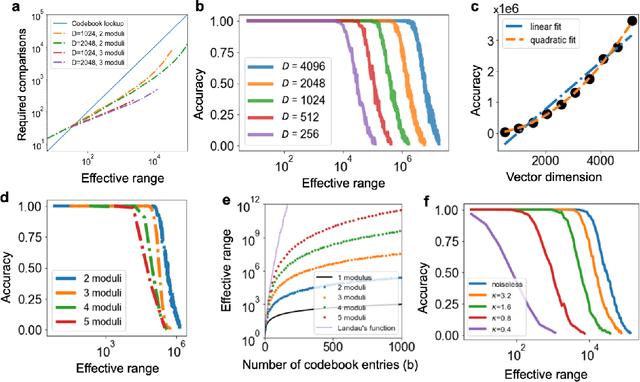
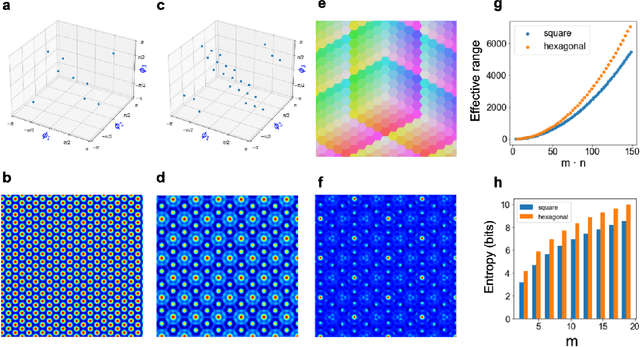
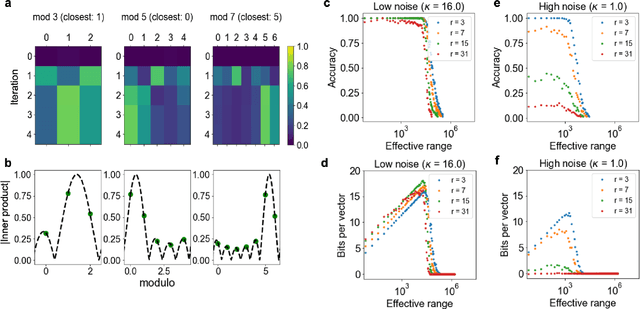
We introduce Residue Hyperdimensional Computing, a computing framework that unifies residue number systems with an algebra defined over random, high-dimensional vectors. We show how residue numbers can be represented as high-dimensional vectors in a manner that allows algebraic operations to be performed with component-wise, parallelizable operations on the vector elements. The resulting framework, when combined with an efficient method for factorizing high-dimensional vectors, can represent and operate on numerical values over a large dynamic range using vastly fewer resources than previous methods, and it exhibits impressive robustness to noise. We demonstrate the potential for this framework to solve computationally difficult problems in visual perception and combinatorial optimization, showing improvement over baseline methods. More broadly, the framework provides a possible account for the computational operations of grid cells in the brain, and it suggests new machine learning architectures for representing and manipulating numerical data.

Efficient Decoding of Compositional Structure in Holistic Representations

We investigate the task of retrieving information from compositional distributed representations formed by Hyperdimensional Computing/Vector Symbolic Architectures and present novel techniques which achieve new information rate bounds. First, we provide an overview of the decoding techniques that can be used to approach the retrieval task. The techniques are categorized into four groups. We then evaluate the considered techniques in several settings that involve, e.g., inclusion of external noise and storage elements with reduced precision. In particular, we find that the decoding techniques from the sparse coding and compressed sensing literature (rarely used for Hyperdimensional Computing/Vector Symbolic Architectures) are also well-suited for decoding information from the compositional distributed representations. Combining these decoding techniques with interference cancellation ideas from communications improves previously reported bounds (Hersche et al., 2021) of the information rate of the distributed representations from 1.20 to 1.40 bits per dimension for smaller codebooks and from 0.60 to 1.26 bits per dimension for larger codebooks.

Learning and generalization of compositional representations of visual scenes

Complex visual scenes that are composed of multiple objects, each with attributes, such as object name, location, pose, color, etc., are challenging to describe in order to train neural networks. Usually,deep learning networks are trained supervised by categorical scene descriptions. The common categorical description of a scene contains the names of individual objects but lacks information about other attributes. Here, we use distributed representations of object attributes and vector operations in a vector symbolic architecture to create a full compositional description of a scene in a high-dimensional vector. To control the scene composition, we use artificial images composed of multiple, translated and colored MNIST digits. In contrast to learning category labels, here we train deep neural networks to output the full compositional vector description of an input image. The output of the deep network can then be interpreted by a VSA resonator network, to extract object identity or other properties of indiviual objects. We evaluate the performance and generalization properties of the system on randomly generated scenes. Specifically, we show that the network is able to learn the task and generalize to unseen seen digit shapes and scene configurations. Further, the generalisation ability of the trained model is limited. For example, with a gap in the training data, like an object not shown in a particular image location during training, the learning does not automatically fill this gap.

Efficient Optimization with Higher-Order Ising Machines

A prominent approach to solving combinatorial optimization problems on parallel hardware is Ising machines, i.e., hardware implementations of networks of interacting binary spin variables. Most Ising machines leverage second-order interactions although important classes of optimization problems, such as satisfiability problems, map more seamlessly to Ising networks with higher-order interactions. Here, we demonstrate that higher-order Ising machines can solve satisfiability problems more resource-efficiently in terms of the number of spin variables and their connections when compared to traditional second-order Ising machines. Further, our results show on a benchmark dataset of Boolean \textit{k}-satisfiability problems that higher-order Ising machines implemented with coupled oscillators rapidly find solutions that are better than second-order Ising machines, thus, improving the current state-of-the-art for Ising machines.

Neuromorphic Visual Odometry with Resonator Networks

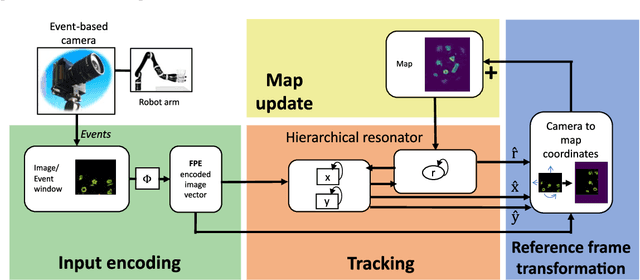
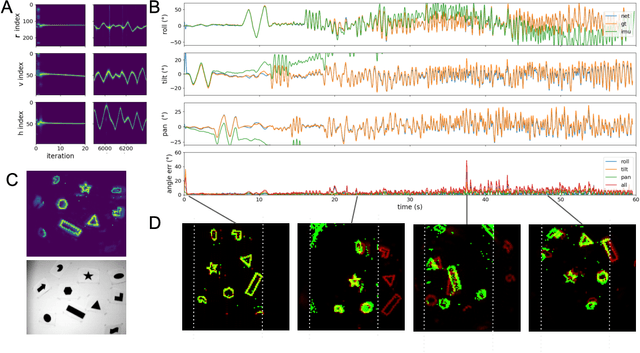
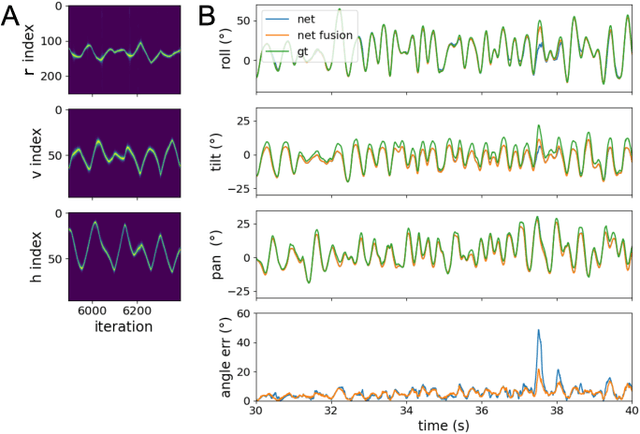
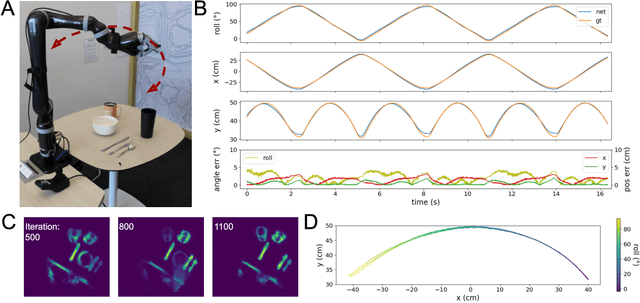
Autonomous agents require self-localization to navigate in unknown environments. They can use Visual Odometry (VO) to estimate self-motion and localize themselves using visual sensors. This motion-estimation strategy is not compromised by drift as inertial sensors or slippage as wheel encoders. However, VO with conventional cameras is computationally demanding, limiting its application in systems with strict low-latency, -memory, and -energy requirements. Using event-based cameras and neuromorphic computing hardware offers a promising low-power solution to the VO problem. However, conventional algorithms for VO are not readily convertible to neuromorphic hardware. In this work, we present a VO algorithm built entirely of neuronal building blocks suitable for neuromorphic implementation. The building blocks are groups of neurons representing vectors in the computational framework of Vector Symbolic Architecture (VSA) which was proposed as an abstraction layer to program neuromorphic hardware. The VO network we propose generates and stores a working memory of the presented visual environment. It updates this working memory while at the same time estimating the changing location and orientation of the camera. We demonstrate how VSA can be leveraged as a computing paradigm for neuromorphic robotics. Moreover, our results represent an important step towards using neuromorphic computing hardware for fast and power-efficient VO and the related task of simultaneous localization and mapping (SLAM). We validate this approach experimentally in a robotic task and with an event-based dataset, demonstrating state-of-the-art performance.

Neuromorphic Visual Scene Understanding with Resonator Networks

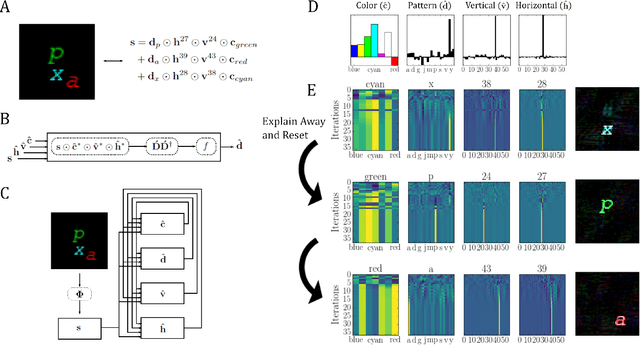
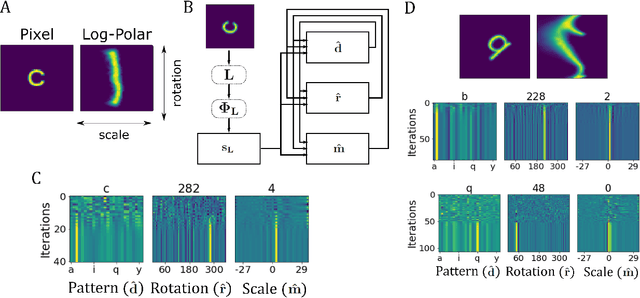
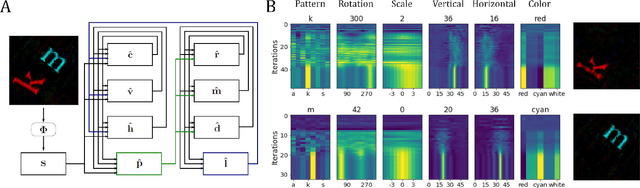
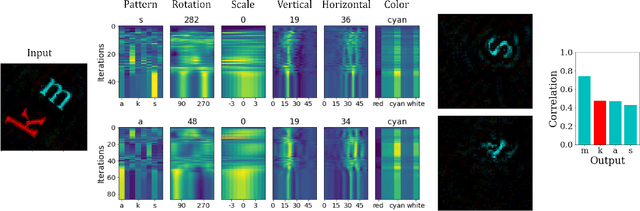
Inferring the position of objects and their rigid transformations is still an open problem in visual scene understanding. Here we propose a neuromorphic solution that utilizes an efficient factorization network which is based on three key concepts: (1) a computational framework based on Vector Symbolic Architectures (VSA) with complex-valued vectors; (2) the design of Hierarchical Resonator Networks (HRN) to deal with the non-commutative nature of translation and rotation in visual scenes, when both are used in combination; (3) the design of a multi-compartment spiking phasor neuron model for implementing complex-valued vector binding on neuromorphic hardware. The VSA framework uses vector binding operations to produce generative image models in which binding acts as the equivariant operation for geometric transformations. A scene can therefore be described as a sum of vector products, which in turn can be efficiently factorized by a resonator network to infer objects and their poses. The HRN enables the definition of a partitioned architecture in which vector binding is equivariant for horizontal and vertical translation within one partition, and for rotation and scaling within the other partition. The spiking neuron model allows to map the resonator network onto efficient and low-power neuromorphic hardware. In this work, we demonstrate our approach using synthetic scenes composed of simple 2D shapes undergoing rigid geometric transformations and color changes. A companion paper demonstrates this approach in real-world application scenarios for machine vision and robotics.

Cross-Frequency Coupling Increases Memory Capacity in Oscillatory Neural Networks

An open problem in neuroscience is to explain the functional role of oscillations in neural networks, contributing, for example, to perception, attention, and memory. Cross-frequency coupling (CFC) is associated with information integration across populations of neurons. Impaired CFC is linked to neurological disease. It is unclear what role CFC has in information processing and brain functional connectivity. We construct a model of CFC which predicts a computational role for observed $\theta - \gamma$ oscillatory circuits in the hippocampus and cortex. Our model predicts that the complex dynamics in recurrent and feedforward networks of coupled oscillators performs robust information storage and pattern retrieval. Based on phasor associative memories (PAM), we present a novel oscillator neural network (ONN) model that includes subharmonic injection locking (SHIL) and which reproduces experimental observations of CFC. We show that the presence of CFC increases the memory capacity of a population of neurons connected by plastic synapses. CFC enables error-free pattern retrieval whereas pattern retrieval fails without CFC. In addition, the trade-offs between sparse connectivity, capacity, and information per connection are identified. The associative memory is based on a complex-valued neural network, or phasor neural network (PNN). We show that for values of $Q$ which are the same as the ratio of $\gamma$ to $\theta$ oscillations observed in the hippocampus and the cortex, the associative memory achieves greater capacity and information storage than previous models. The novel contributions of this work are providing a computational framework based on oscillator dynamics which predicts the functional role of neural oscillations and connecting concepts in neural network theory and dynamical system theory.

Deep Learning in Spiking Phasor Neural Networks

Spiking Neural Networks (SNNs) have attracted the attention of the deep learning community for use in low-latency, low-power neuromorphic hardware, as well as models for understanding neuroscience. In this paper, we introduce Spiking Phasor Neural Networks (SPNNs). SPNNs are based on complex-valued Deep Neural Networks (DNNs), representing phases by spike times. Our model computes robustly employing a spike timing code and gradients can be formed using the complex domain. We train SPNNs on CIFAR-10, and demonstrate that the performance exceeds that of other timing coded SNNs, approaching results with comparable real-valued DNNs.

Integer Factorization with Compositional Distributed Representations

In this paper, we present an approach to integer factorization using distributed representations formed with Vector Symbolic Architectures. The approach formulates integer factorization in a manner such that it can be solved using neural networks and potentially implemented on parallel neuromorphic hardware. We introduce a method for encoding numbers in distributed vector spaces and explain how the resonator network can solve the integer factorization problem. We evaluate the approach on factorization of semiprimes by measuring the factorization accuracy versus the scale of the problem. We also demonstrate how the proposed approach generalizes beyond the factorization of semiprimes; in principle, it can be used for factorization of any composite number. This work demonstrates how a well-known combinatorial search problem may be formulated and solved within the framework of Vector Symbolic Architectures, and it opens the door to solving similarly difficult problems in other domains.