Towards a Comprehensive Theory of Reservoir Computing

In reservoir computing, an input sequence is processed by a recurrent neural network, the reservoir, which transforms it into a spatial pattern that a shallow readout network can then exploit for tasks such as memorization and time-series prediction or classification. Echo state networks (ESN) are a model class in which the reservoir is a traditional artificial neural network. This class contains many model types, each with sets of hyperparameters. Selecting models and parameter settings for particular applications requires a theory for predicting and comparing performances. Here, we demonstrate that recent developments of perceptron theory can be used to predict the memory capacity and accuracy of a wide variety of ESN models, including reservoirs with linear neurons, sigmoid nonlinear neurons, different types of recurrent matrices, and different types of readout networks. Across thirty variants of ESNs, we show that empirical results consistently confirm the theory's predictions. As a practical demonstration, the theory is used to optimize memory capacity of an ESN in the entire joint parameter space. Further, guided by the theory, we propose a novel ESN model with a readout network that does not require training, and which outperforms earlier ESN models without training. Finally, we characterize the geometry of the readout networks in ESNs, which reveals that many ESN models exhibit a similar regular simplex geometry as has been observed in the output weights of deep neural networks.

Efficient Hyperdimensional Computing with Modular Composite Representations

The modular composite representation (MCR) is a computing model that represents information with high-dimensional integer vectors using modular arithmetic. Originally proposed as a generalization of the binary spatter code model, it aims to provide higher representational power while remaining a lighter alternative to models requiring high-precision components. Despite this potential, MCR has received limited attention. Systematic analyses of its trade-offs and comparisons with other models are lacking, sustaining the perception that its added complexity outweighs the improved expressivity. In this work, we revisit MCR by presenting its first extensive evaluation, demonstrating that it achieves a unique balance of capacity, accuracy, and hardware efficiency. Experiments measuring capacity demonstrate that MCR outperforms binary and integer vectors while approaching complex-valued representations at a fraction of their memory footprint. Evaluation on 123 datasets confirms consistent accuracy gains and shows that MCR can match the performance of binary spatter codes using up to 4x less memory. We investigate the hardware realization of MCR by showing that it maps naturally to digital logic and by designing the first dedicated accelerator. Evaluations on basic operations and 7 selected datasets demonstrate a speedup of up to 3 orders of magnitude and significant energy reductions compared to software implementation. When matched for accuracy against binary spatter codes, MCR achieves on average 3.08x faster execution and 2.68x lower energy consumption. These findings demonstrate that, although MCR requires more sophisticated operations than binary spatter codes, its modular arithmetic and higher per-component precision enable lower dimensionality. When realized with dedicated hardware, this results in a faster, more energy-efficient, and high-precision alternative to existing models.

Binding in hippocampal-entorhinal circuits enables compositionality in cognitive maps

We propose a normative model for spatial representation in the hippocampal formation that combines optimality principles, such as maximizing coding range and spatial information per neuron, with an algebraic framework for computing in distributed representation. Spatial position is encoded in a residue number system, with individual residues represented by high-dimensional, complex-valued vectors. These are composed into a single vector representing position by a similarity-preserving, conjunctive vector-binding operation. Self-consistency between the representations of the overall position and of the individual residues is enforced by a modular attractor network whose modules correspond to the grid cell modules in entorhinal cortex. The vector binding operation can also associate different contexts to spatial representations, yielding a model for entorhinal cortex and hippocampus. We show that the model achieves normative desiderata including superlinear scaling of patterns with dimension, robust error correction, and hexagonal, carry-free encoding of spatial position. These properties in turn enable robust path integration and association with sensory inputs. More generally, the model formalizes how compositional computations could occur in the hippocampal formation and leads to testable experimental predictions.

Compositional Factorization of Visual Scenes with Convolutional Sparse Coding and Resonator Networks

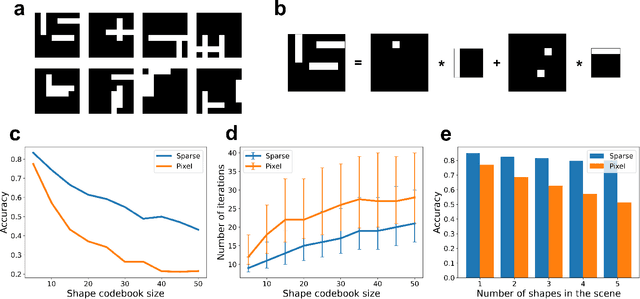
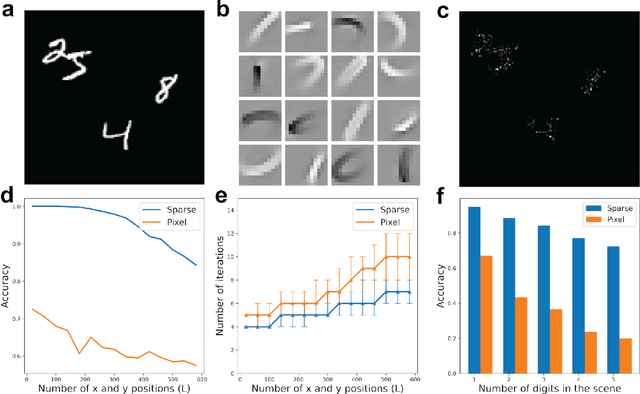
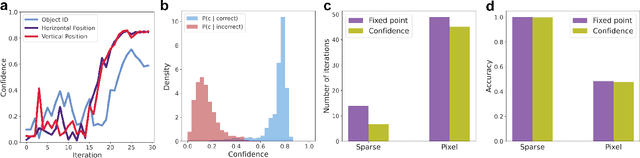
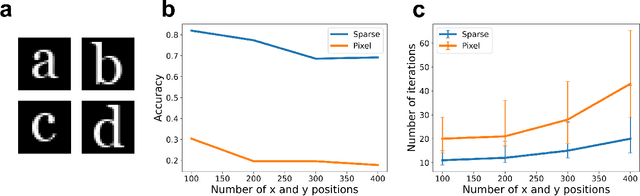
We propose a system for visual scene analysis and recognition based on encoding the sparse, latent feature-representation of an image into a high-dimensional vector that is subsequently factorized to parse scene content. The sparse feature representation is learned from image statistics via convolutional sparse coding, while scene parsing is performed by a resonator network. The integration of sparse coding with the resonator network increases the capacity of distributed representations and reduces collisions in the combinatorial search space during factorization. We find that for this problem the resonator network is capable of fast and accurate vector factorization, and we develop a confidence-based metric that assists in tracking the convergence of the resonator network.

Computing with Residue Numbers in High-Dimensional Representation

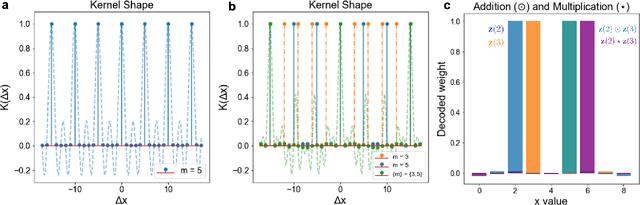
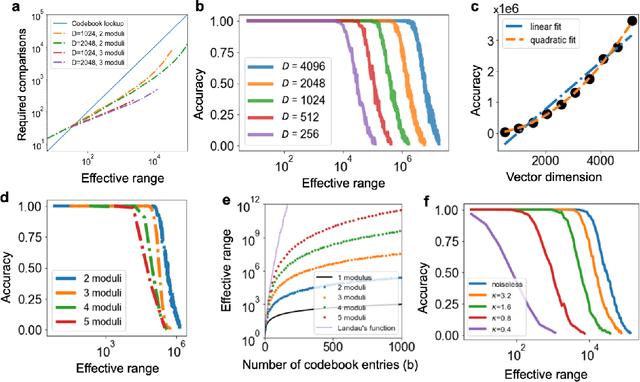
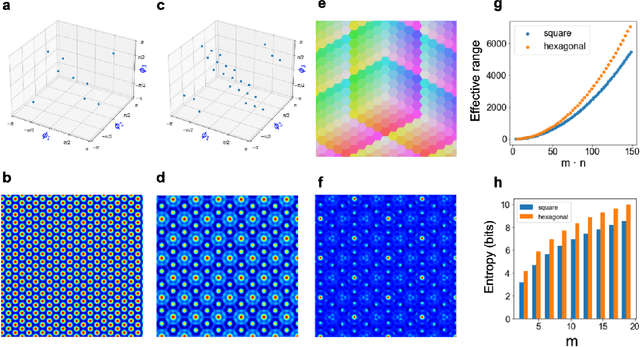
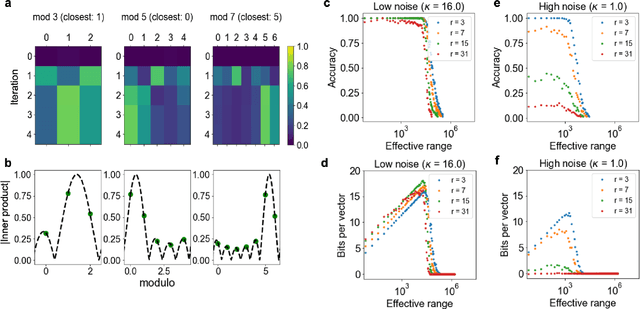
We introduce Residue Hyperdimensional Computing, a computing framework that unifies residue number systems with an algebra defined over random, high-dimensional vectors. We show how residue numbers can be represented as high-dimensional vectors in a manner that allows algebraic operations to be performed with component-wise, parallelizable operations on the vector elements. The resulting framework, when combined with an efficient method for factorizing high-dimensional vectors, can represent and operate on numerical values over a large dynamic range using vastly fewer resources than previous methods, and it exhibits impressive robustness to noise. We demonstrate the potential for this framework to solve computationally difficult problems in visual perception and combinatorial optimization, showing improvement over baseline methods. More broadly, the framework provides a possible account for the computational operations of grid cells in the brain, and it suggests new machine learning architectures for representing and manipulating numerical data.

Efficient Decoding of Compositional Structure in Holistic Representations

We investigate the task of retrieving information from compositional distributed representations formed by Hyperdimensional Computing/Vector Symbolic Architectures and present novel techniques which achieve new information rate bounds. First, we provide an overview of the decoding techniques that can be used to approach the retrieval task. The techniques are categorized into four groups. We then evaluate the considered techniques in several settings that involve, e.g., inclusion of external noise and storage elements with reduced precision. In particular, we find that the decoding techniques from the sparse coding and compressed sensing literature (rarely used for Hyperdimensional Computing/Vector Symbolic Architectures) are also well-suited for decoding information from the compositional distributed representations. Combining these decoding techniques with interference cancellation ideas from communications improves previously reported bounds (Hersche et al., 2021) of the information rate of the distributed representations from 1.20 to 1.40 bits per dimension for smaller codebooks and from 0.60 to 1.26 bits per dimension for larger codebooks.

Efficient Optimization with Higher-Order Ising Machines

A prominent approach to solving combinatorial optimization problems on parallel hardware is Ising machines, i.e., hardware implementations of networks of interacting binary spin variables. Most Ising machines leverage second-order interactions although important classes of optimization problems, such as satisfiability problems, map more seamlessly to Ising networks with higher-order interactions. Here, we demonstrate that higher-order Ising machines can solve satisfiability problems more resource-efficiently in terms of the number of spin variables and their connections when compared to traditional second-order Ising machines. Further, our results show on a benchmark dataset of Boolean \textit{k}-satisfiability problems that higher-order Ising machines implemented with coupled oscillators rapidly find solutions that are better than second-order Ising machines, thus, improving the current state-of-the-art for Ising machines.

Computing with Hypervectors for Efficient Speaker Identification

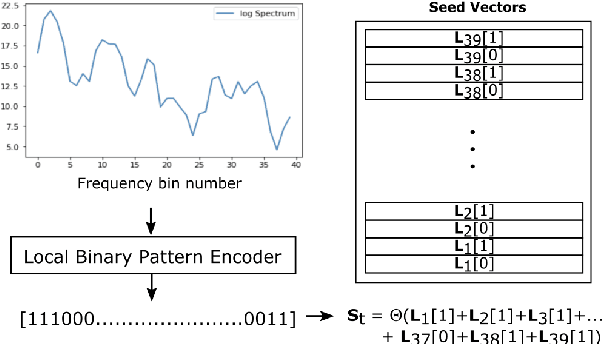
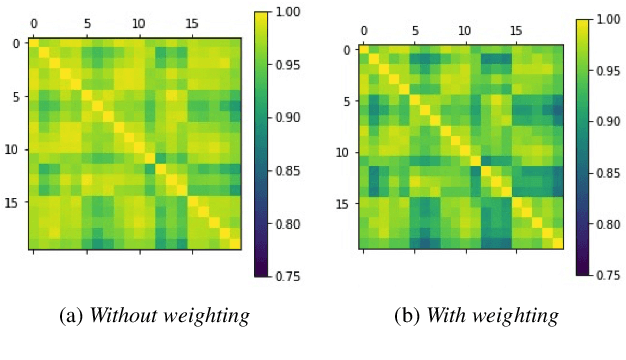
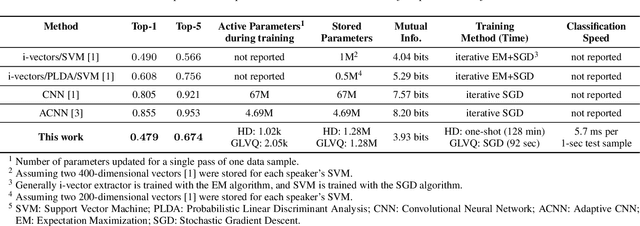
We introduce a method to identify speakers by computing with high-dimensional random vectors. Its strengths are simplicity and speed. With only 1.02k active parameters and a 128-minute pass through the training data we achieve Top-1 and Top-5 scores of 31% and 52% on the VoxCeleb1 dataset of 1,251 speakers. This is in contrast to CNN models requiring several million parameters and orders of magnitude higher computational complexity for only a 2$\times$ gain in discriminative power as measured in mutual information. An additional 92 seconds of training with Generalized Learning Vector Quantization (GLVQ) raises the scores to 48% and 67%. A trained classifier classifies 1 second of speech in 5.7 ms. All processing was done on standard CPU-based machines.

Beyond the Imitation Game: Quantifying and extrapolating the capabilities of language models

Language models demonstrate both quantitative improvement and new qualitative capabilities with increasing scale. Despite their potentially transformative impact, these new capabilities are as yet poorly characterized. In order to inform future research, prepare for disruptive new model capabilities, and ameliorate socially harmful effects, it is vital that we understand the present and near-future capabilities and limitations of language models. To address this challenge, we introduce the Beyond the Imitation Game benchmark (BIG-bench). BIG-bench currently consists of 204 tasks, contributed by 442 authors across 132 institutions. Task topics are diverse, drawing problems from linguistics, childhood development, math, common-sense reasoning, biology, physics, social bias, software development, and beyond. BIG-bench focuses on tasks that are believed to be beyond the capabilities of current language models. We evaluate the behavior of OpenAI's GPT models, Google-internal dense transformer architectures, and Switch-style sparse transformers on BIG-bench, across model sizes spanning millions to hundreds of billions of parameters. In addition, a team of human expert raters performed all tasks in order to provide a strong baseline. Findings include: model performance and calibration both improve with scale, but are poor in absolute terms (and when compared with rater performance); performance is remarkably similar across model classes, though with benefits from sparsity; tasks that improve gradually and predictably commonly involve a large knowledge or memorization component, whereas tasks that exhibit "breakthrough" behavior at a critical scale often involve multiple steps or components, or brittle metrics; social bias typically increases with scale in settings with ambiguous context, but this can be improved with prompting.

Generalized Key-Value Memory to Flexibly Adjust Redundancy in Memory-Augmented Networks

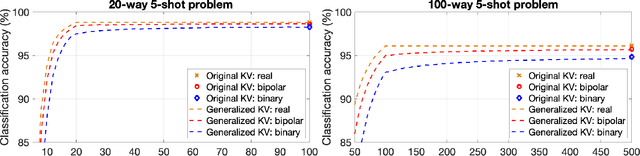
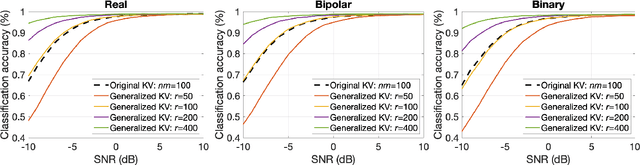
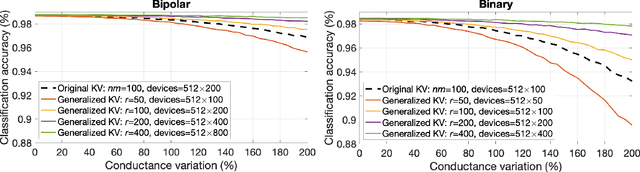
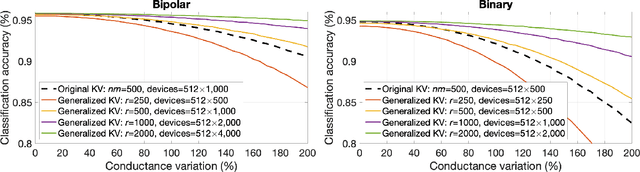
Memory-augmented neural networks enhance a neural network with an external key-value memory whose complexity is typically dominated by the number of support vectors in the key memory. We propose a generalized key-value memory that decouples its dimension from the number of support vectors by introducing a free parameter that can arbitrarily add or remove redundancy to the key memory representation. In effect, it provides an additional degree of freedom to flexibly control the trade-off between robustness and the resources required to store and compute the generalized key-value memory. This is particularly useful for realizing the key memory on in-memory computing hardware where it exploits nonideal, but extremely efficient non-volatile memory devices for dense storage and computation. Experimental results show that adapting this parameter on demand effectively mitigates up to 44% nonidealities, at equal accuracy and number of devices, without any need for neural network retraining.