Recursive Binding for Similarity-Preserving Hypervector Representations of Sequences

Hyperdimensional computing (HDC), also known as vector symbolic architectures (VSA), is a computing framework used within artificial intelligence and cognitive computing that operates with distributed vector representations of large fixed dimensionality. A critical step for designing the HDC/VSA solutions is to obtain such representations from the input data. Here, we focus on sequences and propose their transformation to distributed representations that both preserve the similarity of identical sequence elements at nearby positions and are equivariant to the sequence shift. These properties are enabled by forming representations of sequence positions using recursive binding and superposition operations. The proposed transformation was experimentally investigated with symbolic strings used for modeling human perception of word similarity. The obtained results are on a par with more sophisticated approaches from the literature. The proposed transformation was designed for the HDC/VSA model known as Fourier Holographic Reduced Representations. However, it can be adapted to some other HDC/VSA models.

Shift-Equivariant Similarity-Preserving Hypervector Representations of Sequences

Hyperdimensional Computing (HDC), also known as Vector-Symbolic Architectures (VSA), is a promising framework for the development of cognitive architectures and artificial intelligence systems, as well as for technical applications and emerging neuromorphic and nanoscale hardware. HDC/VSA operate with hypervectors, i.e., distributed vector representations of large fixed dimension (usually > 1000). One of the key ingredients of HDC/VSA are the methods for encoding data of various types (from numeric scalars and vectors to graphs) into hypervectors. In this paper, we propose an approach for the formation of hypervectors of sequences that provides both an equivariance with respect to the shift of sequences and preserves the similarity of sequences with identical elements at nearby positions. Our methods represent the sequence elements by compositional hypervectors and exploit permutations of hypervectors for representing the order of sequence elements. We experimentally explored the proposed representations using a diverse set of tasks with data in the form of symbolic strings. Although our approach is feature-free as it forms the hypervector of a sequence from the hypervectors of its symbols at their positions, it demonstrated the performance on a par with the methods that apply various features, such as subsequences. The proposed techniques were designed for the HDC/VSA model known as Sparse Binary Distributed Representations. However, they can be adapted to hypervectors in formats of other HDC/VSA models, as well as for representing sequences of types other than symbolic strings.

A Survey on Hyperdimensional Computing aka Vector Symbolic Architectures, Part I: Models and Data Transformations

This two-part comprehensive survey is devoted to a computing framework most commonly known under the names Hyperdimensional Computing and Vector Symbolic Architectures (HDC/VSA). Both names refer to a family of computational models that use high-dimensional distributed representations and rely on the algebraic properties of their key operations to incorporate the advantages of structured symbolic representations and vector distributed representations. Notable models in the HDC/VSA family are Tensor Product Representations, Holographic Reduced Representations, Multiply-Add-Permute, Binary Spatter Codes, and Sparse Binary Distributed Representations but there are other models too. HDC/VSA is a highly interdisciplinary area with connections to computer science, electrical engineering, artificial intelligence, mathematics, and cognitive science. This fact makes it challenging to create a thorough overview of the area. However, due to a surge of new researchers joining the area in recent years, the necessity for a comprehensive survey of the area has become extremely important. Therefore, amongst other aspects of the area, this Part I surveys important aspects such as: known computational models of HDC/VSA and transformations of various input data types to high-dimensional distributed representations. Part II of this survey is devoted to applications, cognitive computing and architectures, as well as directions for future work. The survey is written to be useful for both newcomers and practitioners.

Vector Symbolic Architectures as a Computing Framework for Nanoscale Hardware

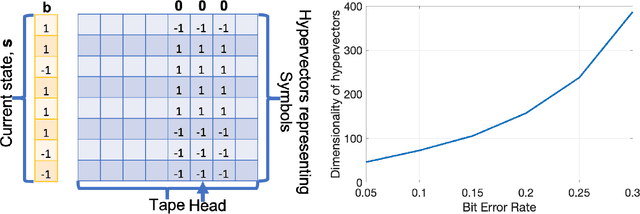
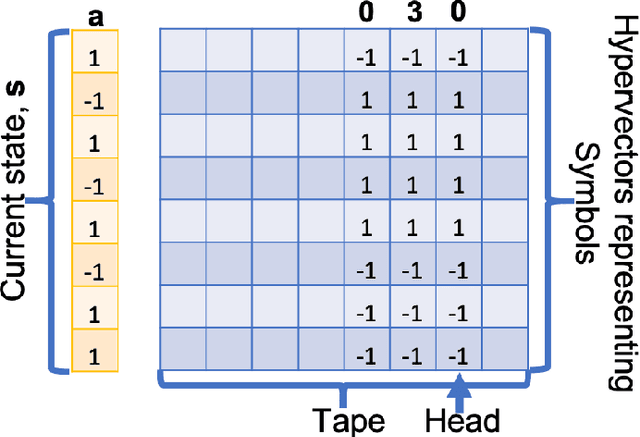
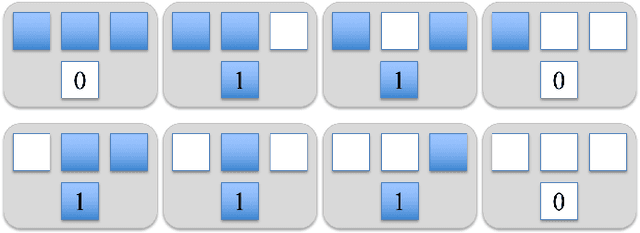
This article reviews recent progress in the development of the computing framework Vector Symbolic Architectures (also known as Hyperdimensional Computing). This framework is well suited for implementation in stochastic, nanoscale hardware and it naturally expresses the types of cognitive operations required for Artificial Intelligence (AI). We demonstrate in this article that the ring-like algebraic structure of Vector Symbolic Architectures offers simple but powerful operations on high-dimensional vectors that can support all data structures and manipulations relevant in modern computing. In addition, we illustrate the distinguishing feature of Vector Symbolic Architectures, "computing in superposition," which sets it apart from conventional computing. This latter property opens the door to efficient solutions to the difficult combinatorial search problems inherent in AI applications. Vector Symbolic Architectures are Turing complete, as we show, and we see them acting as a framework for computing with distributed representations in myriad AI settings. This paper serves as a reference for computer architects by illustrating techniques and philosophy of VSAs for distributed computing and relevance to emerging computing hardware, such as neuromorphic computing.