Vector Symbolic Architectures as a Computing Framework for Nanoscale Hardware

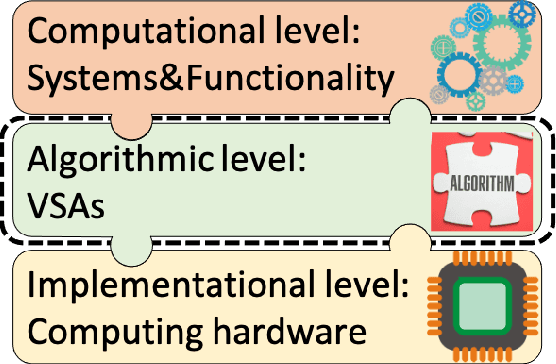
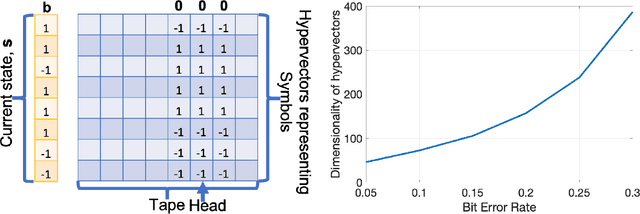
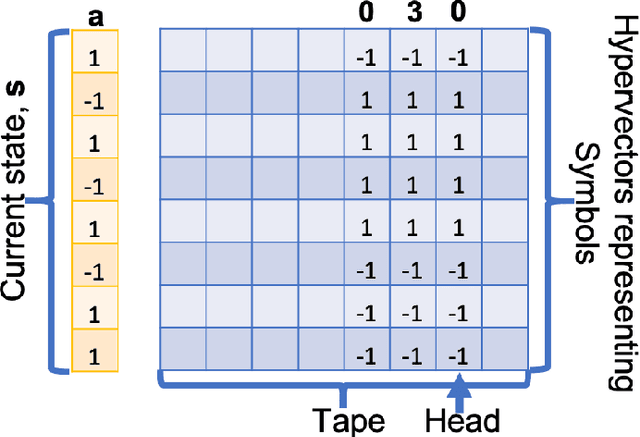
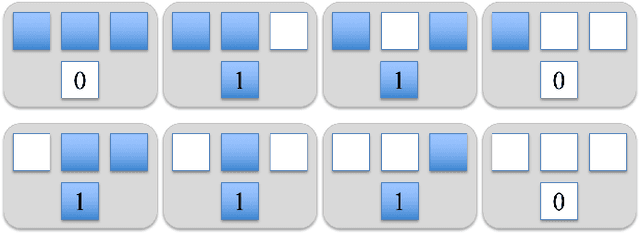
This article reviews recent progress in the development of the computing framework Vector Symbolic Architectures (also known as Hyperdimensional Computing). This framework is well suited for implementation in stochastic, nanoscale hardware and it naturally expresses the types of cognitive operations required for Artificial Intelligence (AI). We demonstrate in this article that the ring-like algebraic structure of Vector Symbolic Architectures offers simple but powerful operations on high-dimensional vectors that can support all data structures and manipulations relevant in modern computing. In addition, we illustrate the distinguishing feature of Vector Symbolic Architectures, "computing in superposition," which sets it apart from conventional computing. This latter property opens the door to efficient solutions to the difficult combinatorial search problems inherent in AI applications. Vector Symbolic Architectures are Turing complete, as we show, and we see them acting as a framework for computing with distributed representations in myriad AI settings. This paper serves as a reference for computer architects by illustrating techniques and philosophy of VSAs for distributed computing and relevance to emerging computing hardware, such as neuromorphic computing.

Resonator Circuits for factoring high-dimensional vectors

We describe a type of neural network, called a Resonator Circuit, that factors high-dimensional vectors. Given a composite vector formed by the Hadamard product of several other vectors drawn from a discrete set, a Resonator Circuit can efficiently decompose the composite into these factors. This paper focuses on the case of "bipolar" vectors whose elements are $\pm1$ and characterizes the solution quality, stability properties, and speed of Resonator Circuits in comparison to several benchmark optimization methods including Alternating Least Squares, Iterative Soft Thresholding, and Multiplicative Weights. We find that Resonator Circuits substantially outperform these alternative methods by leveraging a combination of powerful nonlinear dynamics and "searching in superposition", by which we mean that estimates of the correct solution are, at any given time, formed from a weighted superposition of all possible solutions. The considered alternative methods also search in superposition, but the dynamics of Resonator Circuits allow them to strike a more natural balance between exploring the solution space and exploiting local information to drive the network toward probable solutions. Resonator Circuits can be conceptualized as a set of interconnected Hopfield Networks, and this leads to some interesting analysis. In particular, while a Hopfield Network descends an energy function and is guaranteed to converge, a Resonator Circuit is not. However, there exists a high-fidelity regime where Resonator Circuits almost always do converge, and they can solve the factorization problem extremely well. As factorization is central to many aspects of perception and cognition, we believe that Resonator Circuits may bring us a step closer to understanding how this computationally difficult problem is efficiently solved by neural circuits in brains.