Computing with Residue Numbers in High-Dimensional Representation

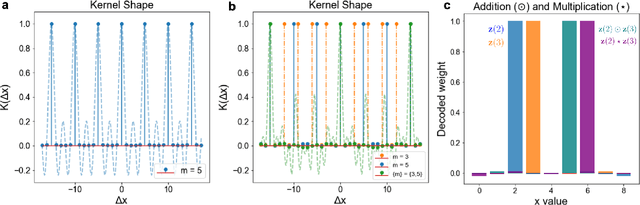
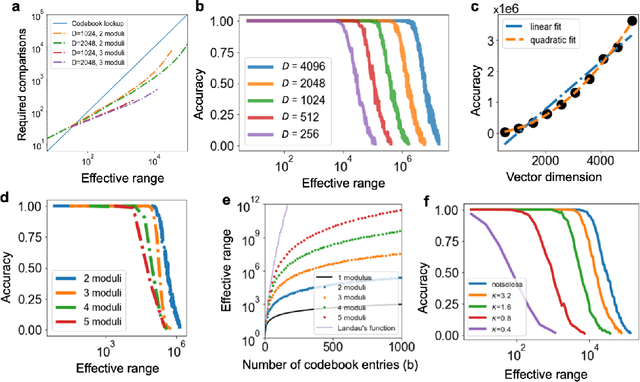
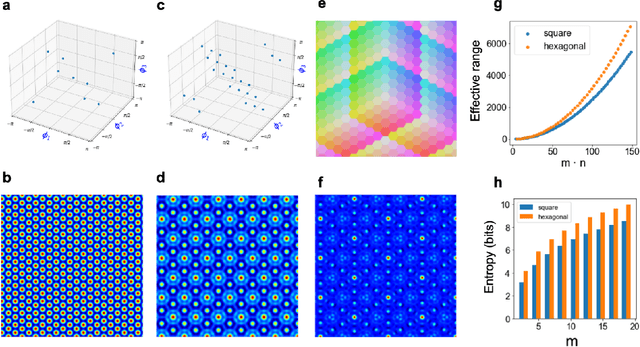
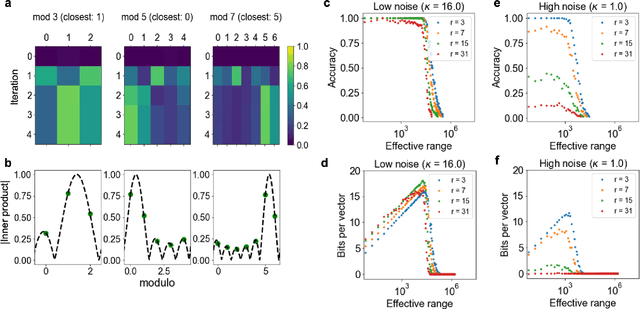
We introduce Residue Hyperdimensional Computing, a computing framework that unifies residue number systems with an algebra defined over random, high-dimensional vectors. We show how residue numbers can be represented as high-dimensional vectors in a manner that allows algebraic operations to be performed with component-wise, parallelizable operations on the vector elements. The resulting framework, when combined with an efficient method for factorizing high-dimensional vectors, can represent and operate on numerical values over a large dynamic range using vastly fewer resources than previous methods, and it exhibits impressive robustness to noise. We demonstrate the potential for this framework to solve computationally difficult problems in visual perception and combinatorial optimization, showing improvement over baseline methods. More broadly, the framework provides a possible account for the computational operations of grid cells in the brain, and it suggests new machine learning architectures for representing and manipulating numerical data.

Efficient Decoding of Compositional Structure in Holistic Representations

We investigate the task of retrieving information from compositional distributed representations formed by Hyperdimensional Computing/Vector Symbolic Architectures and present novel techniques which achieve new information rate bounds. First, we provide an overview of the decoding techniques that can be used to approach the retrieval task. The techniques are categorized into four groups. We then evaluate the considered techniques in several settings that involve, e.g., inclusion of external noise and storage elements with reduced precision. In particular, we find that the decoding techniques from the sparse coding and compressed sensing literature (rarely used for Hyperdimensional Computing/Vector Symbolic Architectures) are also well-suited for decoding information from the compositional distributed representations. Combining these decoding techniques with interference cancellation ideas from communications improves previously reported bounds (Hersche et al., 2021) of the information rate of the distributed representations from 1.20 to 1.40 bits per dimension for smaller codebooks and from 0.60 to 1.26 bits per dimension for larger codebooks.

Efficient Optimization with Higher-Order Ising Machines

A prominent approach to solving combinatorial optimization problems on parallel hardware is Ising machines, i.e., hardware implementations of networks of interacting binary spin variables. Most Ising machines leverage second-order interactions although important classes of optimization problems, such as satisfiability problems, map more seamlessly to Ising networks with higher-order interactions. Here, we demonstrate that higher-order Ising machines can solve satisfiability problems more resource-efficiently in terms of the number of spin variables and their connections when compared to traditional second-order Ising machines. Further, our results show on a benchmark dataset of Boolean \textit{k}-satisfiability problems that higher-order Ising machines implemented with coupled oscillators rapidly find solutions that are better than second-order Ising machines, thus, improving the current state-of-the-art for Ising machines.

Cross-Frequency Coupling Increases Memory Capacity in Oscillatory Neural Networks

An open problem in neuroscience is to explain the functional role of oscillations in neural networks, contributing, for example, to perception, attention, and memory. Cross-frequency coupling (CFC) is associated with information integration across populations of neurons. Impaired CFC is linked to neurological disease. It is unclear what role CFC has in information processing and brain functional connectivity. We construct a model of CFC which predicts a computational role for observed $\theta - \gamma$ oscillatory circuits in the hippocampus and cortex. Our model predicts that the complex dynamics in recurrent and feedforward networks of coupled oscillators performs robust information storage and pattern retrieval. Based on phasor associative memories (PAM), we present a novel oscillator neural network (ONN) model that includes subharmonic injection locking (SHIL) and which reproduces experimental observations of CFC. We show that the presence of CFC increases the memory capacity of a population of neurons connected by plastic synapses. CFC enables error-free pattern retrieval whereas pattern retrieval fails without CFC. In addition, the trade-offs between sparse connectivity, capacity, and information per connection are identified. The associative memory is based on a complex-valued neural network, or phasor neural network (PNN). We show that for values of $Q$ which are the same as the ratio of $\gamma$ to $\theta$ oscillations observed in the hippocampus and the cortex, the associative memory achieves greater capacity and information storage than previous models. The novel contributions of this work are providing a computational framework based on oscillator dynamics which predicts the functional role of neural oscillations and connecting concepts in neural network theory and dynamical system theory.

Deep Learning in Spiking Phasor Neural Networks

Spiking Neural Networks (SNNs) have attracted the attention of the deep learning community for use in low-latency, low-power neuromorphic hardware, as well as models for understanding neuroscience. In this paper, we introduce Spiking Phasor Neural Networks (SPNNs). SPNNs are based on complex-valued Deep Neural Networks (DNNs), representing phases by spike times. Our model computes robustly employing a spike timing code and gradients can be formed using the complex domain. We train SPNNs on CIFAR-10, and demonstrate that the performance exceeds that of other timing coded SNNs, approaching results with comparable real-valued DNNs.

Integer Factorization with Compositional Distributed Representations

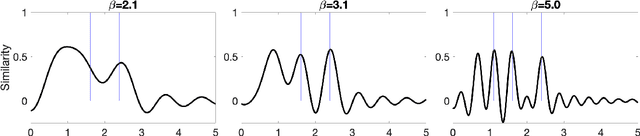
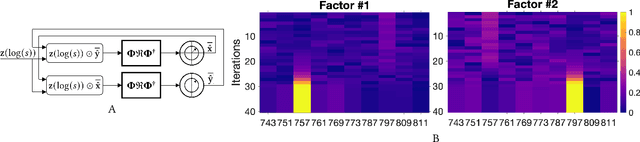
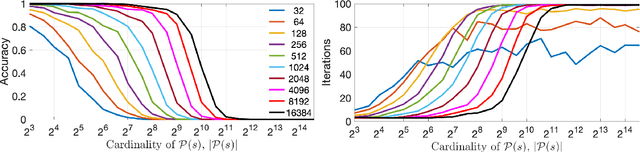
In this paper, we present an approach to integer factorization using distributed representations formed with Vector Symbolic Architectures. The approach formulates integer factorization in a manner such that it can be solved using neural networks and potentially implemented on parallel neuromorphic hardware. We introduce a method for encoding numbers in distributed vector spaces and explain how the resonator network can solve the integer factorization problem. We evaluate the approach on factorization of semiprimes by measuring the factorization accuracy versus the scale of the problem. We also demonstrate how the proposed approach generalizes beyond the factorization of semiprimes; in principle, it can be used for factorization of any composite number. This work demonstrates how a well-known combinatorial search problem may be formulated and solved within the framework of Vector Symbolic Architectures, and it opens the door to solving similarly difficult problems in other domains.