Resonator networks for factoring distributed representations of data structures
Paper and Code
Jul 07, 2020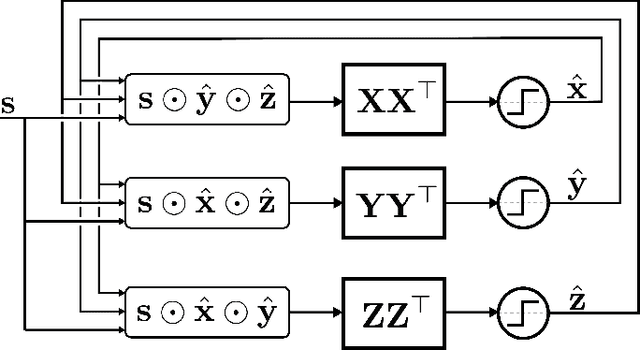
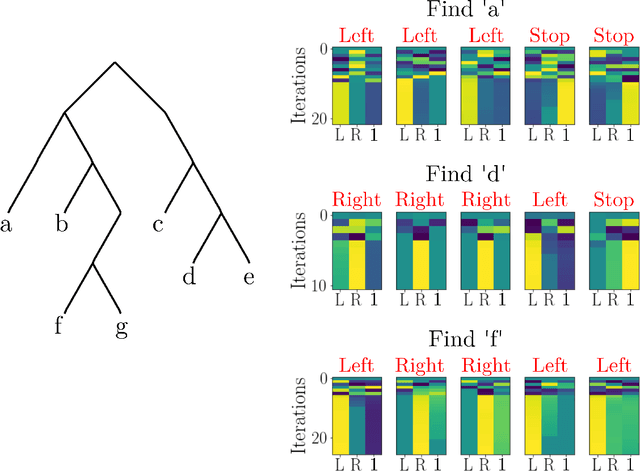
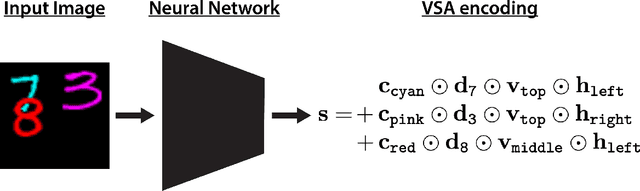
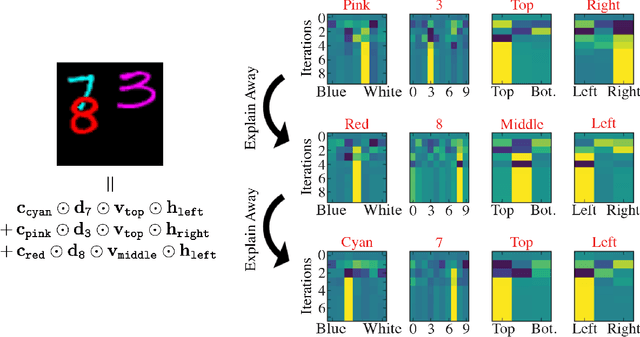
The ability to encode and manipulate data structures with distributed neural representations could qualitatively enhance the capabilities of traditional neural networks by supporting rule-based symbolic reasoning, a central property of cognition. Here we show how this may be accomplished within the framework of Vector Symbolic Architectures (VSA) (Plate, 1991; Gayler, 1998; Kanerva, 1996), whereby data structures are encoded by combining high-dimensional vectors with operations that together form an algebra on the space of distributed representations. In particular, we propose an efficient solution to a hard combinatorial search problem that arises when decoding elements of a VSA data structure: the factorization of products of multiple code vectors. Our proposed algorithm, called a resonator network, is a new type of recurrent neural network that interleaves VSA multiplication operations and pattern completion. We show in two examples -- parsing of a tree-like data structure and parsing of a visual scene -- how the factorization problem arises and how the resonator network can solve it. More broadly, resonator networks open the possibility to apply VSAs to myriad artificial intelligence problems in real-world domains. A companion paper (Kent et al., 2020) presents a rigorous analysis and evaluation of the performance of resonator networks, showing it out-performs alternative approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge