Learning and Inference in Sparse Coding Models with Langevin Dynamics

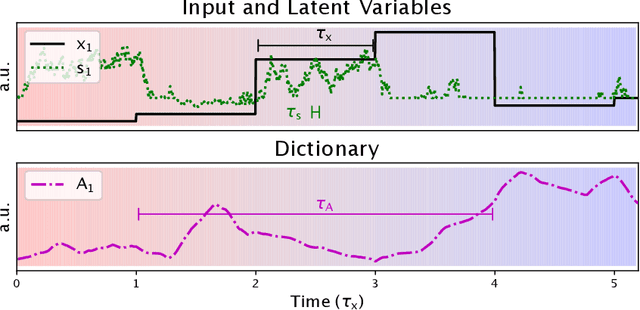
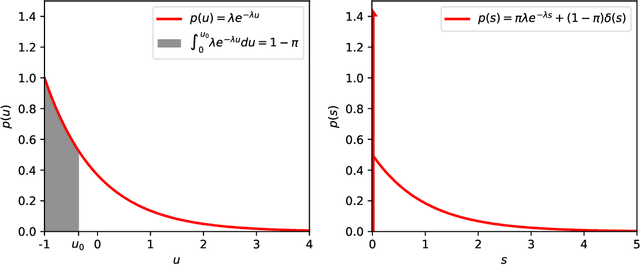
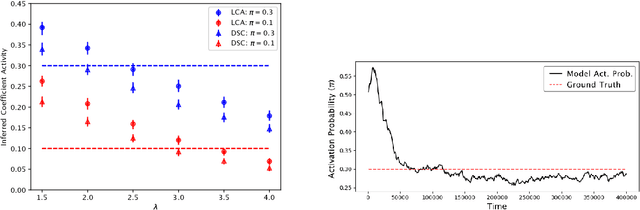
We describe a stochastic, dynamical system capable of inference and learning in a probabilistic latent variable model. The most challenging problem in such models - sampling the posterior distribution over latent variables - is proposed to be solved by harnessing natural sources of stochasticity inherent in electronic and neural systems. We demonstrate this idea for a sparse coding model by deriving a continuous-time equation for inferring its latent variables via Langevin dynamics. The model parameters are learned by simultaneously evolving according to another continuous-time equation, thus bypassing the need for digital accumulators or a global clock. Moreover we show that Langevin dynamics lead to an efficient procedure for sampling from the posterior distribution in the 'L0 sparse' regime, where latent variables are encouraged to be set to zero as opposed to having a small L1 norm. This allows the model to properly incorporate the notion of sparsity rather than having to resort to a relaxed version of sparsity to make optimization tractable. Simulations of the proposed dynamical system on both synthetic and natural image datasets demonstrate that the model is capable of probabilistically correct inference, enabling learning of the dictionary as well as parameters of the prior.

Design of optical neural networks with component imprecisions

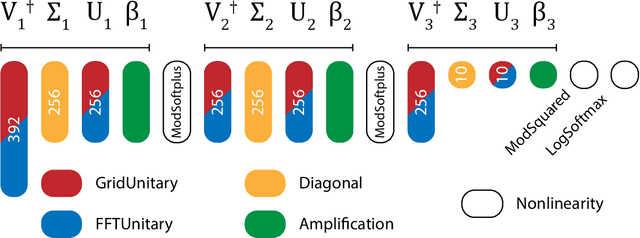
For the benefit of designing scalable, fault resistant optical neural networks (ONNs), we investigate the effects architectural designs have on the ONNs' robustness to imprecise components. We train two ONNs -- one with a more tunable design (GridNet) and one with better fault tolerance (FFTNet) -- to classify handwritten digits. When simulated without any imperfections, GridNet yields a better accuracy (~98%) than FFTNet (~95%). However, under a small amount of error in their photonic components, the more fault tolerant FFTNet overtakes GridNet. We further provide thorough quantitative and qualitative analyses of ONNs' sensitivity to varying levels and types of imprecisions. Our results offer guidelines for the principled design of fault-tolerant ONNs as well as a foundation for further research.

3DQ: Compact Quantized Neural Networks for Volumetric Whole Brain Segmentation

Model architectures have been dramatically increasing in size, improving performance at the cost of resource requirements. In this paper we propose 3DQ, a ternary quantization method, applied for the first time to 3D Fully Convolutional Neural Networks (F-CNNs), enabling 16x model compression while maintaining performance on par with full precision models. We extensively evaluate 3DQ on two datasets for the challenging task of whole brain segmentation. Additionally, we showcase our method's ability to generalize on two common 3D architectures, namely 3D U-Net and V-Net. Outperforming a variety of baselines, the proposed method is capable of compressing large 3D models to a few MBytes, alleviating the storage needs in space critical applications.