Casimir Wierzynski
Learning Irreducible Representations of Noncommutative Lie Groups
Jun 01, 2020



Abstract:Recent work has made exciting theoretical and practical progress towards neural networks that are equivariant to symmetries such as rotations. However, current techniques require explicit group representations, which generally limits us to those groups with analytically derived matrix formulas. In this work, we present a numerical technique for finding irreducible representations of noncommutative Lie groups. We demonstrate that the structure of the Lie algebras associated with these groups can be used to learn explicit representation matrices to high precision. This provides an automated program to build neural networks that are equivariant to a much wider class of transformations, including previously intractable cases such as the Poincar\'e group (rotations, translations, and boosts).
Design of optical neural networks with component imprecisions
Dec 13, 2019
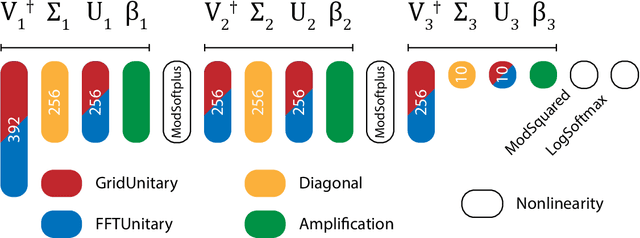


Abstract:For the benefit of designing scalable, fault resistant optical neural networks (ONNs), we investigate the effects architectural designs have on the ONNs' robustness to imprecise components. We train two ONNs -- one with a more tunable design (GridNet) and one with better fault tolerance (FFTNet) -- to classify handwritten digits. When simulated without any imperfections, GridNet yields a better accuracy (~98%) than FFTNet (~95%). However, under a small amount of error in their photonic components, the more fault tolerant FFTNet overtakes GridNet. We further provide thorough quantitative and qualitative analyses of ONNs' sensitivity to varying levels and types of imprecisions. Our results offer guidelines for the principled design of fault-tolerant ONNs as well as a foundation for further research.
Cross-Classification Clustering: An Efficient Multi-Object Tracking Technique for 3-D Instance Segmentation in Connectomics
Dec 04, 2018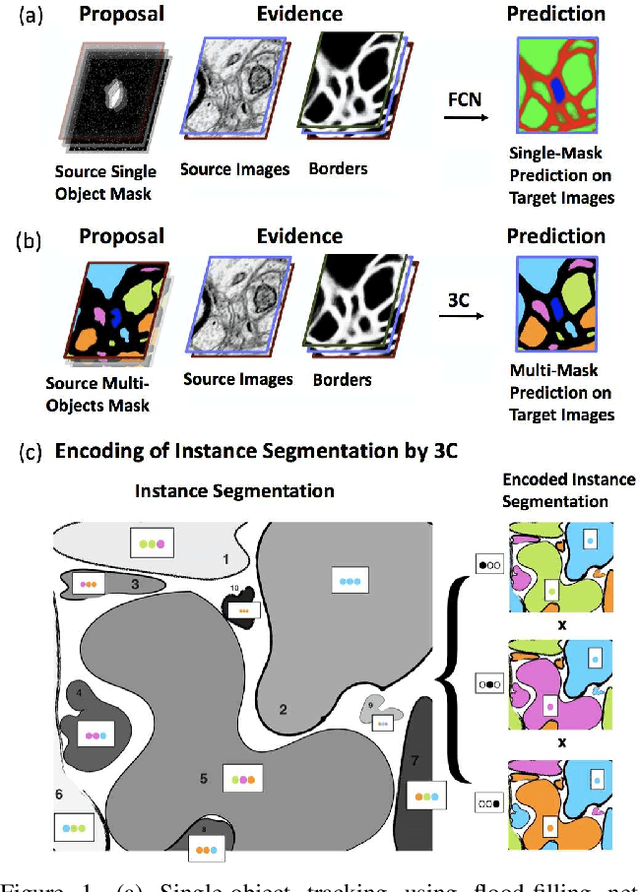
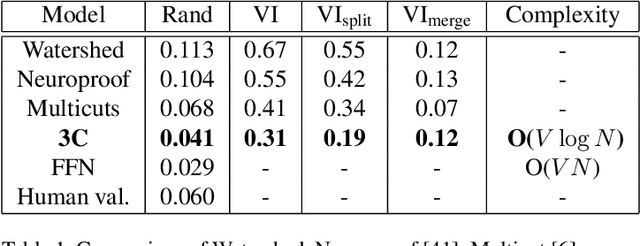
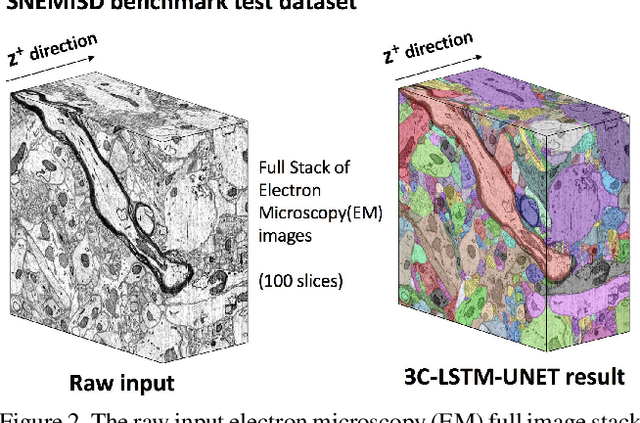
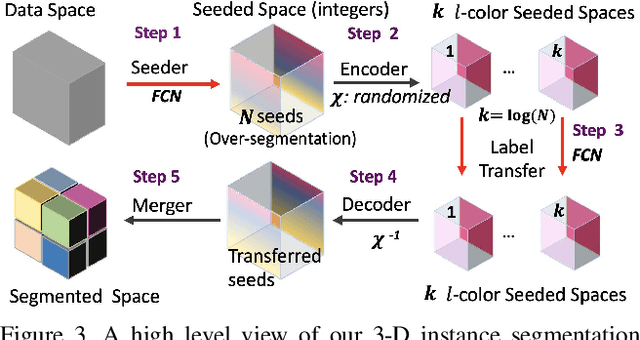
Abstract:Pixel-accurate tracking of objects is a key element in many computer vision applications, often solved by iterated individual object tracking or instance segmentation followed by object matching. Here we introduce cross-classification clustering (3C), a new technique that simultaneously tracks all objects in an image stack. The key idea in cross-classification is to efficiently turn a clustering problem into a classification problem by running a logarithmic number of independent classifications, letting the cross-labeling of these classifications uniquely classify each pixel to the object labels. We apply the 3C mechanism to achieve state-of-the-art accuracy in connectomics - nanoscale mapping of the brain from electron microscopy volumes. Our reconstruction system introduces an order of magnitude scalability improvement over the best current methods for neuronal reconstruction, and can be seamlessly integrated within existing single-object tracking methods like Google's flood-filling networks to improve their performance. This scalability is crucial for the real-world deployment of connectomics pipelines, as the best performing existing techniques require computing infrastructures that are beyond the reach of most labs. We believe 3C has valuable scalability implications in other domains that require pixel-accurate tracking of multiple objects in image stacks or video.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge