Mayur Mudigonda
Learning and Inference in Sparse Coding Models with Langevin Dynamics
Apr 23, 2022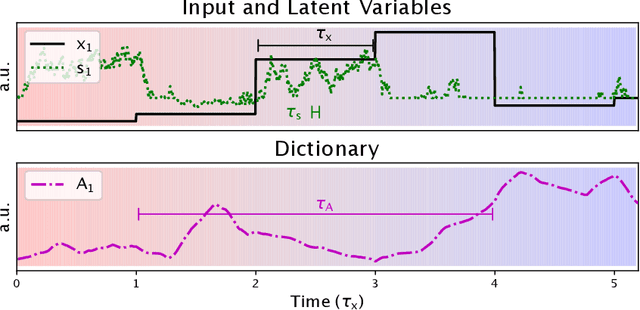
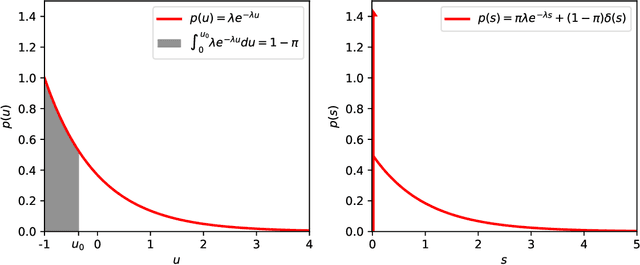

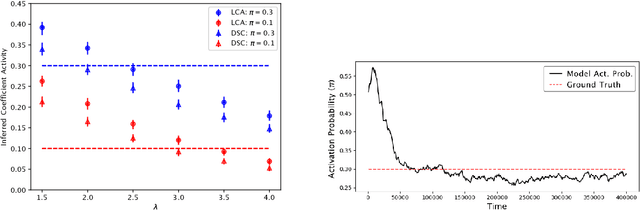
Abstract:We describe a stochastic, dynamical system capable of inference and learning in a probabilistic latent variable model. The most challenging problem in such models - sampling the posterior distribution over latent variables - is proposed to be solved by harnessing natural sources of stochasticity inherent in electronic and neural systems. We demonstrate this idea for a sparse coding model by deriving a continuous-time equation for inferring its latent variables via Langevin dynamics. The model parameters are learned by simultaneously evolving according to another continuous-time equation, thus bypassing the need for digital accumulators or a global clock. Moreover we show that Langevin dynamics lead to an efficient procedure for sampling from the posterior distribution in the 'L0 sparse' regime, where latent variables are encouraged to be set to zero as opposed to having a small L1 norm. This allows the model to properly incorporate the notion of sparsity rather than having to resort to a relaxed version of sparsity to make optimization tractable. Simulations of the proposed dynamical system on both synthetic and natural image datasets demonstrate that the model is capable of probabilistically correct inference, enabling learning of the dictionary as well as parameters of the prior.
Manipulation by Feel: Touch-Based Control with Deep Predictive Models
Mar 11, 2019

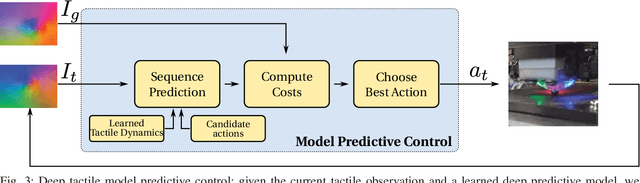
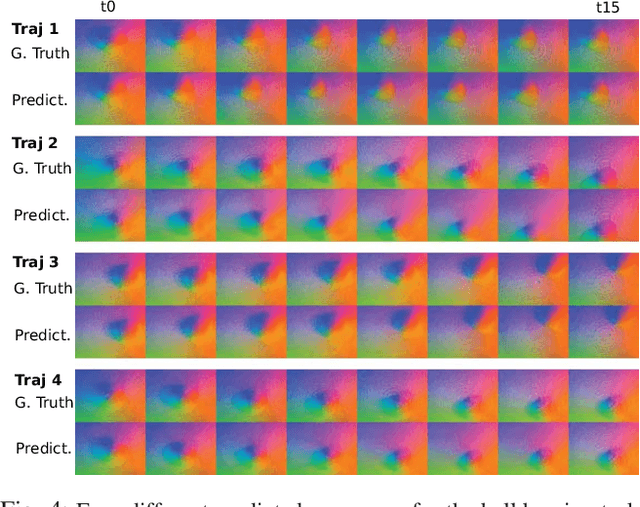
Abstract:Touch sensing is widely acknowledged to be important for dexterous robotic manipulation, but exploiting tactile sensing for continuous, non-prehensile manipulation is challenging. General purpose control techniques that are able to effectively leverage tactile sensing as well as accurate physics models of contacts and forces remain largely elusive, and it is unclear how to even specify a desired behavior in terms of tactile percepts. In this paper, we take a step towards addressing these issues by combining high-resolution tactile sensing with data-driven modeling using deep neural network dynamics models. We propose deep tactile MPC, a framework for learning to perform tactile servoing from raw tactile sensor inputs, without manual supervision. We show that this method enables a robot equipped with a GelSight-style tactile sensor to manipulate a ball, analog stick, and 20-sided die, learning from unsupervised autonomous interaction and then using the learned tactile predictive model to reposition each object to user-specified configurations, indicated by a goal tactile reading. Videos, visualizations and the code are available here: https://sites.google.com/view/deeptactilempc
Hamiltonian Monte Carlo Without Detailed Balance
Mar 25, 2016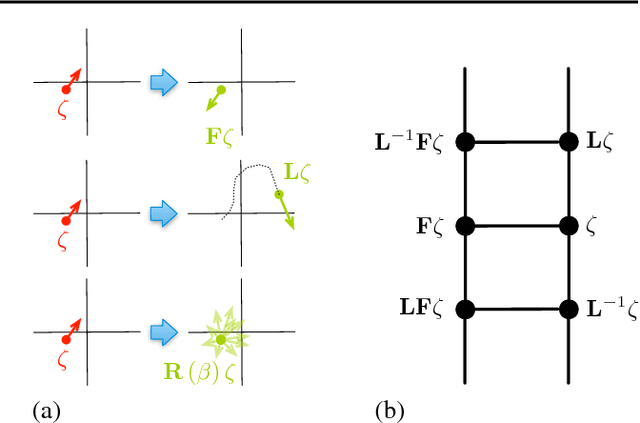
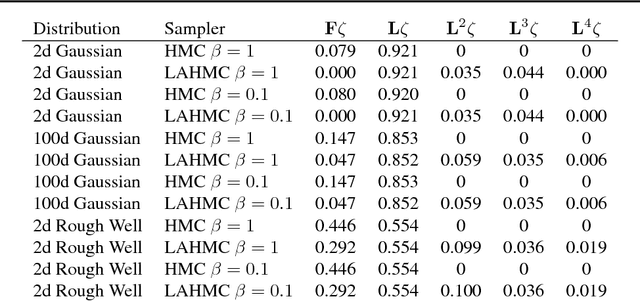
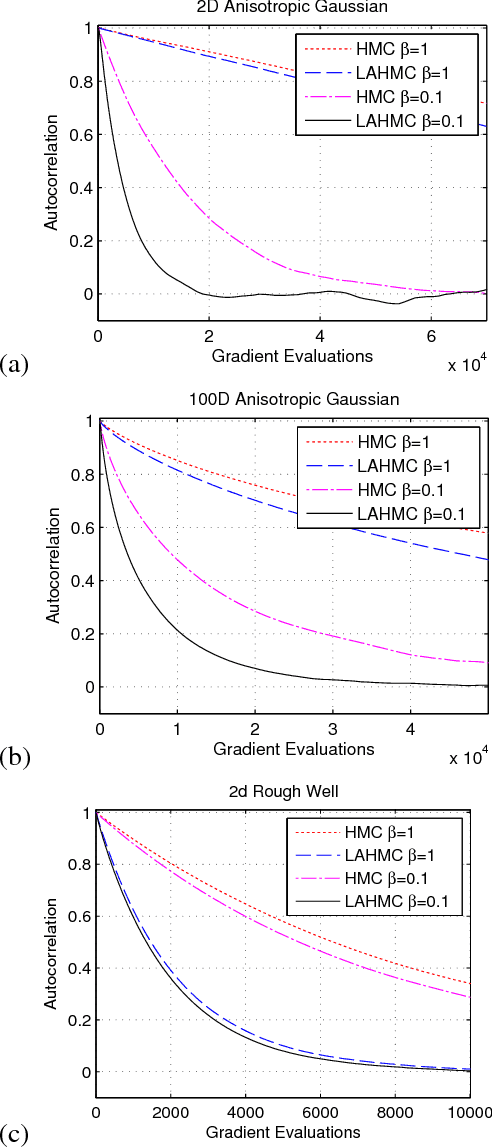
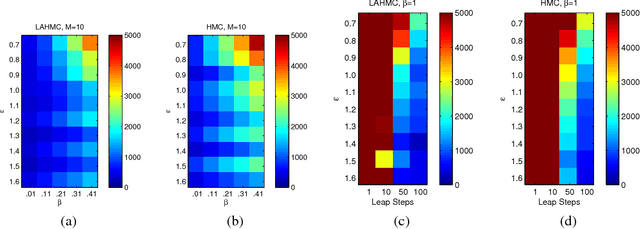
Abstract:We present a method for performing Hamiltonian Monte Carlo that largely eliminates sample rejection for typical hyperparameters. In situations that would normally lead to rejection, instead a longer trajectory is computed until a new state is reached that can be accepted. This is achieved using Markov chain transitions that satisfy the fixed point equation, but do not satisfy detailed balance. The resulting algorithm significantly suppresses the random walk behavior and wasted function evaluations that are typically the consequence of update rejection. We demonstrate a greater than factor of two improvement in mixing time on three test problems. We release the source code as Python and MATLAB packages.
A Markov Jump Process for More Efficient Hamiltonian Monte Carlo
Oct 11, 2015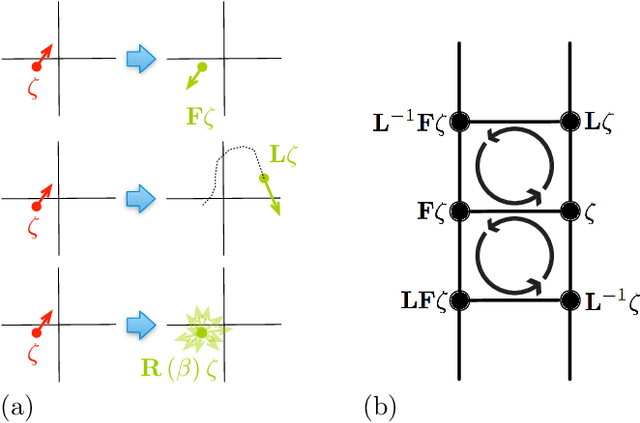



Abstract:In most sampling algorithms, including Hamiltonian Monte Carlo, transition rates between states correspond to the probability of making a transition in a single time step, and are constrained to be less than or equal to 1. We derive a Hamiltonian Monte Carlo algorithm using a continuous time Markov jump process, and are thus able to escape this constraint. Transition rates in a Markov jump process need only be non-negative. We demonstrate that the new algorithm leads to improved mixing for several example problems, both by evaluating the spectral gap of the Markov operator, and by computing autocorrelation as a function of compute time. We release the algorithm as an open source Python package.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge