On Principles of Emergent Organization

After more than a century of concerted effort, physics still lacks basic principles of spontaneous self-organization. To appreciate why, we first state the problem, outline historical approaches, and survey the present state of the physics of self-organization. This frames the particular challenges arising from mathematical intractability and the resulting need for computational approaches, as well as those arising from a chronic failure to define structure. Then, an overview of two modern mathematical formulations of organization -- intrinsic computation and evolution operators -- lays out a way to overcome these challenges. Together, the vantage point they afford shows how to account for the emergence of structured states via a statistical mechanics of systems arbitrarily far from equilibrium. The result is a constructive path forward to principles of organization that builds on mathematical identification of structure.

Physics-Informed Representation Learning for Emergent Organization in Complex Dynamical Systems

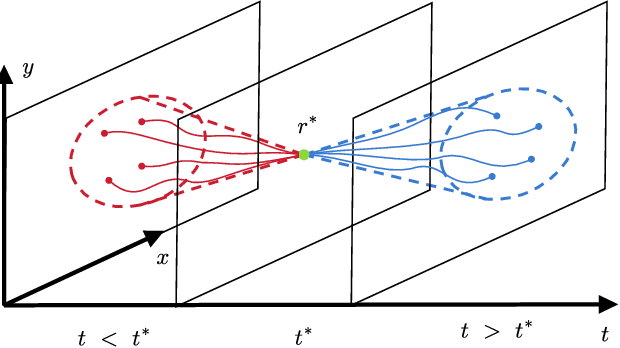
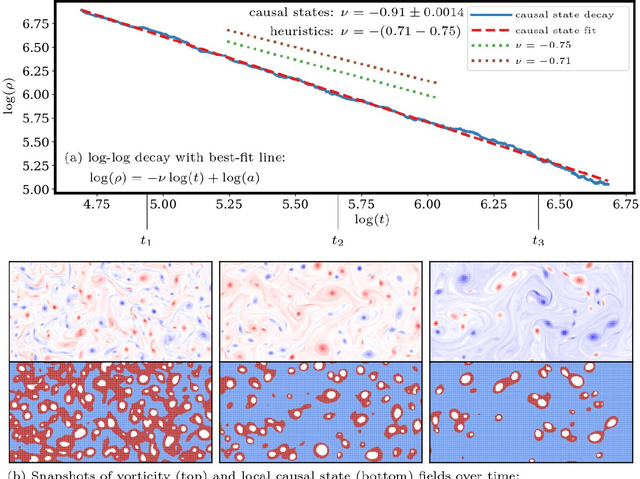
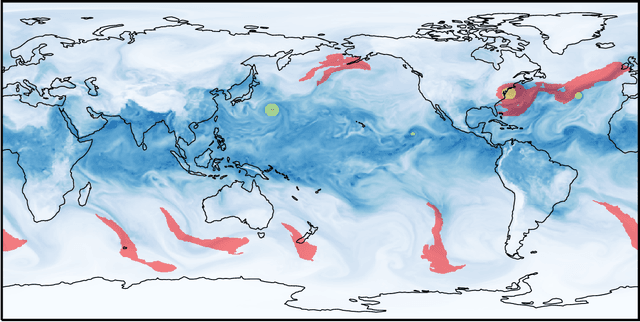
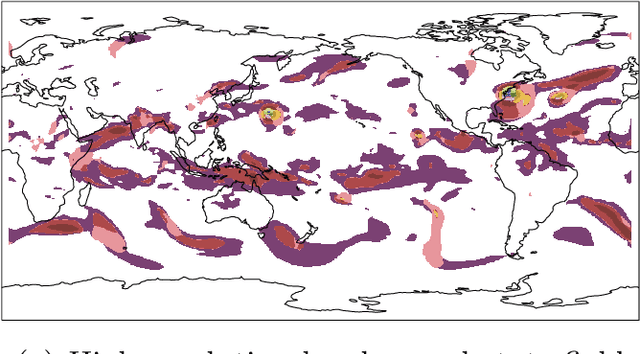
Nonlinearly interacting system components often introduce instabilities that generate phenomena with new properties and at different space-time scales than the components. This is known as spontaneous self-organization and is ubiquitous in systems far from thermodynamic equilibrium. We introduce a theoretically-grounded framework for emergent organization that, via data-driven algorithms, is constructive in practice. Its building blocks are spacetime lightcones that capture how information propagates across a system through local interactions. We show that predictive equivalence classes of lightcones, local causal states, capture organized behaviors and coherent structures in complex spatiotemporal systems. Using our unsupervised physics-informed machine learning algorithm and a high-performance computing implementation, we demonstrate the applicability of the local causal states for real-world domain science problems. We show that the local causal states capture vortices and their power-law decay behavior in two-dimensional turbulence. We then show that known (hurricanes and atmospheric rivers) and novel extreme weather events can be identified on a pixel-level basis and tracked through time in high-resolution climate data.

Complexity-calibrated Benchmarks for Machine Learning Reveal When Next-Generation Reservoir Computer Predictions Succeed and Mislead

Recurrent neural networks are used to forecast time series in finance, climate, language, and from many other domains. Reservoir computers are a particularly easily trainable form of recurrent neural network. Recently, a "next-generation" reservoir computer was introduced in which the memory trace involves only a finite number of previous symbols. We explore the inherent limitations of finite-past memory traces in this intriguing proposal. A lower bound from Fano's inequality shows that, on highly non-Markovian processes generated by large probabilistic state machines, next-generation reservoir computers with reasonably long memory traces have an error probability that is at least ~ 60% higher than the minimal attainable error probability in predicting the next observation. More generally, it appears that popular recurrent neural networks fall far short of optimally predicting such complex processes. These results highlight the need for a new generation of optimized recurrent neural network architectures. Alongside this finding, we present concentration-of-measure results for randomly-generated but complex processes. One conclusion is that large probabilistic state machines -- specifically, large $\epsilon$-machines -- are key to generating challenging and structurally-unbiased stimuli for ground-truthing recurrent neural network architectures.

Exploring Predictive States via Cantor Embeddings and Wasserstein Distance

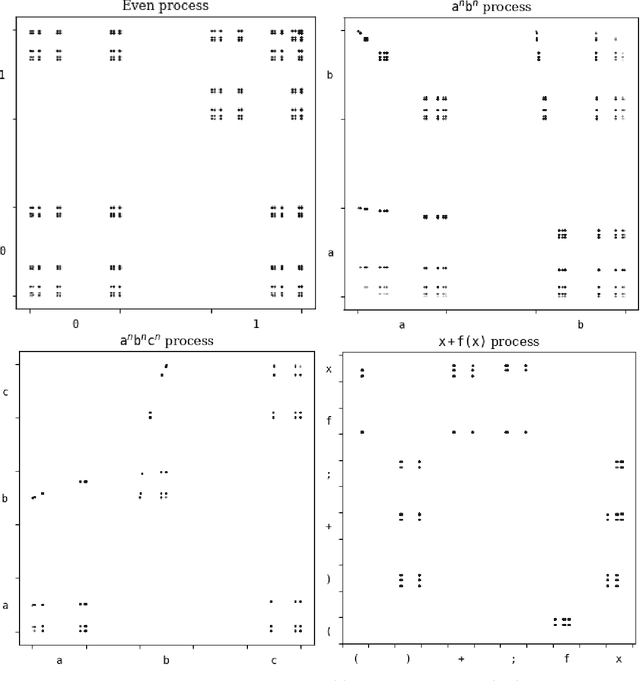
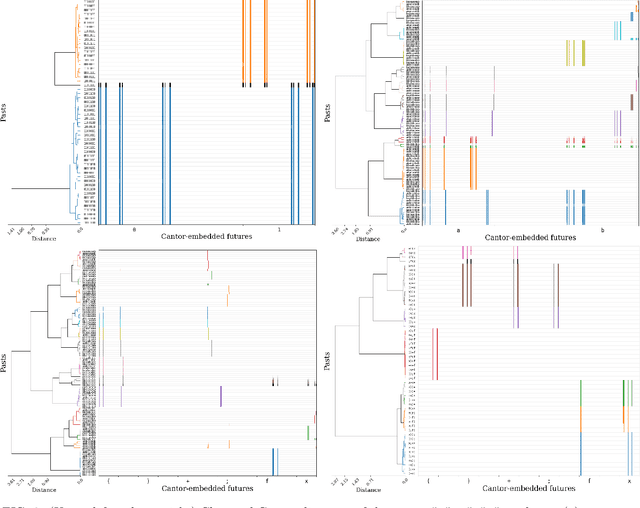
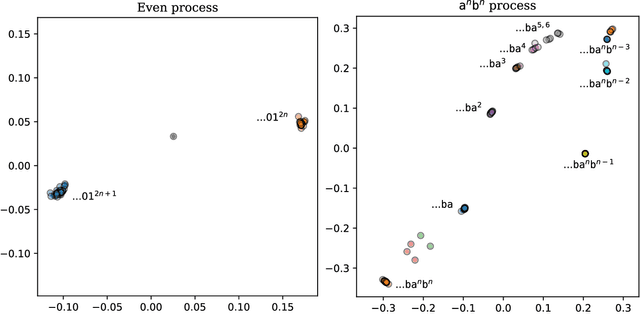
Predictive states for stochastic processes are a nonparametric and interpretable construct with relevance across a multitude of modeling paradigms. Recent progress on the self-supervised reconstruction of predictive states from time-series data focused on the use of reproducing kernel Hilbert spaces. Here, we examine how Wasserstein distances may be used to detect predictive equivalences in symbolic data. We compute Wasserstein distances between distributions over sequences ("predictions"), using a finite-dimensional embedding of sequences based on the Cantor for the underlying geometry. We show that exploratory data analysis using the resulting geometry via hierarchical clustering and dimension reduction provides insight into the temporal structure of processes ranging from the relatively simple (e.g., finite-state hidden Markov models) to the very complex (e.g., infinite-state indexed grammars).

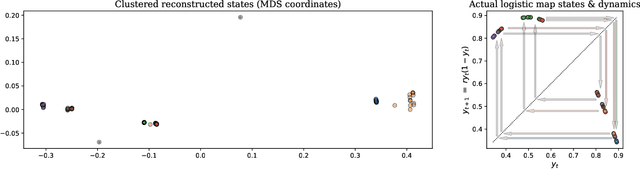
Topology, Convergence, and Reconstruction of Predictive States

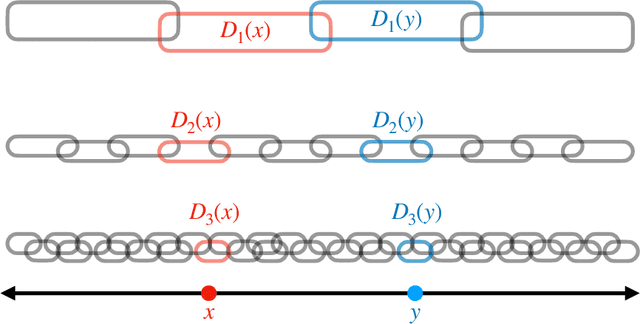
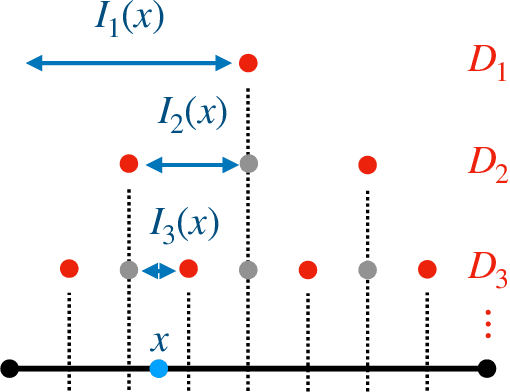
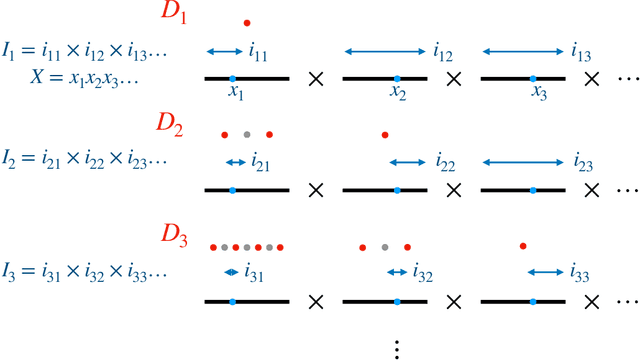
Predictive equivalence in discrete stochastic processes have been applied with great success to identify randomness and structure in statistical physics and chaotic dynamical systems and to inferring hidden Markov models. We examine the conditions under which they can be reliably reconstructed from time-series data, showing that convergence of predictive states can be achieved from empirical samples in the weak topology of measures. Moreover, predictive states may be represented in Hilbert spaces that replicate the weak topology. We mathematically explain how these representations are particularly beneficial when reconstructing high-memory processes and connect them to reproducing kernel Hilbert spaces.

Discovering Causal Structure with Reproducing-Kernel Hilbert Space $ε$-Machines

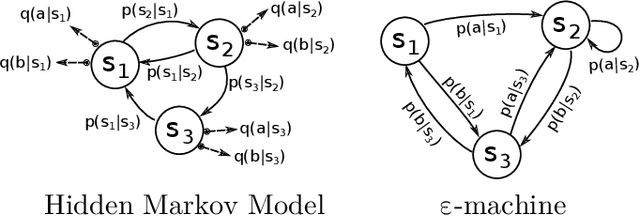
We merge computational mechanics' definition of causal states (predictively-equivalent histories) with reproducing-kernel Hilbert space (RKHS) representation inference. The result is a widely-applicable method that infers causal structure directly from observations of a system's behaviors whether they are over discrete or continuous events or time. A structural representation -- a finite- or infinite-state kernel $\epsilon$-machine -- is extracted by a reduced-dimension transform that gives an efficient representation of causal states and their topology. In this way, the system dynamics are represented by a stochastic (ordinary or partial) differential equation that acts on causal states. We introduce an algorithm to estimate the associated evolution operator. Paralleling the Fokker-Plank equation, it efficiently evolves causal-state distributions and makes predictions in the original data space via an RKHS functional mapping. We demonstrate these techniques, together with their predictive abilities, on discrete-time, discrete-value infinite Markov-order processes generated by finite-state hidden Markov models with (i) finite or (ii) uncountably-infinite causal states and (iii) a continuous-time, continuous-value process generated by a thermally-driven chaotic flow. The method robustly estimates causal structure in the presence of varying external and measurement noise levels.

Spacetime Autoencoders Using Local Causal States

Local causal states are latent representations that capture organized pattern and structure in complex spatiotemporal systems. We expand their functionality, framing them as spacetime autoencoders. Previously, they were only considered as maps from observable spacetime fields to latent local causal state fields. Here, we show that there is a stochastic decoding that maps back from the latent fields to observable fields. Furthermore, their Markovian properties define a stochastic dynamic in the latent space. Combined with stochastic decoding, this gives a new method for forecasting spacetime fields.

Shannon Entropy Rate of Hidden Markov Processes

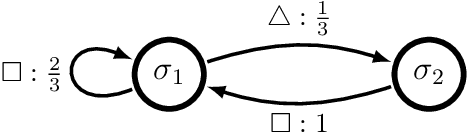
Hidden Markov chains are widely applied statistical models of stochastic processes, from fundamental physics and chemistry to finance, health, and artificial intelligence. The hidden Markov processes they generate are notoriously complicated, however, even if the chain is finite state: no finite expression for their Shannon entropy rate exists, as the set of their predictive features is generically infinite. As such, to date one cannot make general statements about how random they are nor how structured. Here, we address the first part of this challenge by showing how to efficiently and accurately calculate their entropy rates. We also show how this method gives the minimal set of infinite predictive features. A sequel addresses the challenge's second part on structure.

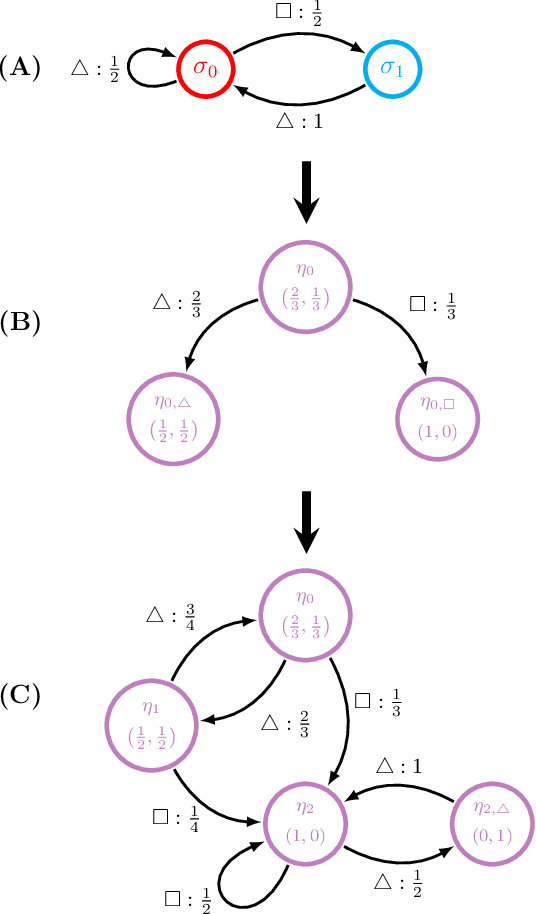
DisCo: Physics-Based Unsupervised Discovery of Coherent Structures in Spatiotemporal Systems

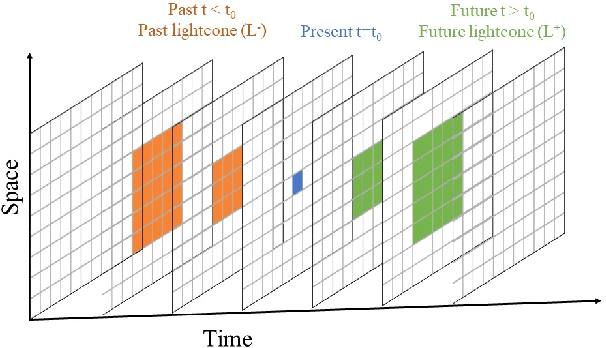
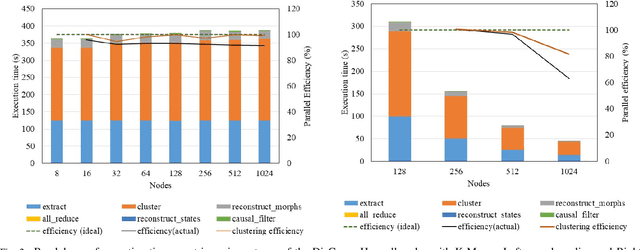
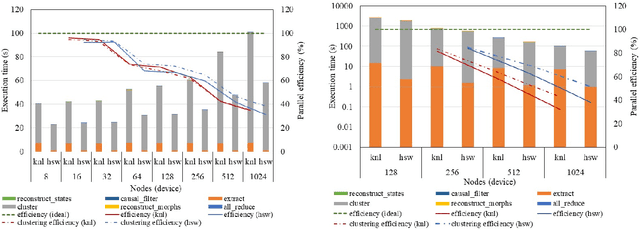
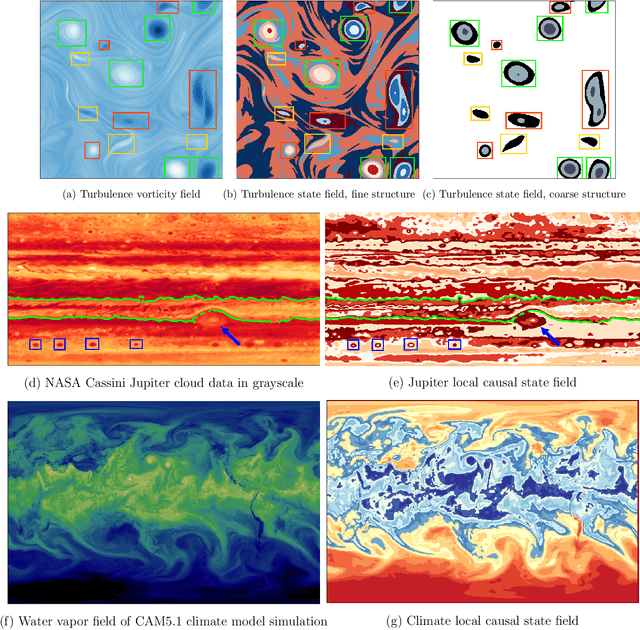
Extracting actionable insight from complex unlabeled scientific data is an open challenge and key to unlocking data-driven discovery in science. Complementary and alternative to supervised machine learning approaches, unsupervised physics-based methods based on behavior-driven theories hold great promise. Due to computational limitations, practical application on real-world domain science problems has lagged far behind theoretical development. We present our first step towards bridging this divide - DisCo - a high-performance distributed workflow for the behavior-driven local causal state theory. DisCo provides a scalable unsupervised physics-based representation learning method that decomposes spatiotemporal systems into their structurally relevant components, which are captured by the latent local causal state variables. Complex spatiotemporal systems are generally highly structured and organize around a lower-dimensional skeleton of coherent structures, and in several firsts we demonstrate the efficacy of DisCo in capturing such structures from observational and simulated scientific data. To the best of our knowledge, DisCo is also the first application software developed entirely in Python to scale to over 1000 machine nodes, providing good performance along with ensuring domain scientists' productivity. We developed scalable, performant methods optimized for Intel many-core processors that will be upstreamed to open-source Python library packages. Our capstone experiment, using newly developed DisCo workflow and libraries, performs unsupervised spacetime segmentation analysis of CAM5.1 climate simulation data, processing an unprecedented 89.5 TB in 6.6 minutes end-to-end using 1024 Intel Haswell nodes on the Cori supercomputer obtaining 91% weak-scaling and 64% strong-scaling efficiency.

Towards Unsupervised Segmentation of Extreme Weather Events

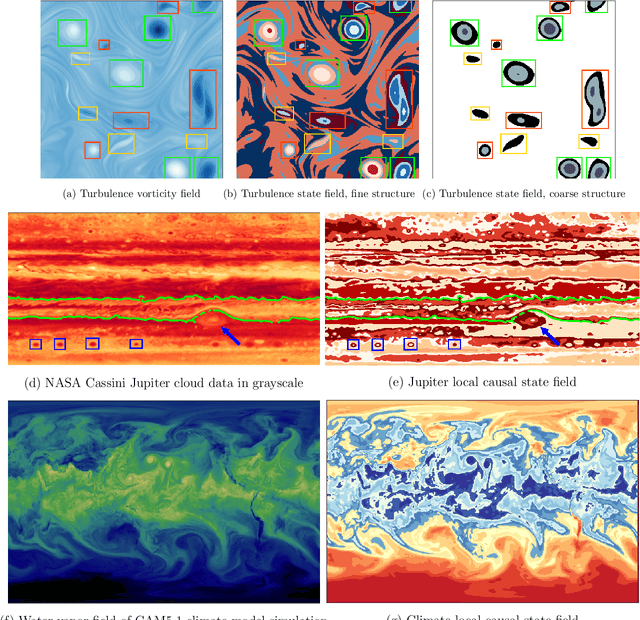
Extreme weather is one of the main mechanisms through which climate change will directly impact human society. Coping with such change as a global community requires markedly improved understanding of how global warming drives extreme weather events. While alternative climate scenarios can be simulated using sophisticated models, identifying extreme weather events in these simulations requires automation due to the vast amounts of complex high-dimensional data produced. Atmospheric dynamics, and hydrodynamic flows more generally, are highly structured and largely organize around a lower dimensional skeleton of coherent structures. Indeed, extreme weather events are a special case of more general hydrodynamic coherent structures. We present a scalable physics-based representation learning method that decomposes spatiotemporal systems into their structurally relevant components, which are captured by latent variables known as local causal states. For complex fluid flows we show our method is capable of capturing known coherent structures, and with promising segmentation results on CAM5.1 water vapor data we outline the path to extreme weather identification from unlabeled climate model simulation data.