Topology, Convergence, and Reconstruction of Predictive States
Paper and Code
Sep 19, 2021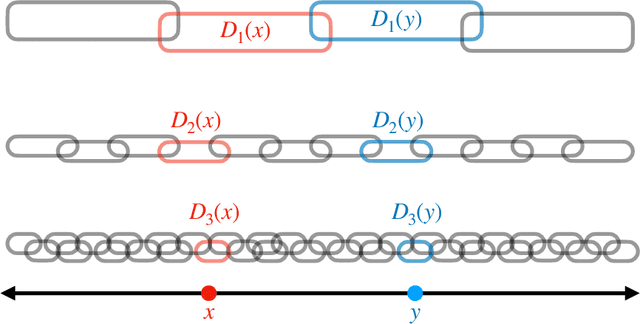
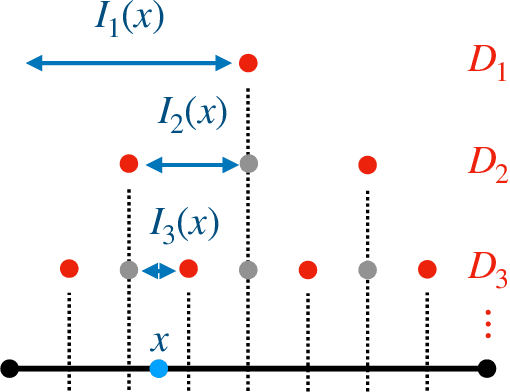
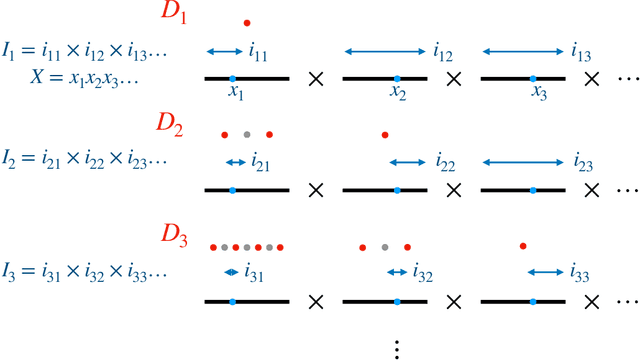

Predictive equivalence in discrete stochastic processes have been applied with great success to identify randomness and structure in statistical physics and chaotic dynamical systems and to inferring hidden Markov models. We examine the conditions under which they can be reliably reconstructed from time-series data, showing that convergence of predictive states can be achieved from empirical samples in the weak topology of measures. Moreover, predictive states may be represented in Hilbert spaces that replicate the weak topology. We mathematically explain how these representations are particularly beneficial when reconstructing high-memory processes and connect them to reproducing kernel Hilbert spaces.
* 16 pages, 4 figures; http://csc.ucdavis.edu/~cmg/papers/gartsp.pdf
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge