Paul M. Riechers
Transformers learn factored representations
Feb 02, 2026Abstract:Transformers pretrained via next token prediction learn to factor their world into parts, representing these factors in orthogonal subspaces of the residual stream. We formalize two representational hypotheses: (1) a representation in the product space of all factors, whose dimension grows exponentially with the number of parts, or (2) a factored representation in orthogonal subspaces, whose dimension grows linearly. The factored representation is lossless when factors are conditionally independent, but sacrifices predictive fidelity otherwise, creating a tradeoff between dimensional efficiency and accuracy. We derive precise predictions about the geometric structure of activations for each, including the number of subspaces, their dimensionality, and the arrangement of context embeddings within them. We test between these hypotheses on transformers trained on synthetic processes with known latent structure. Models learn factored representations when factors are conditionally independent, and continue to favor them early in training even when noise or hidden dependencies undermine conditional independence, reflecting an inductive bias toward factoring at the cost of fidelity. This provides a principled explanation for why transformers decompose the world into parts, and suggests that interpretable low dimensional structure may persist even in models trained on complex data.
Neural networks leverage nominally quantum and post-quantum representations
Jul 10, 2025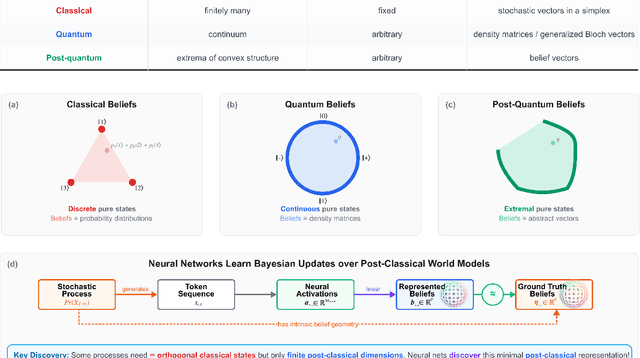
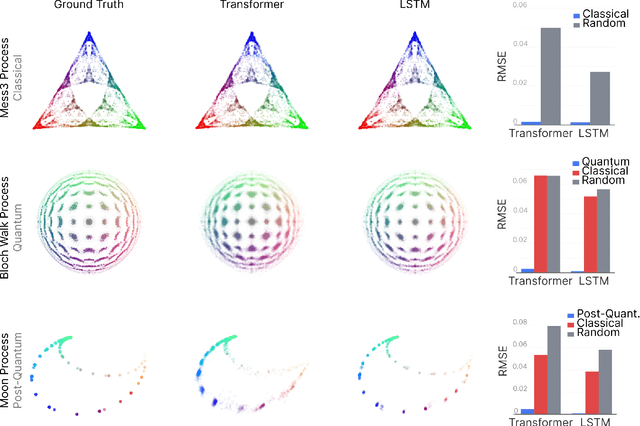
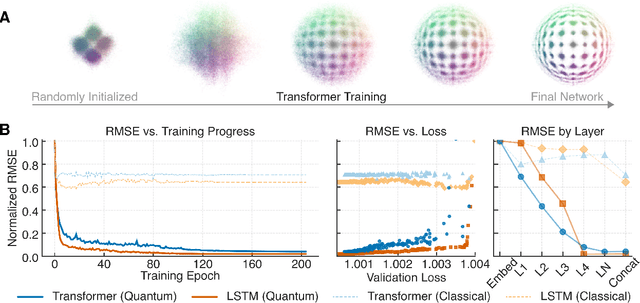
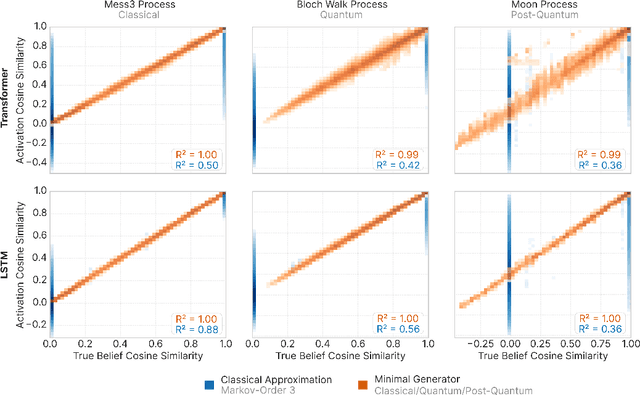
Abstract:We show that deep neural networks, including transformers and RNNs, pretrained as usual on next-token prediction, intrinsically discover and represent beliefs over 'quantum' and 'post-quantum' low-dimensional generative models of their training data -- as if performing iterative Bayesian updates over the latent state of this world model during inference as they observe more context. Notably, neural nets easily find these representation whereas there is no finite classical circuit that would do the job. The corresponding geometric relationships among neural activations induced by different input sequences are found to be largely independent of neural-network architecture. Each point in this geometry corresponds to a history-induced probability density over all possible futures, and the relative displacement of these points reflects the difference in mechanism and magnitude for how these distinct pasts affect the future.
Next-token pretraining implies in-context learning
May 23, 2025Abstract:We argue that in-context learning (ICL) predictably arises from standard self-supervised next-token pretraining, rather than being an exotic emergent property. This work establishes the foundational principles of this emergence by focusing on in-distribution ICL, demonstrating how models necessarily adapt to context when trained on token sequences, especially from non-ergodic sources. Our information-theoretic framework precisely predicts these in-distribution ICL dynamics (i.e., context-dependent loss reduction). We verify this with experiments using synthetic datasets of differing types of correlational structure, reproducing characteristic phenomena like phase transitions in training loss for induction head formation and power-law scaling of in-context loss. We further show that a model's in-context performance on any task is mathematically coupled to the ensemble of tasks seen in pretraining, offering a fundamental explanation, grounded in architecture- and modality-independent principles, for such inference-time learning.
Constrained belief updates explain geometric structures in transformer representations
Feb 04, 2025



Abstract:What computational structures emerge in transformers trained on next-token prediction? In this work, we provide evidence that transformers implement constrained Bayesian belief updating -- a parallelized version of partial Bayesian inference shaped by architectural constraints. To do this, we integrate the model-agnostic theory of optimal prediction with mechanistic interpretability to analyze transformers trained on a tractable family of hidden Markov models that generate rich geometric patterns in neural activations. We find that attention heads carry out an algorithm with a natural interpretation in the probability simplex, and create representations with distinctive geometric structure. We show how both the algorithmic behavior and the underlying geometry of these representations can be theoretically predicted in detail -- including the attention pattern, OV-vectors, and embedding vectors -- by modifying the equations for optimal future token predictions to account for the architectural constraints of attention. Our approach provides a principled lens on how gradient descent resolves the tension between optimal prediction and architectural design.
Transformers represent belief state geometry in their residual stream
May 24, 2024Abstract:What computational structure are we building into large language models when we train them on next-token prediction? Here, we present evidence that this structure is given by the meta-dynamics of belief updating over hidden states of the data-generating process. Leveraging the theory of optimal prediction, we anticipate and then find that belief states are linearly represented in the residual stream of transformers, even in cases where the predicted belief state geometry has highly nontrivial fractal structure. We investigate cases where the belief state geometry is represented in the final residual stream or distributed across the residual streams of multiple layers, providing a framework to explain these observations. Furthermore we demonstrate that the inferred belief states contain information about the entire future, beyond the local next-token prediction that the transformers are explicitly trained on. Our work provides a framework connecting the structure of training data to the computational structure and representations that transformers use to carry out their behavior.
Geometry and Dynamics of LayerNorm
May 07, 2024Abstract:A technical note aiming to offer deeper intuition for the LayerNorm function common in deep neural networks. LayerNorm is defined relative to a distinguished 'neural' basis, but it does more than just normalize the corresponding vector elements. Rather, it implements a composition -- of linear projection, nonlinear scaling, and then affine transformation -- on input activation vectors. We develop both a new mathematical expression and geometric intuition, to make the net effect more transparent. We emphasize that, when LayerNorm acts on an N-dimensional vector space, all outcomes of LayerNorm lie within the intersection of an (N-1)-dimensional hyperplane and the interior of an N-dimensional hyperellipsoid. This intersection is the interior of an (N-1)-dimensional hyperellipsoid, and typical inputs are mapped near its surface. We find the direction and length of the principal axes of this (N-1)-dimensional hyperellipsoid via the eigen-decomposition of a simply constructed matrix.
Ultimate limit on learning non-Markovian behavior: Fisher information rate and excess information
Oct 06, 2023Abstract:We address the fundamental limits of learning unknown parameters of any stochastic process from time-series data, and discover exact closed-form expressions for how optimal inference scales with observation length. Given a parametrized class of candidate models, the Fisher information of observed sequence probabilities lower-bounds the variance in model estimation from finite data. As sequence-length increases, the minimal variance scales as the square inverse of the length -- with constant coefficient given by the information rate. We discover a simple closed-form expression for this information rate, even in the case of infinite Markov order. We furthermore obtain the exact analytic lower bound on model variance from the observation-induced metadynamic among belief states. We discover ephemeral, exponential, and more general modes of convergence to the asymptotic information rate. Surprisingly, this myopic information rate converges to the asymptotic Fisher information rate with exactly the same relaxation timescales that appear in the myopic entropy rate as it converges to the Shannon entropy rate for the process. We illustrate these results with a sequence of examples that highlight qualitatively distinct features of stochastic processes that shape optimal learning.
Complexity-calibrated Benchmarks for Machine Learning Reveal When Next-Generation Reservoir Computer Predictions Succeed and Mislead
Mar 25, 2023Abstract:Recurrent neural networks are used to forecast time series in finance, climate, language, and from many other domains. Reservoir computers are a particularly easily trainable form of recurrent neural network. Recently, a "next-generation" reservoir computer was introduced in which the memory trace involves only a finite number of previous symbols. We explore the inherent limitations of finite-past memory traces in this intriguing proposal. A lower bound from Fano's inequality shows that, on highly non-Markovian processes generated by large probabilistic state machines, next-generation reservoir computers with reasonably long memory traces have an error probability that is at least ~ 60% higher than the minimal attainable error probability in predicting the next observation. More generally, it appears that popular recurrent neural networks fall far short of optimally predicting such complex processes. These results highlight the need for a new generation of optimized recurrent neural network architectures. Alongside this finding, we present concentration-of-measure results for randomly-generated but complex processes. One conclusion is that large probabilistic state machines -- specifically, large $\epsilon$-machines -- are key to generating challenging and structurally-unbiased stimuli for ground-truthing recurrent neural network architectures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge