Adam S. Shai
Neural networks leverage nominally quantum and post-quantum representations
Jul 10, 2025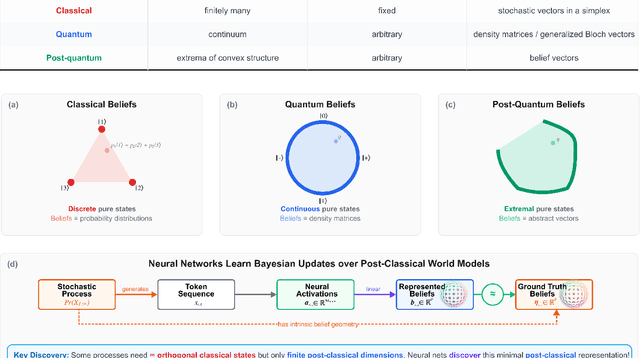
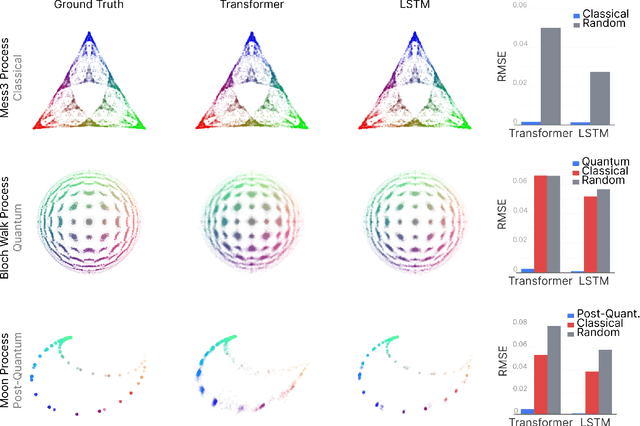
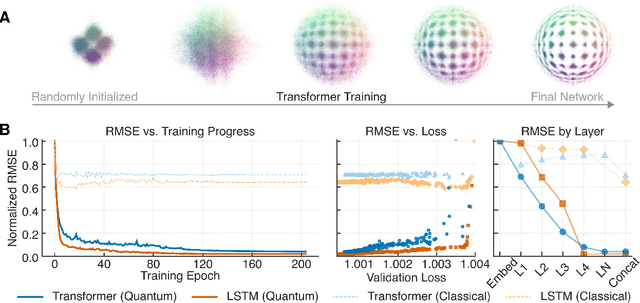
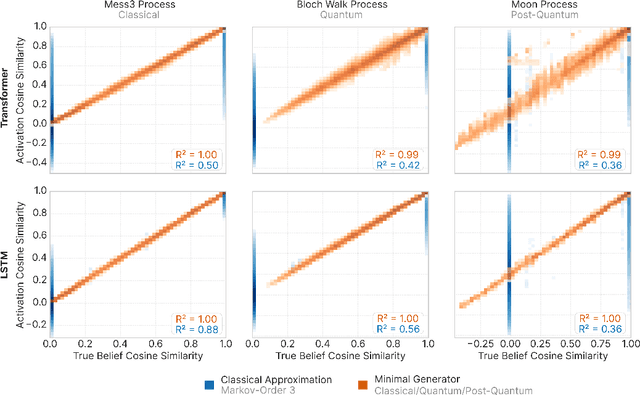
Abstract:We show that deep neural networks, including transformers and RNNs, pretrained as usual on next-token prediction, intrinsically discover and represent beliefs over 'quantum' and 'post-quantum' low-dimensional generative models of their training data -- as if performing iterative Bayesian updates over the latent state of this world model during inference as they observe more context. Notably, neural nets easily find these representation whereas there is no finite classical circuit that would do the job. The corresponding geometric relationships among neural activations induced by different input sequences are found to be largely independent of neural-network architecture. Each point in this geometry corresponds to a history-induced probability density over all possible futures, and the relative displacement of these points reflects the difference in mechanism and magnitude for how these distinct pasts affect the future.
Constrained belief updates explain geometric structures in transformer representations
Feb 04, 2025



Abstract:What computational structures emerge in transformers trained on next-token prediction? In this work, we provide evidence that transformers implement constrained Bayesian belief updating -- a parallelized version of partial Bayesian inference shaped by architectural constraints. To do this, we integrate the model-agnostic theory of optimal prediction with mechanistic interpretability to analyze transformers trained on a tractable family of hidden Markov models that generate rich geometric patterns in neural activations. We find that attention heads carry out an algorithm with a natural interpretation in the probability simplex, and create representations with distinctive geometric structure. We show how both the algorithmic behavior and the underlying geometry of these representations can be theoretically predicted in detail -- including the attention pattern, OV-vectors, and embedding vectors -- by modifying the equations for optimal future token predictions to account for the architectural constraints of attention. Our approach provides a principled lens on how gradient descent resolves the tension between optimal prediction and architectural design.
Transformers represent belief state geometry in their residual stream
May 24, 2024Abstract:What computational structure are we building into large language models when we train them on next-token prediction? Here, we present evidence that this structure is given by the meta-dynamics of belief updating over hidden states of the data-generating process. Leveraging the theory of optimal prediction, we anticipate and then find that belief states are linearly represented in the residual stream of transformers, even in cases where the predicted belief state geometry has highly nontrivial fractal structure. We investigate cases where the belief state geometry is represented in the final residual stream or distributed across the residual streams of multiple layers, providing a framework to explain these observations. Furthermore we demonstrate that the inferred belief states contain information about the entire future, beyond the local next-token prediction that the transformers are explicitly trained on. Our work provides a framework connecting the structure of training data to the computational structure and representations that transformers use to carry out their behavior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge