Daniel Filan
Constrained belief updates explain geometric structures in transformer representations
Feb 04, 2025



Abstract:What computational structures emerge in transformers trained on next-token prediction? In this work, we provide evidence that transformers implement constrained Bayesian belief updating -- a parallelized version of partial Bayesian inference shaped by architectural constraints. To do this, we integrate the model-agnostic theory of optimal prediction with mechanistic interpretability to analyze transformers trained on a tractable family of hidden Markov models that generate rich geometric patterns in neural activations. We find that attention heads carry out an algorithm with a natural interpretation in the probability simplex, and create representations with distinctive geometric structure. We show how both the algorithmic behavior and the underlying geometry of these representations can be theoretically predicted in detail -- including the attention pattern, OV-vectors, and embedding vectors -- by modifying the equations for optimal future token predictions to account for the architectural constraints of attention. Our approach provides a principled lens on how gradient descent resolves the tension between optimal prediction and architectural design.
Detecting Modularity in Deep Neural Networks
Oct 13, 2021



Abstract:A neural network is modular to the extent that parts of its computational graph (i.e. structure) can be represented as performing some comprehensible subtask relevant to the overall task (i.e. functionality). Are modern deep neural networks modular? How can this be quantified? In this paper, we consider the problem of assessing the modularity exhibited by a partitioning of a network's neurons. We propose two proxies for this: importance, which reflects how crucial sets of neurons are to network performance; and coherence, which reflects how consistently their neurons associate with features of the inputs. To measure these proxies, we develop a set of statistical methods based on techniques conventionally used to interpret individual neurons. We apply the proxies to partitionings generated by spectrally clustering a graph representation of the network's neurons with edges determined either by network weights or correlations of activations. We show that these partitionings, even ones based only on weights (i.e. strictly from non-runtime analysis), reveal groups of neurons that are important and coherent. These results suggest that graph-based partitioning can reveal modularity and help us understand how deep neural networks function.
Clusterability in Neural Networks
Mar 04, 2021

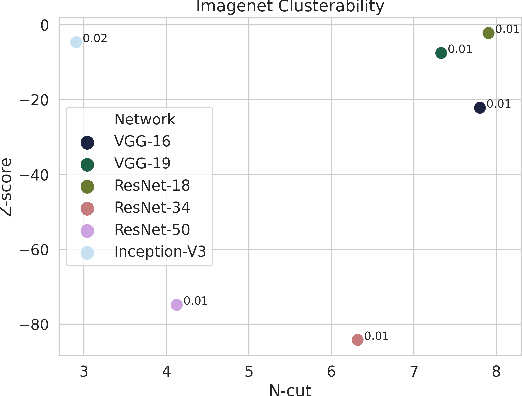

Abstract:The learned weights of a neural network have often been considered devoid of scrutable internal structure. In this paper, however, we look for structure in the form of clusterability: how well a network can be divided into groups of neurons with strong internal connectivity but weak external connectivity. We find that a trained neural network is typically more clusterable than randomly initialized networks, and often clusterable relative to random networks with the same distribution of weights. We also exhibit novel methods to promote clusterability in neural network training, and find that in multi-layer perceptrons they lead to more clusterable networks with little reduction in accuracy. Understanding and controlling the clusterability of neural networks will hopefully render their inner workings more interpretable to engineers by facilitating partitioning into meaningful clusters.
Neural Networks are Surprisingly Modular
Mar 11, 2020



Abstract:The learned weights of a neural network are often considered devoid of scrutable internal structure. In order to attempt to discern structure in these weights, we introduce a measurable notion of modularity for multi-layer perceptrons (MLPs), and investigate the modular structure of MLPs trained on datasets of small images. Our notion of modularity comes from the graph clustering literature: a "module" is a set of neurons with strong internal connectivity but weak external connectivity. We find that MLPs that undergo training and weight pruning are often significantly more modular than random networks with the same distribution of weights. Interestingly, they are much more modular when trained with dropout. Further analysis shows that this modularity seems to arise mostly for networks trained on learnable datasets. We also present exploratory analyses of the importance of different modules for performance and how modules depend on each other. Understanding the modular structure of neural networks, when such structure exists, will hopefully render their inner workings more interpretable to engineers.
Exploring Hierarchy-Aware Inverse Reinforcement Learning
Jul 13, 2018



Abstract:We introduce a new generative model for human planning under the Bayesian Inverse Reinforcement Learning (BIRL) framework which takes into account the fact that humans often plan using hierarchical strategies. We describe the Bayesian Inverse Hierarchical RL (BIHRL) algorithm for inferring the values of hierarchical planners, and use an illustrative toy model to show that BIHRL retains accuracy where standard BIRL fails. Furthermore, BIHRL is able to accurately predict the goals of `Wikispeedia' game players, with inclusion of hierarchical structure in the model resulting in a large boost in accuracy. We show that BIHRL is able to significantly outperform BIRL even when we only have a weak prior on the hierarchical structure of the plans available to the agent, and discuss the significant challenges that remain for scaling up this framework to more realistic settings.
* Presented at the first Workshop on Goal Specifications for Reinforcement Learning, ICML 2018, Stockholm, Sweden
Self-Modification of Policy and Utility Function in Rational Agents
May 10, 2016


Abstract:Any agent that is part of the environment it interacts with and has versatile actuators (such as arms and fingers), will in principle have the ability to self-modify -- for example by changing its own source code. As we continue to create more and more intelligent agents, chances increase that they will learn about this ability. The question is: will they want to use it? For example, highly intelligent systems may find ways to change their goals to something more easily achievable, thereby `escaping' the control of their designers. In an important paper, Omohundro (2008) argued that goal preservation is a fundamental drive of any intelligent system, since a goal is more likely to be achieved if future versions of the agent strive towards the same goal. In this paper, we formalise this argument in general reinforcement learning, and explore situations where it fails. Our conclusion is that the self-modification possibility is harmless if and only if the value function of the agent anticipates the consequences of self-modifications and use the current utility function when evaluating the future.
Loss Bounds and Time Complexity for Speed Priors
Apr 12, 2016Abstract:This paper establishes for the first time the predictive performance of speed priors and their computational complexity. A speed prior is essentially a probability distribution that puts low probability on strings that are not efficiently computable. We propose a variant to the original speed prior (Schmidhuber, 2002), and show that our prior can predict sequences drawn from probability measures that are estimable in polynomial time. Our speed prior is computable in doubly-exponential time, but not in polynomial time. On a polynomial time computable sequence our speed prior is computable in exponential time. We show better upper complexity bounds for Schmidhuber's speed prior under the same conditions, and that it predicts deterministic sequences that are computable in polynomial time; however, we also show that it is not computable in polynomial time, and the question of its predictive properties for stochastic sequences remains open.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge