Do You Really Need Public Data? Surrogate Public Data for Differential Privacy on Tabular Data

Differentially private (DP) machine learning often relies on the availability of public data for tasks like privacy-utility trade-off estimation, hyperparameter tuning, and pretraining. While public data assumptions may be reasonable in text and image domains, they are less likely to hold for tabular data due to tabular data heterogeneity across domains. We propose leveraging powerful priors to address this limitation; specifically, we synthesize realistic tabular data directly from schema-level specifications - such as variable names, types, and permissible ranges - without ever accessing sensitive records. To that end, this work introduces the notion of "surrogate" public data - datasets generated independently of sensitive data, which consume no privacy loss budget and are constructed solely from publicly available schema or metadata. Surrogate public data are intended to encode plausible statistical assumptions (informed by publicly available information) into a dataset with many downstream uses in private mechanisms. We automate the process of generating surrogate public data with large language models (LLMs); in particular, we propose two methods: direct record generation as CSV files, and automated structural causal model (SCM) construction for sampling records. Through extensive experiments, we demonstrate that surrogate public tabular data can effectively replace traditional public data when pretraining differentially private tabular classifiers. To a lesser extent, surrogate public data are also useful for hyperparameter tuning of DP synthetic data generators, and for estimating the privacy-utility tradeoff.

Detecting Modularity in Deep Neural Networks

A neural network is modular to the extent that parts of its computational graph (i.e. structure) can be represented as performing some comprehensible subtask relevant to the overall task (i.e. functionality). Are modern deep neural networks modular? How can this be quantified? In this paper, we consider the problem of assessing the modularity exhibited by a partitioning of a network's neurons. We propose two proxies for this: importance, which reflects how crucial sets of neurons are to network performance; and coherence, which reflects how consistently their neurons associate with features of the inputs. To measure these proxies, we develop a set of statistical methods based on techniques conventionally used to interpret individual neurons. We apply the proxies to partitionings generated by spectrally clustering a graph representation of the network's neurons with edges determined either by network weights or correlations of activations. We show that these partitionings, even ones based only on weights (i.e. strictly from non-runtime analysis), reveal groups of neurons that are important and coherent. These results suggest that graph-based partitioning can reveal modularity and help us understand how deep neural networks function.

Clusterability in Neural Networks

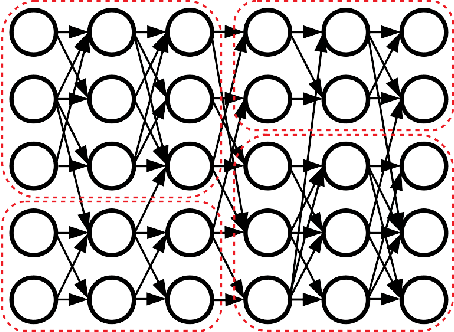
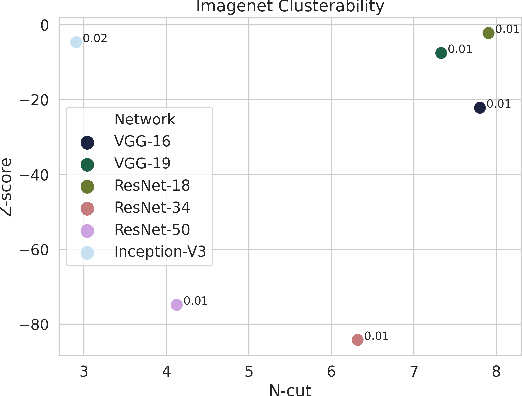
The learned weights of a neural network have often been considered devoid of scrutable internal structure. In this paper, however, we look for structure in the form of clusterability: how well a network can be divided into groups of neurons with strong internal connectivity but weak external connectivity. We find that a trained neural network is typically more clusterable than randomly initialized networks, and often clusterable relative to random networks with the same distribution of weights. We also exhibit novel methods to promote clusterability in neural network training, and find that in multi-layer perceptrons they lead to more clusterable networks with little reduction in accuracy. Understanding and controlling the clusterability of neural networks will hopefully render their inner workings more interpretable to engineers by facilitating partitioning into meaningful clusters.

Performative Prediction in a Stateful World

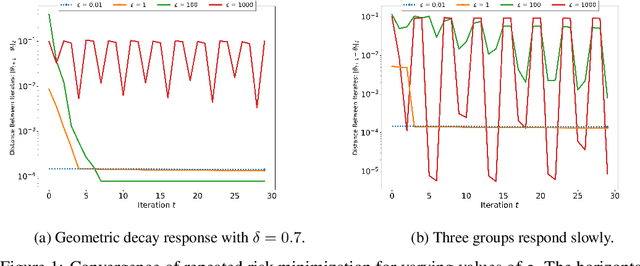
Deployed supervised machine learning models make predictions that interact with and influence the world. This phenomenon is called "performative prediction" by Perdomo et al. (2020), who investigated it in a stateless setting. We generalize their results to the case where the response of the population to the deployed classifier depends both on the classifier and the previous distribution of the population. We also demonstrate such a setting empirically, for the scenario of strategic manipulation.

Neural Networks are Surprisingly Modular

The learned weights of a neural network are often considered devoid of scrutable internal structure. In order to attempt to discern structure in these weights, we introduce a measurable notion of modularity for multi-layer perceptrons (MLPs), and investigate the modular structure of MLPs trained on datasets of small images. Our notion of modularity comes from the graph clustering literature: a "module" is a set of neurons with strong internal connectivity but weak external connectivity. We find that MLPs that undergo training and weight pruning are often significantly more modular than random networks with the same distribution of weights. Interestingly, they are much more modular when trained with dropout. Further analysis shows that this modularity seems to arise mostly for networks trained on learnable datasets. We also present exploratory analyses of the importance of different modules for performance and how modules depend on each other. Understanding the modular structure of neural networks, when such structure exists, will hopefully render their inner workings more interpretable to engineers.