Insufficient Statistics Perturbation: Stable Estimators for Private Least Squares

We present a sample- and time-efficient differentially private algorithm for ordinary least squares, with error that depends linearly on the dimension and is independent of the condition number of $X^\top X$, where $X$ is the design matrix. All prior private algorithms for this task require either $d^{3/2}$ examples, error growing polynomially with the condition number, or exponential time. Our near-optimal accuracy guarantee holds for any dataset with bounded statistical leverage and bounded residuals. Technically, we build on the approach of Brown et al. (2023) for private mean estimation, adding scaled noise to a carefully designed stable nonprivate estimator of the empirical regression vector.

Private Gradient Descent for Linear Regression: Tighter Error Bounds and Instance-Specific Uncertainty Estimation

We provide an improved analysis of standard differentially private gradient descent for linear regression under the squared error loss. Under modest assumptions on the input, we characterize the distribution of the iterate at each time step. Our analysis leads to new results on the algorithm's accuracy: for a proper fixed choice of hyperparameters, the sample complexity depends only linearly on the dimension of the data. This matches the dimension-dependence of the (non-private) ordinary least squares estimator as well as that of recent private algorithms that rely on sophisticated adaptive gradient-clipping schemes (Varshney et al., 2022; Liu et al., 2023). Our analysis of the iterates' distribution also allows us to construct confidence intervals for the empirical optimizer which adapt automatically to the variance of the algorithm on a particular data set. We validate our theorems through experiments on synthetic data.

Metalearning with Very Few Samples Per Task

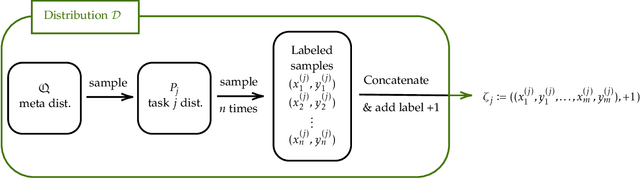
Metalearning and multitask learning are two frameworks for solving a group of related learning tasks more efficiently than we could hope to solve each of the individual tasks on their own. In multitask learning, we are given a fixed set of related learning tasks and need to output one accurate model per task, whereas in metalearning we are given tasks that are drawn i.i.d. from a metadistribution and need to output some common information that can be easily specialized to new, previously unseen tasks from the metadistribution. In this work, we consider a binary classification setting where tasks are related by a shared representation, that is, every task $P$ of interest can be solved by a classifier of the form $f_{P} \circ h$ where $h \in H$ is a map from features to some representation space that is shared across tasks, and $f_{P} \in F$ is a task-specific classifier from the representation space to labels. The main question we ask in this work is how much data do we need to metalearn a good representation? Here, the amount of data is measured in terms of both the number of tasks $t$ that we need to see and the number of samples $n$ per task. We focus on the regime where the number of samples per task is extremely small. Our main result shows that, in a distribution-free setting where the feature vectors are in $\mathbb{R}^d$, the representation is a linear map from $\mathbb{R}^d \to \mathbb{R}^k$, and the task-specific classifiers are halfspaces in $\mathbb{R}^k$, we can metalearn a representation with error $\varepsilon$ using just $n = k+2$ samples per task, and $d \cdot (1/\varepsilon)^{O(k)}$ tasks. Learning with so few samples per task is remarkable because metalearning would be impossible with $k+1$ samples per task, and because we cannot even hope to learn an accurate task-specific classifier with just $k+2$ samples per task.

A max-affine spline approximation of neural networks using the Legendre transform of a convex-concave representation

This work presents a novel algorithm for transforming a neural network into a spline representation. Unlike previous work that required convex and piecewise-affine network operators to create a max-affine spline alternate form, this work relaxes this constraint. The only constraint is that the function be bounded and possess a well-define second derivative, although this was shown experimentally to not be strictly necessary. It can also be performed over the whole network rather than on each layer independently. As in previous work, this bridges the gap between neural networks and approximation theory but also enables the visualisation of network feature maps. Mathematical proof and experimental investigation of the technique is performed with approximation error and feature maps being extracted from a range of architectures, including convolutional neural networks.

Tiny Classifier Circuits: Evolving Accelerators for Tabular Data

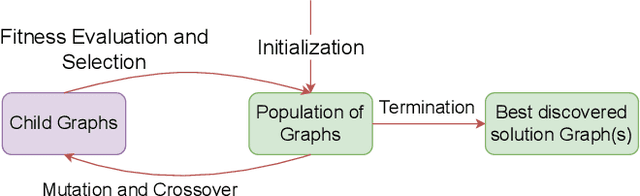
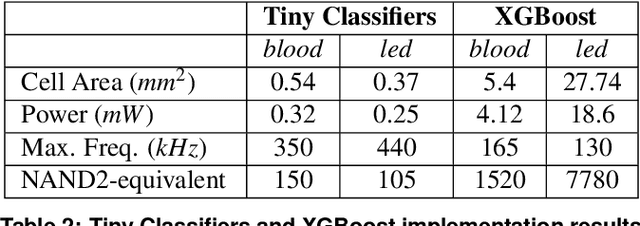
A typical machine learning (ML) development cycle for edge computing is to maximise the performance during model training and then minimise the memory/area footprint of the trained model for deployment on edge devices targeting CPUs, GPUs, microcontrollers, or custom hardware accelerators. This paper proposes a methodology for automatically generating predictor circuits for classification of tabular data with comparable prediction performance to conventional ML techniques while using substantially fewer hardware resources and power. The proposed methodology uses an evolutionary algorithm to search over the space of logic gates and automatically generates a classifier circuit with maximised training prediction accuracy. Classifier circuits are so tiny (i.e., consisting of no more than 300 logic gates) that they are called "Tiny Classifier" circuits, and can efficiently be implemented in ASIC or on an FPGA. We empirically evaluate the automatic Tiny Classifier circuit generation methodology or "Auto Tiny Classifiers" on a wide range of tabular datasets, and compare it against conventional ML techniques such as Amazon's AutoGluon, Google's TabNet and a neural search over Multi-Layer Perceptrons. Despite Tiny Classifiers being constrained to a few hundred logic gates, we observe no statistically significant difference in prediction performance in comparison to the best-performing ML baseline. When synthesised as a Silicon chip, Tiny Classifiers use 8-56x less area and 4-22x less power. When implemented as an ultra-low cost chip on a flexible substrate (i.e., FlexIC), they occupy 10-75x less area and consume 13-75x less power compared to the most hardware-efficient ML baseline. On an FPGA, Tiny Classifiers consume 3-11x fewer resources.

Fast, Sample-Efficient, Affine-Invariant Private Mean and Covariance Estimation for Subgaussian Distributions

We present a fast, differentially private algorithm for high-dimensional covariance-aware mean estimation with nearly optimal sample complexity. Only exponential-time estimators were previously known to achieve this guarantee. Given $n$ samples from a (sub-)Gaussian distribution with unknown mean $\mu$ and covariance $\Sigma$, our $(\varepsilon,\delta)$-differentially private estimator produces $\tilde{\mu}$ such that $\|\mu - \tilde{\mu}\|_{\Sigma} \leq \alpha$ as long as $n \gtrsim \tfrac d {\alpha^2} + \tfrac{d \sqrt{\log 1/\delta}}{\alpha \varepsilon}+\frac{d\log 1/\delta}{\varepsilon}$. The Mahalanobis error metric $\|\mu - \hat{\mu}\|_{\Sigma}$ measures the distance between $\hat \mu$ and $\mu$ relative to $\Sigma$; it characterizes the error of the sample mean. Our algorithm runs in time $\tilde{O}(nd^{\omega - 1} + nd/\varepsilon)$, where $\omega < 2.38$ is the matrix multiplication exponent. We adapt an exponential-time approach of Brown, Gaboardi, Smith, Ullman, and Zakynthinou (2021), giving efficient variants of stable mean and covariance estimation subroutines that also improve the sample complexity to the nearly optimal bound above. Our stable covariance estimator can be turned to private covariance estimation for unrestricted subgaussian distributions. With $n\gtrsim d^{3/2}$ samples, our estimate is accurate in spectral norm. This is the first such algorithm using $n= o(d^2)$ samples, answering an open question posed by Alabi et al. (2022). With $n\gtrsim d^2$ samples, our estimate is accurate in Frobenius norm. This leads to a fast, nearly optimal algorithm for private learning of unrestricted Gaussian distributions in TV distance. Duchi, Haque, and Kuditipudi (2023) obtained similar results independently and concurrently.

A Unified Theory of Diversity in Ensemble Learning

We present a theory of ensemble diversity, explaining the nature and effect of diversity for a wide range of supervised learning scenarios. This challenge, of understanding ensemble diversity, has been referred to as the holy grail of ensemble learning, an open question for over 30 years. Our framework reveals that diversity is in fact a hidden dimension in the bias-variance decomposition of an ensemble. In particular, we prove a family of exact bias-variance-diversity decompositions, for both classification and regression losses, e.g., squared, and cross-entropy. The framework provides a methodology to automatically identify the combiner rule enabling such a decomposition, specific to the loss. The formulation of diversity is therefore dependent on just two design choices: the loss, and the combiner. For certain choices (e.g., 0-1 loss with majority voting) the effect of diversity is necessarily dependent on the target label. Experiments illustrate how we can use our framework to understand the diversity-encouraging mechanisms of popular ensemble methods: Bagging, Boosting, and Random Forests.

Outlier detection of vital sign trajectories from COVID-19 patients

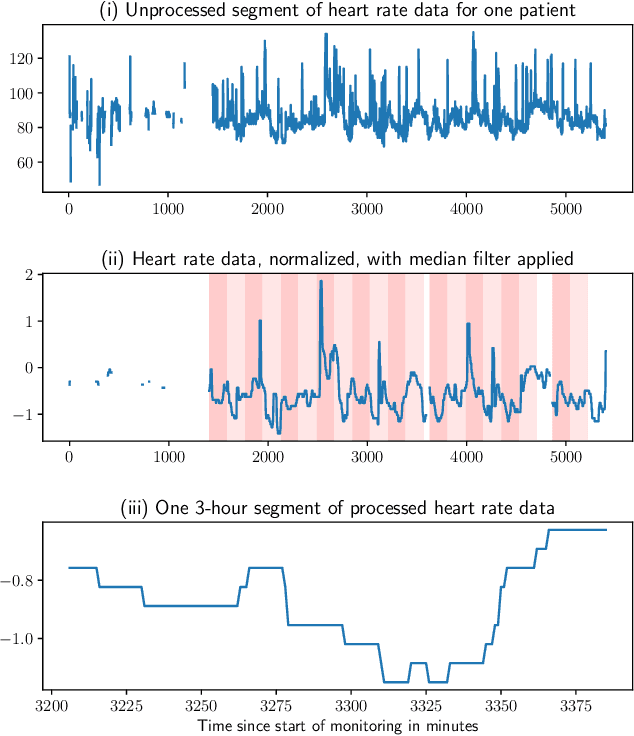
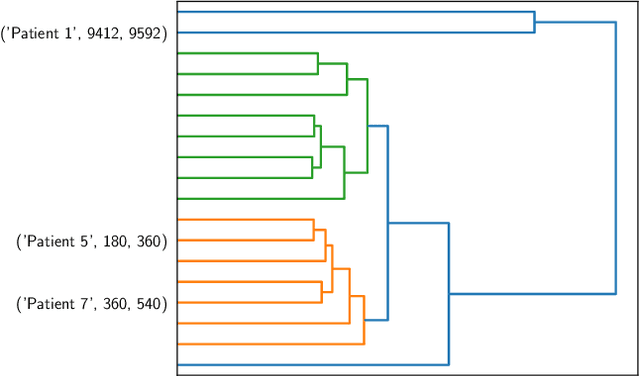
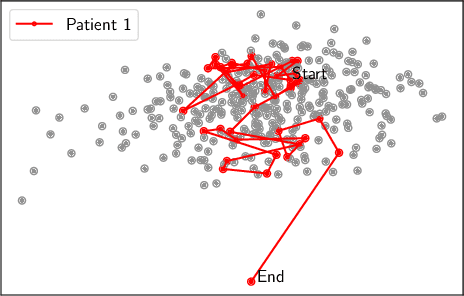
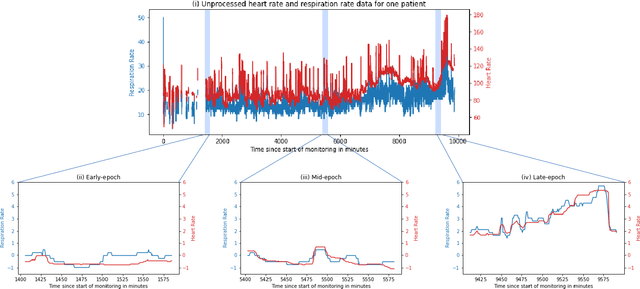
There is growing interest in continuous wearable vital sign sensors for monitoring patients remotely at home. These monitors are usually coupled to an alerting system, which is triggered when vital sign measurements fall outside a predefined normal range. Trends in vital signs, such as an increasing heart rate, are often indicative of deteriorating health, but are rarely incorporated into alerting systems. In this work, we present a novel outlier detection algorithm to identify such abnormal vital sign trends. We introduce a distance-based measure to compare vital sign trajectories. For each patient in our dataset, we split vital sign time series into 180 minute, non-overlapping epochs. We then calculated a distance between all pairs of epochs using the dynamic time warp distance. Each epoch was characterized by its mean pairwise distance (average link distance) to all other epochs, with large distances considered as outliers. We applied this method to a pilot dataset collected over 1561 patient-hours from 8 patients who had recently been discharged from hospital after contracting COVID-19. We show that outlier epochs correspond well with patients who were subsequently readmitted to hospital. We also show, descriptively, how epochs transition from normal to abnormal for one such patient.

Strong Memory Lower Bounds for Learning Natural Models

We give lower bounds on the amount of memory required by one-pass streaming algorithms for solving several natural learning problems. In a setting where examples lie in $\{0,1\}^d$ and the optimal classifier can be encoded using $\kappa$ bits, we show that algorithms which learn using a near-minimal number of examples, $\tilde O(\kappa)$, must use $\tilde \Omega( d\kappa)$ bits of space. Our space bounds match the dimension of the ambient space of the problem's natural parametrization, even when it is quadratic in the size of examples and the final classifier. For instance, in the setting of $d$-sparse linear classifiers over degree-2 polynomial features, for which $\kappa=\Theta(d\log d)$, our space lower bound is $\tilde\Omega(d^2)$. Our bounds degrade gracefully with the stream length $N$, generally having the form $\tilde\Omega\left(d\kappa \cdot \frac{\kappa}{N}\right)$. Bounds of the form $\Omega(d\kappa)$ were known for learning parity and other problems defined over finite fields. Bounds that apply in a narrow range of sample sizes are also known for linear regression. Ours are the first such bounds for problems of the type commonly seen in recent learning applications that apply for a large range of input sizes.

Bias-Variance Decompositions for Margin Losses

We introduce a novel bias-variance decomposition for a range of strictly convex margin losses, including the logistic loss (minimized by the classic LogitBoost algorithm), as well as the squared margin loss and canonical boosting loss. Furthermore, we show that, for all strictly convex margin losses, the expected risk decomposes into the risk of a "central" model and a term quantifying variation in the functional margin with respect to variations in the training data. These decompositions provide a diagnostic tool for practitioners to understand model overfitting/underfitting, and have implications for additive ensemble models -- for example, when our bias-variance decomposition holds, there is a corresponding "ambiguity" decomposition, which can be used to quantify model diversity.