Optimal Prediction-Augmented Algorithms for Testing Independence of Distributions

Independence testing is a fundamental problem in statistical inference: given samples from a joint distribution $p$ over multiple random variables, the goal is to determine whether $p$ is a product distribution or is $ε$-far from all product distributions in total variation distance. In the non-parametric finite-sample regime, this task is notoriously expensive, as the minimax sample complexity scales polynomially with the support size. In this work, we move beyond these worst-case limitations by leveraging the framework of \textit{augmented distribution testing}. We design independence testers that incorporate auxiliary, but potentially untrustworthy, predictive information. Our framework ensures that the tester remains robust, maintaining worst-case validity regardless of the prediction's quality, while significantly improving sample efficiency when the prediction is accurate. Our main contributions include: (i) a bivariate independence tester for discrete distributions that adaptively reduces sample complexity based on the prediction error; (ii) a generalization to the high-dimensional multivariate setting for testing the independence of $d$ random variables; and (iii) matching minimax lower bounds demonstrating that our testers achieve optimal sample complexity.

High-Dimensional Robust Mean Estimation with Untrusted Batches

We study high-dimensional mean estimation in a collaborative setting where data is contributed by $N$ users in batches of size $n$. In this environment, a learner seeks to recover the mean $μ$ of a true distribution $P$ from a collection of sources that are both statistically heterogeneous and potentially malicious. We formalize this challenge through a double corruption landscape: an $\varepsilon$-fraction of users are entirely adversarial, while the remaining ``good'' users provide data from distributions that are related to $P$, but deviate by a proximity parameter $α$. Unlike existing work on the untrusted batch model, which typically measures this deviation via total variation distance in discrete settings, we address the continuous, high-dimensional regime under two natural variants for deviation: (1) good batches are drawn from distributions with a mean-shift of $\sqrtα$, or (2) an $α$-fraction of samples within each good batch are adversarially corrupted. In particular, the second model presents significant new challenges: in high dimensions, unlike discrete settings, even a small fraction of sample-level corruption can shift empirical means and covariances arbitrarily. We provide two Sum-of-Squares (SoS) based algorithms to navigate this tiered corruption. Our algorithms achieve the minimax-optimal error rate $O(\sqrt{\varepsilon/n} + \sqrt{d/nN} + \sqrtα)$, demonstrating that while heterogeneity $α$ represents an inherent statistical difficulty, the influence of adversarial users is suppressed by a factor of $1/\sqrt{n}$ due to the internal averaging afforded by the batch structure.

Support Basis: Fast Attention Beyond Bounded Entries

The quadratic complexity of softmax attention remains a central bottleneck in scaling large language models (LLMs). [Alman and Song, NeurIPS 2023] proposed a sub-quadratic attention approximation algorithm, but it works only under the restrictive bounded-entry assumption. Since this assumption rarely holds in practice, its applicability to modern LLMs is limited. In this paper, we introduce support-basis decomposition, a new framework for efficient attention approximation beyond bounded entries. We empirically demonstrate that the entries of the query and key matrices exhibit sub-Gaussian behavior. Our approach uses this property to split large and small entries, enabling exact computation on sparse components and polynomial approximation on dense components. We establish rigorous theoretical guarantees, proving a sub-quadratic runtime, and extend the method to a multi-threshold setting that eliminates all distributional assumptions. Furthermore, we provide the first theoretical justification for the empirical success of polynomial attention [Kacham, Mirrokni, and Zhong, ICML 2024], showing that softmax attention can be closely approximated by a combination of multiple polynomial attentions with sketching.

Hypothesis Selection: A High Probability Conundrum

In the hypothesis selection problem, we are given a finite set of candidate distributions (hypotheses), $\mathcal{H} = \{H_1, \ldots, H_n\}$, and samples from an unknown distribution $P$. Our goal is to find a hypothesis $H_i$ whose total variation distance to $P$ is comparable to that of the nearest hypothesis in $\mathcal{H}$. If the minimum distance is $\mathsf{OPT}$, we aim to output an $H_i$ such that, with probability at least $1-\delta$, its total variation distance to $P$ is at most $C \cdot \mathsf{OPT} + \varepsilon$. Despite decades of work, key aspects of this problem remain unresolved, including the optimal running time for algorithms that achieve the optimal sample complexity and best possible approximation factor of $C=3$. The previous state-of-the-art result [Aliakbarpour, Bun, Smith, NeurIPS 2024] provided a nearly linear in $n$ time algorithm but with a sub-optimal dependence on the other parameters, running in $\tilde{O}(n/(\delta^3\varepsilon^3))$ time. We improve this time complexity to $\tilde{O}(n/(\delta \varepsilon^2))$, significantly reducing the dependence on the confidence and error parameters. Furthermore, we study hypothesis selection in three alternative settings, resolving or making progress on several open questions from prior works. (1) We settle the optimal approximation factor when bounding the \textit{expected distance} of the output hypothesis, rather than its high-probability performance. (2) Assuming the numerical value of \textit{$\mathsf{OPT}$ is known} in advance, we present an algorithm obtaining $C=3$ and runtime $\tilde{O}(n/\varepsilon^2)$ with the optimal sample complexity and succeeding with high probability in $n$. (3) Allowing polynomial \textit{preprocessing} step on the hypothesis class $\mathcal{H}$ before observing samples, we present an algorithm with $C=3$ and subquadratic runtime which succeeds with high probability in $n$.

Better Private Distribution Testing by Leveraging Unverified Auxiliary Data

We extend the framework of augmented distribution testing (Aliakbarpour, Indyk, Rubinfeld, and Silwal, NeurIPS 2024) to the differentially private setting. This captures scenarios where a data analyst must perform hypothesis testing tasks on sensitive data, but is able to leverage prior knowledge (public, but possibly erroneous or untrusted) about the data distribution. We design private algorithms in this augmented setting for three flagship distribution testing tasks, uniformity, identity, and closeness testing, whose sample complexity smoothly scales with the claimed quality of the auxiliary information. We complement our algorithms with information-theoretic lower bounds, showing that their sample complexity is optimal (up to logarithmic factors).

Privacy in Metalearning and Multitask Learning: Modeling and Separations

Model personalization allows a set of individuals, each facing a different learning task, to train models that are more accurate for each person than those they could develop individually. The goals of personalization are captured in a variety of formal frameworks, such as multitask learning and metalearning. Combining data for model personalization poses risks for privacy because the output of an individual's model can depend on the data of other individuals. In this work we undertake a systematic study of differentially private personalized learning. Our first main contribution is to construct a taxonomy of formal frameworks for private personalized learning. This taxonomy captures different formal frameworks for learning as well as different threat models for the attacker. Our second main contribution is to prove separations between the personalized learning problems corresponding to different choices. In particular, we prove a novel separation between private multitask learning and private metalearning.

Optimal Algorithms for Augmented Testing of Discrete Distributions

We consider the problem of hypothesis testing for discrete distributions. In the standard model, where we have sample access to an underlying distribution $p$, extensive research has established optimal bounds for uniformity testing, identity testing (goodness of fit), and closeness testing (equivalence or two-sample testing). We explore these problems in a setting where a predicted data distribution, possibly derived from historical data or predictive machine learning models, is available. We demonstrate that such a predictor can indeed reduce the number of samples required for all three property testing tasks. The reduction in sample complexity depends directly on the predictor's quality, measured by its total variation distance from $p$. A key advantage of our algorithms is their adaptability to the precision of the prediction. Specifically, our algorithms can self-adjust their sample complexity based on the accuracy of the available prediction, operating without any prior knowledge of the estimation's accuracy (i.e. they are consistent). Additionally, we never use more samples than the standard approaches require, even if the predictions provide no meaningful information (i.e. they are also robust). We provide lower bounds to indicate that the improvements in sample complexity achieved by our algorithms are information-theoretically optimal. Furthermore, experimental results show that the performance of our algorithms on real data significantly exceeds our worst-case guarantees for sample complexity, demonstrating the practicality of our approach.

Enhancing Feature-Specific Data Protection via Bayesian Coordinate Differential Privacy

Local Differential Privacy (LDP) offers strong privacy guarantees without requiring users to trust external parties. However, LDP applies uniform protection to all data features, including less sensitive ones, which degrades performance of downstream tasks. To overcome this limitation, we propose a Bayesian framework, Bayesian Coordinate Differential Privacy (BCDP), that enables feature-specific privacy quantification. This more nuanced approach complements LDP by adjusting privacy protection according to the sensitivity of each feature, enabling improved performance of downstream tasks without compromising privacy. We characterize the properties of BCDP and articulate its connections with standard non-Bayesian privacy frameworks. We further apply our BCDP framework to the problems of private mean estimation and ordinary least-squares regression. The BCDP-based approach obtains improved accuracy compared to a purely LDP-based approach, without compromising on privacy.

Metalearning with Very Few Samples Per Task

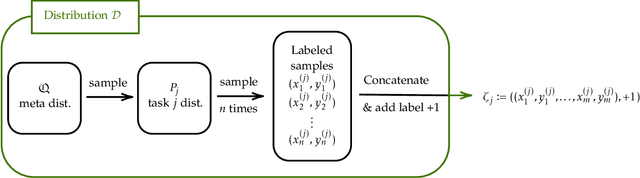
Metalearning and multitask learning are two frameworks for solving a group of related learning tasks more efficiently than we could hope to solve each of the individual tasks on their own. In multitask learning, we are given a fixed set of related learning tasks and need to output one accurate model per task, whereas in metalearning we are given tasks that are drawn i.i.d. from a metadistribution and need to output some common information that can be easily specialized to new, previously unseen tasks from the metadistribution. In this work, we consider a binary classification setting where tasks are related by a shared representation, that is, every task $P$ of interest can be solved by a classifier of the form $f_{P} \circ h$ where $h \in H$ is a map from features to some representation space that is shared across tasks, and $f_{P} \in F$ is a task-specific classifier from the representation space to labels. The main question we ask in this work is how much data do we need to metalearn a good representation? Here, the amount of data is measured in terms of both the number of tasks $t$ that we need to see and the number of samples $n$ per task. We focus on the regime where the number of samples per task is extremely small. Our main result shows that, in a distribution-free setting where the feature vectors are in $\mathbb{R}^d$, the representation is a linear map from $\mathbb{R}^d \to \mathbb{R}^k$, and the task-specific classifiers are halfspaces in $\mathbb{R}^k$, we can metalearn a representation with error $\varepsilon$ using just $n = k+2$ samples per task, and $d \cdot (1/\varepsilon)^{O(k)}$ tasks. Learning with so few samples per task is remarkable because metalearning would be impossible with $k+1$ samples per task, and because we cannot even hope to learn an accurate task-specific classifier with just $k+2$ samples per task.

Differentially Private Medians and Interior Points for Non-Pathological Data

We construct differentially private estimators with low sample complexity that estimate the median of an arbitrary distribution over $\mathbb{R}$ satisfying very mild moment conditions. Our result stands in contrast to the surprising negative result of Bun et al. (FOCS 2015) that showed there is no differentially private estimator with any finite sample complexity that returns any non-trivial approximation to the median of an arbitrary distribution.