Robust Estimation Under Heterogeneous Corruption Rates

We study the problem of robust estimation under heterogeneous corruption rates, where each sample may be independently corrupted with a known but non-identical probability. This setting arises naturally in distributed and federated learning, crowdsourcing, and sensor networks, yet existing robust estimators typically assume uniform or worst-case corruption, ignoring structural heterogeneity. For mean estimation for multivariate bounded distributions and univariate gaussian distributions, we give tight minimax rates for all heterogeneous corruption patterns. For multivariate gaussian mean estimation and linear regression, we establish the minimax rate for squared error up to a factor of $\sqrt{d}$, where $d$ is the dimension. Roughly, our findings suggest that samples beyond a certain corruption threshold may be discarded by the optimal estimators -- this threshold is determined by the empirical distribution of the corruption rates given.

Online Assortment and Price Optimization Under Contextual Choice Models

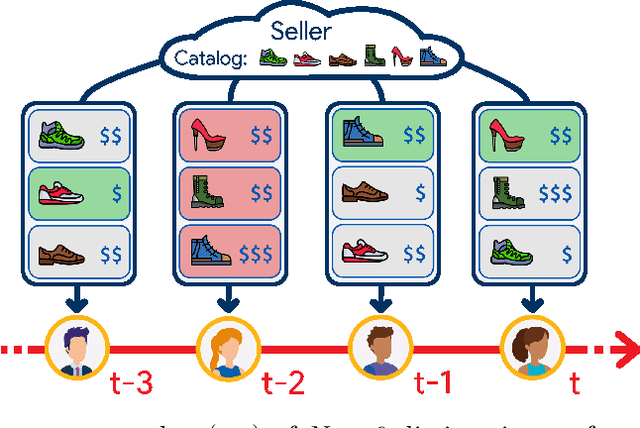
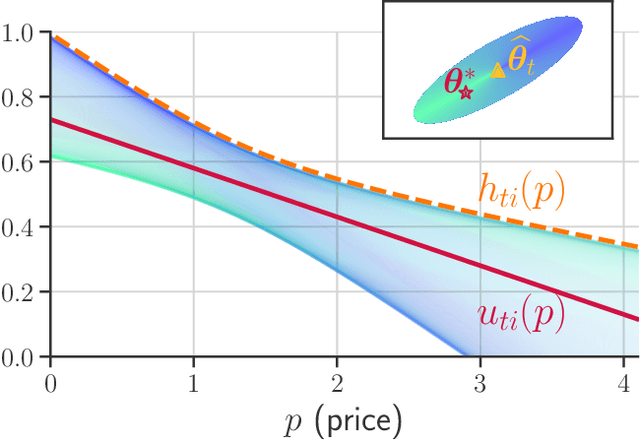
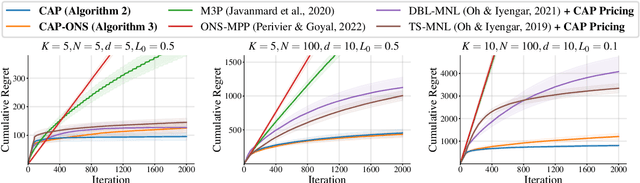
We consider an assortment selection and pricing problem in which a seller has $N$ different items available for sale. In each round, the seller observes a $d$-dimensional contextual preference information vector for the user, and offers to the user an assortment of $K$ items at prices chosen by the seller. The user selects at most one of the products from the offered assortment according to a multinomial logit choice model whose parameters are unknown. The seller observes which, if any, item is chosen at the end of each round, with the goal of maximizing cumulative revenue over a selling horizon of length $T$. For this problem, we propose an algorithm that learns from user feedback and achieves a revenue regret of order $\widetilde{O}(d \sqrt{K T} / L_0 )$ where $L_0$ is the minimum price sensitivity parameter. We also obtain a lower bound of order $\Omega(d \sqrt{T}/ L_0)$ for the regret achievable by any algorithm.

Enhancing Feature-Specific Data Protection via Bayesian Coordinate Differential Privacy

Local Differential Privacy (LDP) offers strong privacy guarantees without requiring users to trust external parties. However, LDP applies uniform protection to all data features, including less sensitive ones, which degrades performance of downstream tasks. To overcome this limitation, we propose a Bayesian framework, Bayesian Coordinate Differential Privacy (BCDP), that enables feature-specific privacy quantification. This more nuanced approach complements LDP by adjusting privacy protection according to the sensitivity of each feature, enabling improved performance of downstream tasks without compromising privacy. We characterize the properties of BCDP and articulate its connections with standard non-Bayesian privacy frameworks. We further apply our BCDP framework to the problems of private mean estimation and ordinary least-squares regression. The BCDP-based approach obtains improved accuracy compared to a purely LDP-based approach, without compromising on privacy.

Empirical Mean and Frequency Estimation Under Heterogeneous Privacy: A Worst-Case Analysis

Differential Privacy (DP) is the current gold-standard for measuring privacy. Estimation problems under DP constraints appearing in the literature have largely focused on providing equal privacy to all users. We consider the problems of empirical mean estimation for univariate data and frequency estimation for categorical data, two pillars of data analysis in the industry, subject to heterogeneous privacy constraints. Each user, contributing a sample to the dataset, is allowed to have a different privacy demand. The dataset itself is assumed to be worst-case and we study both the problems in two different formulations -- the correlated and the uncorrelated setting. In the former setting, the privacy demand and the user data can be arbitrarily correlated while in the latter setting, there is no correlation between the dataset and the privacy demand. We prove some optimality results, under both PAC error and mean-squared error, for our proposed algorithms and demonstrate superior performance over other baseline techniques experimentally.

Mean Estimation Under Heterogeneous Privacy Demands

Differential Privacy (DP) is a well-established framework to quantify privacy loss incurred by any algorithm. Traditional formulations impose a uniform privacy requirement for all users, which is often inconsistent with real-world scenarios in which users dictate their privacy preferences individually. This work considers the problem of mean estimation, where each user can impose their own distinct privacy level. The algorithm we propose is shown to be minimax optimal and has a near-linear run-time. Our results elicit an interesting saturation phenomenon that occurs. Namely, the privacy requirements of the most stringent users dictate the overall error rates. As a consequence, users with less but differing privacy requirements are all given more privacy than they require, in equal amounts. In other words, these privacy-indifferent users are given a nontrivial degree of privacy for free, without any sacrifice in the performance of the estimator.

Worst-case vs Average-case Design for Estimation from Fixed Pairwise Comparisons

Pairwise comparison data arises in many domains, including tournament rankings, web search, and preference elicitation. Given noisy comparisons of a fixed subset of pairs of items, we study the problem of estimating the underlying comparison probabilities under the assumption of strong stochastic transitivity (SST). We also consider the noisy sorting subclass of the SST model. We show that when the assignment of items to the topology is arbitrary, these permutation-based models, unlike their parametric counterparts, do not admit consistent estimation for most comparison topologies used in practice. We then demonstrate that consistent estimation is possible when the assignment of items to the topology is randomized, thus establishing a dichotomy between worst-case and average-case designs. We propose two estimators in the average-case setting and analyze their risk, showing that it depends on the comparison topology only through the degree sequence of the topology. The rates achieved by these estimators are shown to be optimal for a large class of graphs. Our results are corroborated by simulations on multiple comparison topologies.

Denoising Linear Models with Permuted Data

The multivariate linear regression model with shuffled data and additive Gaussian noise arises in various correspondence estimation and matching problems. Focusing on the denoising aspect of this problem, we provide a characterization the minimax error rate that is sharp up to logarithmic factors. We also analyze the performance of two versions of a computationally efficient estimator, and establish their consistency for a large range of input parameters. Finally, we provide an exact algorithm for the noiseless problem and demonstrate its performance on an image point-cloud matching task. Our analysis also extends to datasets with outliers.

Linear Regression with an Unknown Permutation: Statistical and Computational Limits

Consider a noisy linear observation model with an unknown permutation, based on observing $y = \Pi^* A x^* + w$, where $x^* \in \mathbb{R}^d$ is an unknown vector, $\Pi^*$ is an unknown $n \times n$ permutation matrix, and $w \in \mathbb{R}^n$ is additive Gaussian noise. We analyze the problem of permutation recovery in a random design setting in which the entries of the matrix $A$ are drawn i.i.d. from a standard Gaussian distribution, and establish sharp conditions on the SNR, sample size $n$, and dimension $d$ under which $\Pi^*$ is exactly and approximately recoverable. On the computational front, we show that the maximum likelihood estimate of $\Pi^*$ is NP-hard to compute, while also providing a polynomial time algorithm when $d =1$.