Sharp Results for Hypothesis Testing with Risk-Sensitive Agents

Statistical protocols are often used for decision-making involving multiple parties, each with their own incentives, private information, and ability to influence the distributional properties of the data. We study a game-theoretic version of hypothesis testing in which a statistician, also known as a principal, interacts with strategic agents that can generate data. The statistician seeks to design a testing protocol with controlled error, while the data-generating agents, guided by their utility and prior information, choose whether or not to opt in based on expected utility maximization. This strategic behavior affects the data observed by the statistician and, consequently, the associated testing error. We analyze this problem for general concave and monotonic utility functions and prove an upper bound on the Bayes false discovery rate (FDR). Underlying this bound is a form of prior elicitation: we show how an agent's choice to opt in implies a certain upper bound on their prior null probability. Our FDR bound is unimprovable in a strong sense, achieving equality at a single point for an individual agent and at any countable number of points for a population of agents. We also demonstrate that our testing protocols exhibit a desirable maximin property when the principal's utility is considered. To illustrate the qualitative predictions of our theory, we examine the effects of risk aversion, reward stochasticity, and signal-to-noise ratio, as well as the implications for the Food and Drug Administration's testing protocols.

Exploiting Exogenous Structure for Sample-Efficient Reinforcement Learning

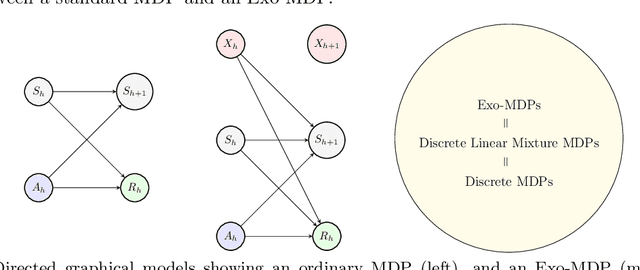
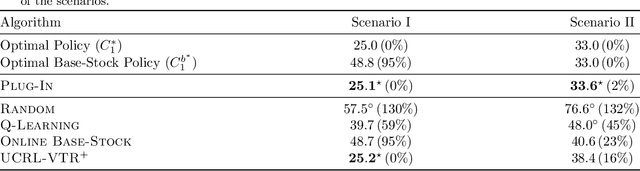
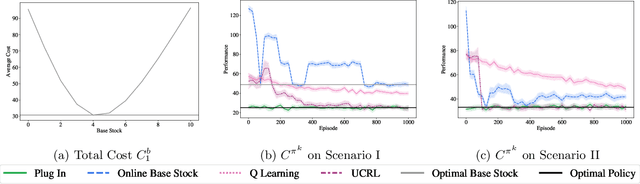
We study a class of structured Markov Decision Processes (MDPs) known as Exo-MDPs, characterized by a partition of the state space into two components. The exogenous states evolve stochastically in a manner not affected by the agent's actions, whereas the endogenous states are affected by the actions, and evolve in a deterministic and known way conditional on the exogenous states. Exo-MDPs are a natural model for various applications including inventory control, finance, power systems, ride sharing, among others. Despite seeming restrictive, this work establishes that any discrete MDP can be represented as an Exo-MDP. Further, Exo-MDPs induce a natural representation of the transition and reward dynamics as linear functions of the exogenous state distribution. This linear representation leads to near-optimal algorithms with regret guarantees scaling only with the (effective) size of the exogenous state space $d$, independent of the sizes of the endogenous state and action spaces. Specifically, when the exogenous state is fully observed, a simple plug-in approach achieves a regret upper bound of $O(H^{3/2}\sqrt{dK})$, where $H$ denotes the horizon and $K$ denotes the total number of episodes. When the exogenous state is unobserved, the linear representation leads to a regret upper bound of $O(H^{3/2}d\sqrt{K})$. We also establish a nearly matching regret lower bound of $\Omega(Hd\sqrt{K})$ for the no observation regime. We complement our theoretical findings with an experimental study on inventory control problems.

Finite-Sample Guarantees for Best-Response Learning Dynamics in Zero-Sum Matrix Games

We study best-response type learning dynamics for two player zero-sum matrix games. We consider two settings that are distinguished by the type of information that each player has about the game and their opponent's strategy. The first setting is the full information case, in which each player knows their own and the opponent's payoff matrices and observes the opponent's mixed strategy. The second setting is the minimal information case, where players do not observe the opponent's strategy and are not aware of either of the payoff matrices (instead they only observe their realized payoffs). For this setting, also known as the radically uncoupled case in the learning in games literature, we study a two-timescale learning dynamics that combine smoothed best-response type updates for strategy estimates with a TD-learning update to estimate a local payoff function. For these dynamics, without additional exploration, we provide polynomial-time finite-sample guarantees for convergence to an $\epsilon$-Nash equilibrium.

Entrywise Inference for Causal Panel Data: A Simple and Instance-Optimal Approach

In causal inference with panel data under staggered adoption, the goal is to estimate and derive confidence intervals for potential outcomes and treatment effects. We propose a computationally efficient procedure, involving only simple matrix algebra and singular value decomposition. We derive non-asymptotic bounds on the entrywise error, establishing its proximity to a suitably scaled Gaussian variable. Despite its simplicity, our procedure turns out to be instance-optimal, in that our theoretical scaling matches a local instance-wise lower bound derived via a Bayesian Cram\'{e}r-Rao argument. Using our insights, we develop a data-driven procedure for constructing entrywise confidence intervals with pre-specified coverage guarantees. Our analysis is based on a general inferential toolbox for the SVD algorithm applied to the matrix denoising model, which might be of independent interest.

Taming "data-hungry" reinforcement learning? Stability in continuous state-action spaces

We introduce a novel framework for analyzing reinforcement learning (RL) in continuous state-action spaces, and use it to prove fast rates of convergence in both off-line and on-line settings. Our analysis highlights two key stability properties, relating to how changes in value functions and/or policies affect the Bellman operator and occupation measures. We argue that these properties are satisfied in many continuous state-action Markov decision processes, and demonstrate how they arise naturally when using linear function approximation methods. Our analysis offers fresh perspectives on the roles of pessimism and optimism in off-line and on-line RL, and highlights the connection between off-line RL and transfer learning.

Doubly High-Dimensional Contextual Bandits: An Interpretable Model for Joint Assortment-Pricing

Key challenges in running a retail business include how to select products to present to consumers (the assortment problem), and how to price products (the pricing problem) to maximize revenue or profit. Instead of considering these problems in isolation, we propose a joint approach to assortment-pricing based on contextual bandits. Our model is doubly high-dimensional, in that both context vectors and actions are allowed to take values in high-dimensional spaces. In order to circumvent the curse of dimensionality, we propose a simple yet flexible model that captures the interactions between covariates and actions via a (near) low-rank representation matrix. The resulting class of models is reasonably expressive while remaining interpretable through latent factors, and includes various structured linear bandit and pricing models as particular cases. We propose a computationally tractable procedure that combines an exploration/exploitation protocol with an efficient low-rank matrix estimator, and we prove bounds on its regret. Simulation results show that this method has lower regret than state-of-the-art methods applied to various standard bandit and pricing models. Real-world case studies on the assortment-pricing problem, from an industry-leading instant noodles company to an emerging beauty start-up, underscore the gains achievable using our method. In each case, we show at least three-fold gains in revenue or profit by our bandit method, as well as the interpretability of the latent factor models that are learned.

Semi-parametric inference based on adaptively collected data

Many standard estimators, when applied to adaptively collected data, fail to be asymptotically normal, thereby complicating the construction of confidence intervals. We address this challenge in a semi-parametric context: estimating the parameter vector of a generalized linear regression model contaminated by a non-parametric nuisance component. We construct suitably weighted estimating equations that account for adaptivity in data collection, and provide conditions under which the associated estimates are asymptotically normal. Our results characterize the degree of "explorability" required for asymptotic normality to hold. For the simpler problem of estimating a linear functional, we provide similar guarantees under much weaker assumptions. We illustrate our general theory with concrete consequences for various problems, including standard linear bandits and sparse generalized bandits, and compare with other methods via simulation studies.

Kernel-based off-policy estimation without overlap: Instance optimality beyond semiparametric efficiency

We study optimal procedures for estimating a linear functional based on observational data. In many problems of this kind, a widely used assumption is strict overlap, i.e., uniform boundedness of the importance ratio, which measures how well the observational data covers the directions of interest. When it is violated, the classical semi-parametric efficiency bound can easily become infinite, so that the instance-optimal risk depends on the function class used to model the regression function. For any convex and symmetric function class $\mathcal{F}$, we derive a non-asymptotic local minimax bound on the mean-squared error in estimating a broad class of linear functionals. This lower bound refines the classical semi-parametric one, and makes connections to moduli of continuity in functional estimation. When $\mathcal{F}$ is a reproducing kernel Hilbert space, we prove that this lower bound can be achieved up to a constant factor by analyzing a computationally simple regression estimator. We apply our general results to various families of examples, thereby uncovering a spectrum of rates that interpolate between the classical theories of semi-parametric efficiency (with $\sqrt{n}$-consistency) and the slower minimax rates associated with non-parametric function estimation.

Policy evaluation from a single path: Multi-step methods, mixing and mis-specification

We study non-parametric estimation of the value function of an infinite-horizon $\gamma$-discounted Markov reward process (MRP) using observations from a single trajectory. We provide non-asymptotic guarantees for a general family of kernel-based multi-step temporal difference (TD) estimates, including canonical $K$-step look-ahead TD for $K = 1, 2, \ldots$ and the TD$(\lambda)$ family for $\lambda \in [0,1)$ as special cases. Our bounds capture its dependence on Bellman fluctuations, mixing time of the Markov chain, any mis-specification in the model, as well as the choice of weight function defining the estimator itself, and reveal some delicate interactions between mixing time and model mis-specification. For a given TD method applied to a well-specified model, its statistical error under trajectory data is similar to that of i.i.d. sample transition pairs, whereas under mis-specification, temporal dependence in data inflates the statistical error. However, any such deterioration can be mitigated by increased look-ahead. We complement our upper bounds by proving minimax lower bounds that establish optimality of TD-based methods with appropriately chosen look-ahead and weighting, and reveal some fundamental differences between value function estimation and ordinary non-parametric regression.

Krylov-Bellman boosting: Super-linear policy evaluation in general state spaces

We present and analyze the Krylov-Bellman Boosting (KBB) algorithm for policy evaluation in general state spaces. It alternates between fitting the Bellman residual using non-parametric regression (as in boosting), and estimating the value function via the least-squares temporal difference (LSTD) procedure applied with a feature set that grows adaptively over time. By exploiting the connection to Krylov methods, we equip this method with two attractive guarantees. First, we provide a general convergence bound that allows for separate estimation errors in residual fitting and LSTD computation. Consistent with our numerical experiments, this bound shows that convergence rates depend on the restricted spectral structure, and are typically super-linear. Second, by combining this meta-result with sample-size dependent guarantees for residual fitting and LSTD computation, we obtain concrete statistical guarantees that depend on the sample size along with the complexity of the function class used to fit the residuals. We illustrate the behavior of the KBB algorithm for various types of policy evaluation problems, and typically find large reductions in sample complexity relative to the standard approach of fitted value iterationn.