Minimax Optimal Convergence of Gradient Descent in Logistic Regression via Large and Adaptive Stepsizes

We study $\textit{gradient descent}$ (GD) for logistic regression on linearly separable data with stepsizes that adapt to the current risk, scaled by a constant hyperparameter $\eta$. We show that after at most $1/\gamma^2$ burn-in steps, GD achieves a risk upper bounded by $\exp(-\Theta(\eta))$, where $\gamma$ is the margin of the dataset. As $\eta$ can be arbitrarily large, GD attains an arbitrarily small risk $\textit{immediately after the burn-in steps}$, though the risk evolution may be $\textit{non-monotonic}$. We further construct hard datasets with margin $\gamma$, where any batch or online first-order method requires $\Omega(1/\gamma^2)$ steps to find a linear separator. Thus, GD with large, adaptive stepsizes is $\textit{minimax optimal}$ among first-order batch methods. Notably, the classical $\textit{Perceptron}$ (Novikoff, 1962), a first-order online method, also achieves a step complexity of $1/\gamma^2$, matching GD even in constants. Finally, our GD analysis extends to a broad class of loss functions and certain two-layer networks.

Improving LLM Safety Alignment with Dual-Objective Optimization

Existing training-time safety alignment techniques for large language models (LLMs) remain vulnerable to jailbreak attacks. Direct preference optimization (DPO), a widely deployed alignment method, exhibits limitations in both experimental and theoretical contexts as its loss function proves suboptimal for refusal learning. Through gradient-based analysis, we identify these shortcomings and propose an improved safety alignment that disentangles DPO objectives into two components: (1) robust refusal training, which encourages refusal even when partial unsafe generations are produced, and (2) targeted unlearning of harmful knowledge. This approach significantly increases LLM robustness against a wide range of jailbreak attacks, including prefilling, suffix, and multi-turn attacks across both in-distribution and out-of-distribution scenarios. Furthermore, we introduce a method to emphasize critical refusal tokens by incorporating a reward-based token-level weighting mechanism for refusal learning, which further improves the robustness against adversarial exploits. Our research also suggests that robustness to jailbreak attacks is correlated with token distribution shifts in the training process and internal representations of refusal and harmful tokens, offering valuable directions for future research in LLM safety alignment. The code is available at https://github.com/wicai24/DOOR-Alignment

A Statistical Theory of Contrastive Pre-training and Multimodal Generative AI

Multi-modal generative AI systems, such as those combining vision and language, rely on contrastive pre-training to learn representations across different modalities. While their practical benefits are widely acknowledged, a rigorous theoretical understanding of the contrastive pre-training framework remains limited. This paper develops a theoretical framework to explain the success of contrastive pre-training in downstream tasks, such as zero-shot classification, conditional diffusion models, and vision-language models. We introduce the concept of approximate sufficient statistics, a generalization of the classical sufficient statistics, and show that near-minimizers of the contrastive pre-training loss are approximately sufficient, making them adaptable to diverse downstream tasks. We further propose the Joint Generative Hierarchical Model for the joint distribution of images and text, showing that transformers can efficiently approximate relevant functions within this model via belief propagation. Building on this framework, we derive sample complexity guarantees for multi-modal learning based on contrastive pre-trained representations. Numerical simulations validate these theoretical findings, demonstrating the strong generalization performance of contrastively pre-trained transformers in various multi-modal tasks.

Simplicity Prevails: Rethinking Negative Preference Optimization for LLM Unlearning

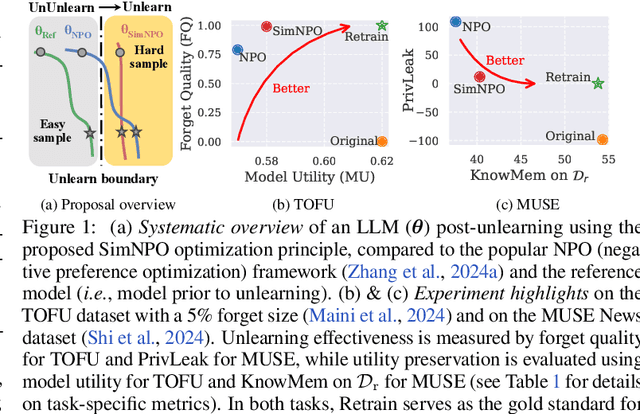
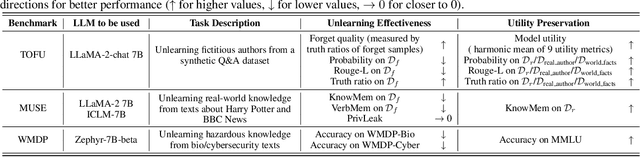
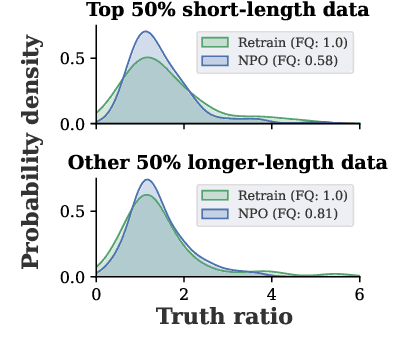
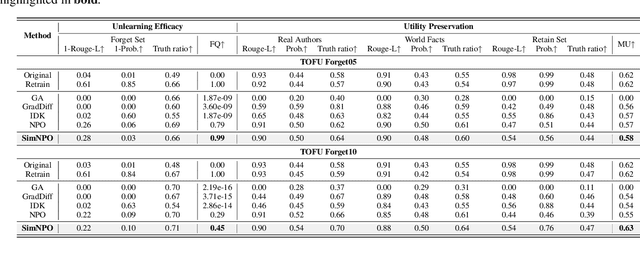
In this work, we address the problem of large language model (LLM) unlearning, aiming to remove unwanted data influences and associated model capabilities (e.g., copyrighted data or harmful content generation) while preserving essential model utilities, without the need for retraining from scratch. Despite the growing need for LLM unlearning, a principled optimization framework remains lacking. To this end, we revisit the state-of-the-art approach, negative preference optimization (NPO), and identify the issue of reference model bias, which could undermine NPO's effectiveness, particularly when unlearning forget data of varying difficulty. Given that, we propose a simple yet effective unlearning optimization framework, called SimNPO, showing that 'simplicity' in removing the reliance on a reference model (through the lens of simple preference optimization) benefits unlearning. We also provide deeper insights into SimNPO's advantages, supported by analysis using mixtures of Markov chains. Furthermore, we present extensive experiments validating SimNPO's superiority over existing unlearning baselines in benchmarks like TOFU and MUSE, and robustness against relearning attacks. Codes are available at https://github.com/OPTML-Group/Unlearn-Simple.

Scaling Laws in Linear Regression: Compute, Parameters, and Data

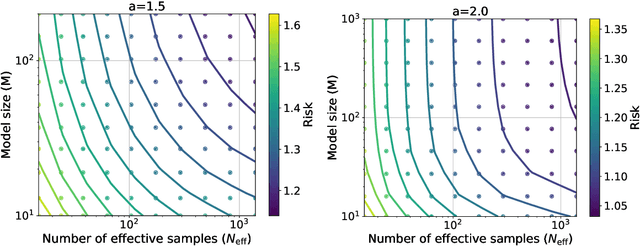
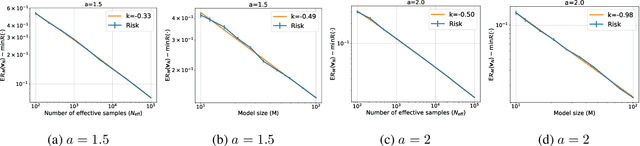
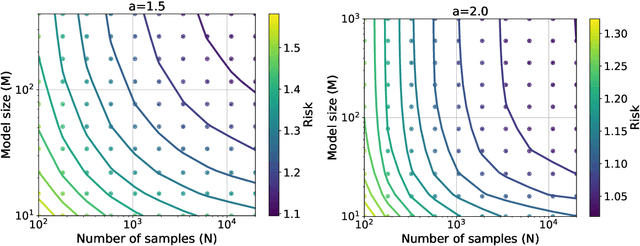
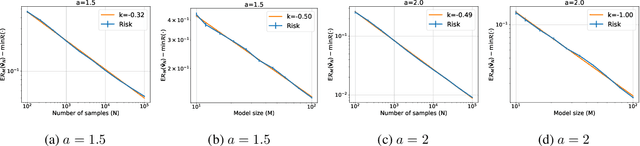
Empirically, large-scale deep learning models often satisfy a neural scaling law: the test error of the trained model improves polynomially as the model size and data size grow. However, conventional wisdom suggests the test error consists of approximation, bias, and variance errors, where the variance error increases with model size. This disagrees with the general form of neural scaling laws, which predict that increasing model size monotonically improves performance. We study the theory of scaling laws in an infinite dimensional linear regression setup. Specifically, we consider a model with $M$ parameters as a linear function of sketched covariates. The model is trained by one-pass stochastic gradient descent (SGD) using $N$ data. Assuming the optimal parameter satisfies a Gaussian prior and the data covariance matrix has a power-law spectrum of degree $a>1$, we show that the reducible part of the test error is $\Theta(M^{-(a-1)} + N^{-(a-1)/a})$. The variance error, which increases with $M$, is dominated by the other errors due to the implicit regularization of SGD, thus disappearing from the bound. Our theory is consistent with the empirical neural scaling laws and verified by numerical simulation.

Negative Preference Optimization: From Catastrophic Collapse to Effective Unlearning

Large Language Models (LLMs) often memorize sensitive, private, or copyrighted data during pre-training. LLM unlearning aims to eliminate the influence of undesirable data from the pre-trained model while preserving the model's utilities on other tasks. Several practical methods have recently been proposed for LLM unlearning, mostly based on gradient ascent (GA) on the loss of undesirable data. However, on certain unlearning tasks, these methods either fail to effectively unlearn the target data or suffer from catastrophic collapse -- a drastic degradation of the model's utilities. In this paper, we propose Negative Preference Optimization (NPO), a simple alignment-inspired method that could efficiently and effectively unlearn a target dataset. We theoretically show that the progression toward catastrophic collapse by minimizing the NPO loss is exponentially slower than GA. Through experiments on synthetic data and the benchmark TOFU dataset, we demonstrate that NPO-based methods achieve a better balance between unlearning the undesirable data and maintaining the model's utilities. We also observe that NPO-based methods generate more sensible outputs than GA-based methods, whose outputs are often gibberish. Remarkably, on TOFU, NPO-based methods are the first to achieve reasonable unlearning results in forgetting 50% (or more) of the training data, whereas existing methods already struggle with forgetting 10% of training data.

Mean-field variational inference with the TAP free energy: Geometric and statistical properties in linear models

We study mean-field variational inference in a Bayesian linear model when the sample size n is comparable to the dimension p. In high dimensions, the common approach of minimizing a Kullback-Leibler divergence from the posterior distribution, or maximizing an evidence lower bound, may deviate from the true posterior mean and underestimate posterior uncertainty. We study instead minimization of the TAP free energy, showing in a high-dimensional asymptotic framework that it has a local minimizer which provides a consistent estimate of the posterior marginals and may be used for correctly calibrated posterior inference. Geometrically, we show that the landscape of the TAP free energy is strongly convex in an extensive neighborhood of this local minimizer, which under certain general conditions can be found by an Approximate Message Passing (AMP) algorithm. We then exhibit an efficient algorithm that linearly converges to the minimizer within this local neighborhood. In settings where it is conjectured that no efficient algorithm can find this local neighborhood, we prove analogous geometric properties for a local minimizer of the TAP free energy reachable by AMP, and show that posterior inference based on this minimizer remains correctly calibrated.

Transformers as Decision Makers: Provable In-Context Reinforcement Learning via Supervised Pretraining

Large transformer models pretrained on offline reinforcement learning datasets have demonstrated remarkable in-context reinforcement learning (ICRL) capabilities, where they can make good decisions when prompted with interaction trajectories from unseen environments. However, when and how transformers can be trained to perform ICRL have not been theoretically well-understood. In particular, it is unclear which reinforcement-learning algorithms transformers can perform in context, and how distribution mismatch in offline training data affects the learned algorithms. This paper provides a theoretical framework that analyzes supervised pretraining for ICRL. This includes two recently proposed training methods -- algorithm distillation and decision-pretrained transformers. First, assuming model realizability, we prove the supervised-pretrained transformer will imitate the conditional expectation of the expert algorithm given the observed trajectory. The generalization error will scale with model capacity and a distribution divergence factor between the expert and offline algorithms. Second, we show transformers with ReLU attention can efficiently approximate near-optimal online reinforcement learning algorithms like LinUCB and Thompson sampling for stochastic linear bandits, and UCB-VI for tabular Markov decision processes. This provides the first quantitative analysis of the ICRL capabilities of transformers pretrained from offline trajectories.

Statistical Limits of Adaptive Linear Models: Low-Dimensional Estimation and Inference

Estimation and inference in statistics pose significant challenges when data are collected adaptively. Even in linear models, the Ordinary Least Squares (OLS) estimator may fail to exhibit asymptotic normality for single coordinate estimation and have inflated error. This issue is highlighted by a recent minimax lower bound, which shows that the error of estimating a single coordinate can be enlarged by a multiple of $\sqrt{d}$ when data are allowed to be arbitrarily adaptive, compared with the case when they are i.i.d. Our work explores this striking difference in estimation performance between utilizing i.i.d. and adaptive data. We investigate how the degree of adaptivity in data collection impacts the performance of estimating a low-dimensional parameter component in high-dimensional linear models. We identify conditions on the data collection mechanism under which the estimation error for a low-dimensional parameter component matches its counterpart in the i.i.d. setting, up to a factor that depends on the degree of adaptivity. We show that OLS or OLS on centered data can achieve this matching error. In addition, we propose a novel estimator for single coordinate inference via solving a Two-stage Adaptive Linear Estimating equation (TALE). Under a weaker form of adaptivity in data collection, we establish an asymptotic normality property of the proposed estimator.

Plug-in Performative Optimization

When predictions are performative, the choice of which predictor to deploy influences the distribution of future observations. The overarching goal in learning under performativity is to find a predictor that has low \emph{performative risk}, that is, good performance on its induced distribution. One family of solutions for optimizing the performative risk, including bandits and other derivative-free methods, is agnostic to any structure in the performative feedback, leading to exceedingly slow convergence rates. A complementary family of solutions makes use of explicit \emph{models} for the feedback, such as best-response models in strategic classification, enabling significantly faster rates. However, these rates critically rely on the feedback model being well-specified. In this work we initiate a study of the use of possibly \emph{misspecified} models in performative prediction. We study a general protocol for making use of models, called \emph{plug-in performative optimization}, and prove bounds on its excess risk. We show that plug-in performative optimization can be far more efficient than model-agnostic strategies, as long as the misspecification is not too extreme. Altogether, our results support the hypothesis that models--even if misspecified--can indeed help with learning in performative settings.