UCB algorithms for multi-armed bandits: Precise regret and adaptive inference

Upper Confidence Bound (UCB) algorithms are a widely-used class of sequential algorithms for the $K$-armed bandit problem. Despite extensive research over the past decades aimed at understanding their asymptotic and (near) minimax optimality properties, a precise understanding of their regret behavior remains elusive. This gap has not only hindered the evaluation of their actual algorithmic efficiency, but also limited further developments in statistical inference in sequential data collection. This paper bridges these two fundamental aspects--precise regret analysis and adaptive statistical inference--through a deterministic characterization of the number of arm pulls for an UCB index algorithm [Lai87, Agr95, ACBF02]. Our resulting precise regret formula not only accurately captures the actual behavior of the UCB algorithm for finite time horizons and individual problem instances, but also provides significant new insights into the regimes in which the existing theory remains informative. In particular, we show that the classical Lai-Robbins regret formula is exact if and only if the sub-optimality gaps exceed the order $\sigma\sqrt{K\log T/T}$. We also show that its maximal regret deviates from the minimax regret by a logarithmic factor, and therefore settling its strict minimax optimality in the negative. The deterministic characterization of the number of arm pulls for the UCB algorithm also has major implications in adaptive statistical inference. Building on the seminal work of [Lai82], we show that the UCB algorithm satisfies certain stability properties that lead to quantitative central limit theorems in two settings including the empirical means of unknown rewards in the bandit setting. These results have an important practical implication: conventional confidence sets designed for i.i.d. data remain valid even when data are collected sequentially.

On Lai's Upper Confidence Bound in Multi-Armed Bandits

In this memorial paper, we honor Tze Leung Lai's seminal contributions to the topic of multi-armed bandits, with a specific focus on his pioneering work on the upper confidence bound. We establish sharp non-asymptotic regret bounds for an upper confidence bound index with a constant level of exploration for Gaussian rewards. Furthermore, we establish a non-asymptotic regret bound for the upper confidence bound index of \cite{lai1987adaptive} which employs an exploration function that decreases with the sample size of the corresponding arm. The regret bounds have leading constants that match the Lai-Robbins lower bound. Our results highlight an aspect of Lai's seminal works that deserves more attention in the machine learning literature.

Inference with the Upper Confidence Bound Algorithm

In this paper, we discuss the asymptotic behavior of the Upper Confidence Bound (UCB) algorithm in the context of multiarmed bandit problems and discuss its implication in downstream inferential tasks. While inferential tasks become challenging when data is collected in a sequential manner, we argue that this problem can be alleviated when the sequential algorithm at hand satisfies certain stability property. This notion of stability is motivated from the seminal work of Lai and Wei (1982). Our first main result shows that such a stability property is always satisfied for the UCB algorithm, and as a result the sample means for each arm are asymptotically normal. Next, we examine the stability properties of the UCB algorithm when the number of arms $K$ is allowed to grow with the number of arm pulls $T$. We show that in such a case the arms are stable when $\frac{\log K}{\log T} \rightarrow 0$, and the number of near-optimal arms are large.

Statistical Limits of Adaptive Linear Models: Low-Dimensional Estimation and Inference

Estimation and inference in statistics pose significant challenges when data are collected adaptively. Even in linear models, the Ordinary Least Squares (OLS) estimator may fail to exhibit asymptotic normality for single coordinate estimation and have inflated error. This issue is highlighted by a recent minimax lower bound, which shows that the error of estimating a single coordinate can be enlarged by a multiple of $\sqrt{d}$ when data are allowed to be arbitrarily adaptive, compared with the case when they are i.i.d. Our work explores this striking difference in estimation performance between utilizing i.i.d. and adaptive data. We investigate how the degree of adaptivity in data collection impacts the performance of estimating a low-dimensional parameter component in high-dimensional linear models. We identify conditions on the data collection mechanism under which the estimation error for a low-dimensional parameter component matches its counterpart in the i.i.d. setting, up to a factor that depends on the degree of adaptivity. We show that OLS or OLS on centered data can achieve this matching error. In addition, we propose a novel estimator for single coordinate inference via solving a Two-stage Adaptive Linear Estimating equation (TALE). Under a weaker form of adaptivity in data collection, we establish an asymptotic normality property of the proposed estimator.

Adaptive Linear Estimating Equations

Sequential data collection has emerged as a widely adopted technique for enhancing the efficiency of data gathering processes. Despite its advantages, such data collection mechanism often introduces complexities to the statistical inference procedure. For instance, the ordinary least squares (OLS) estimator in an adaptive linear regression model can exhibit non-normal asymptotic behavior, posing challenges for accurate inference and interpretation. In this paper, we propose a general method for constructing debiased estimator which remedies this issue. It makes use of the idea of adaptive linear estimating equations, and we establish theoretical guarantees of asymptotic normality, supplemented by discussions on achieving near-optimal asymptotic variance. A salient feature of our estimator is that in the context of multi-armed bandits, our estimator retains the non-asymptotic performance of the least square estimator while obtaining asymptotic normality property. Consequently, this work helps connect two fruitful paradigms of adaptive inference: a) non-asymptotic inference using concentration inequalities and b) asymptotic inference via asymptotic normality.

Tensor Principal Component Analysis in High Dimensional CP Models

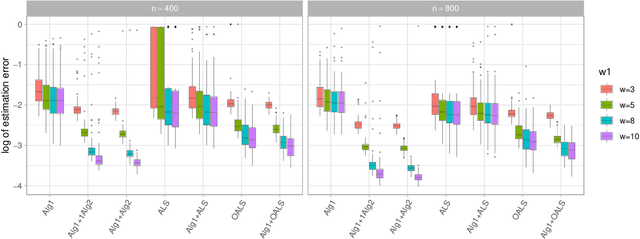
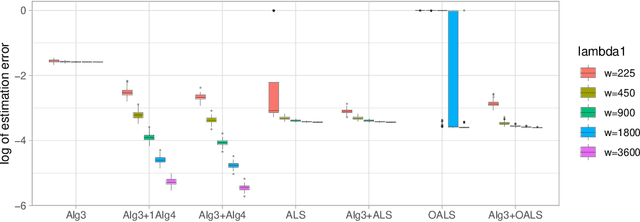
The CP decomposition for high dimensional non-orthogonal spike tensors is an important problem with broad applications across many disciplines. However, previous works with theoretical guarantee typically assume restrictive incoherence conditions on the basis vectors for the CP components. In this paper, we propose new computationally efficient composite PCA and concurrent orthogonalization algorithms for tensor CP decomposition with theoretical guarantees under mild incoherence conditions. The composite PCA applies the principal component or singular value decompositions twice, first to a matrix unfolding of the tensor data to obtain singular vectors and then to the matrix folding of the singular vectors obtained in the first step. It can be used as an initialization for any iterative optimization schemes for the tensor CP decomposition. The concurrent orthogonalization algorithm iteratively estimates the basis vector in each mode of the tensor by simultaneously applying projections to the orthogonal complements of the spaces generated by others CP components in other modes. It is designed to improve the alternating least squares estimator and other forms of the high order orthogonal iteration for tensors with low or moderately high CP ranks. Our theoretical investigation provides estimation accuracy and statistical convergence rates for the two proposed algorithms. Our implementations on synthetic data demonstrate significant practical superiority of our approach over existing methods.

Asymptotic normality of robust $M$-estimators with convex penalty

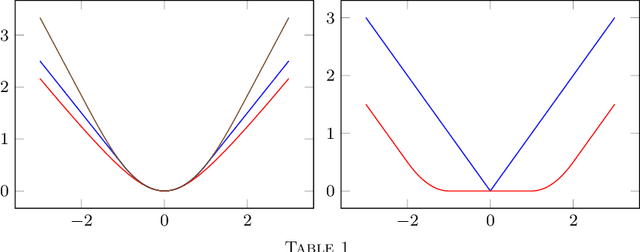
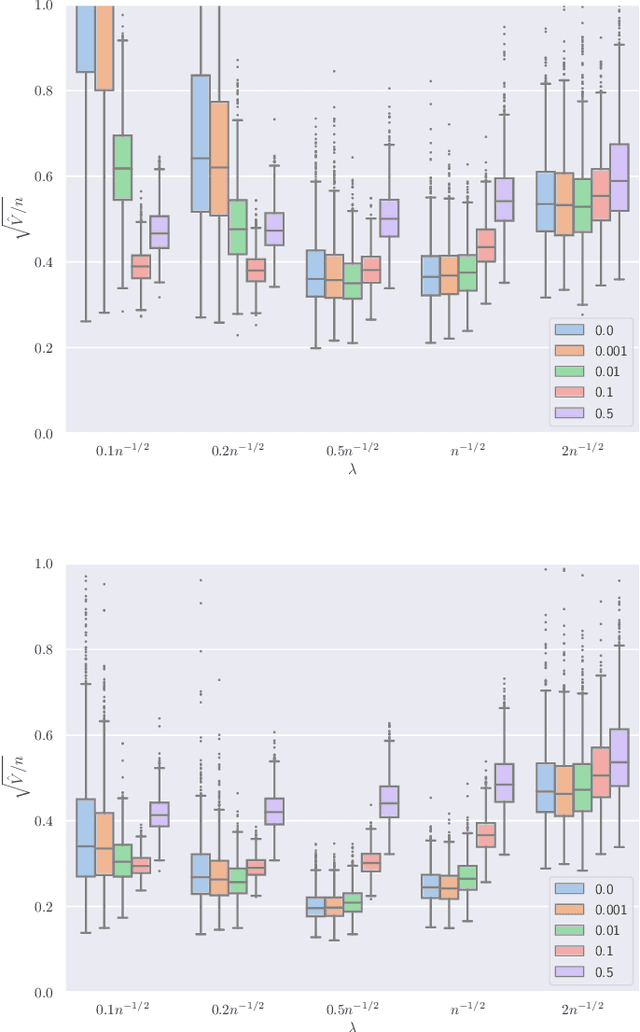
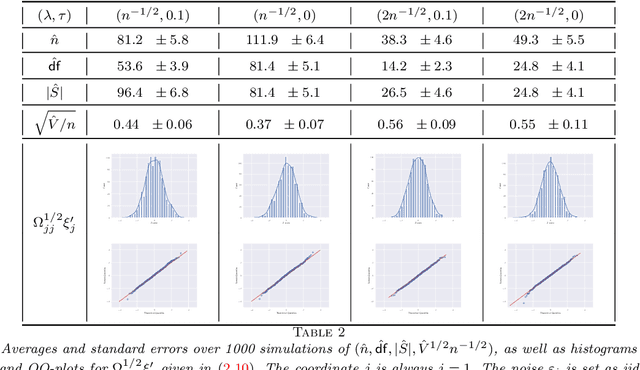
This paper develops asymptotic normality results for individual coordinates of robust M-estimators with convex penalty in high-dimensions, where the dimension $p$ is at most of the same order as the sample size $n$, i.e, $p/n\le\gamma$ for some fixed constant $\gamma>0$. The asymptotic normality requires a bias correction and holds for most coordinates of the M-estimator for a large class of loss functions including the Huber loss and its smoothed versions regularized with a strongly convex penalty. The asymptotic variance that characterizes the width of the resulting confidence intervals is estimated with data-driven quantities. This estimate of the variance adapts automatically to low ($p/n\to0)$ or high ($p/n \le \gamma$) dimensions and does not involve the proximal operators seen in previous works on asymptotic normality of M-estimators. For the Huber loss, the estimated variance has a simple expression involving an effective degrees-of-freedom as well as an effective sample size. The case of the Huber loss with Elastic-Net penalty is studied in details and a simulation study confirms the theoretical findings. The asymptotic normality results follow from Stein formulae for high-dimensional random vectors on the sphere developed in the paper which are of independent interest.

De-Biasing The Lasso With Degrees-of-Freedom Adjustment

This paper studies schemes to de-bias the Lasso in sparse linear regression where the goal is to estimate and construct confidence intervals for a low-dimensional projection of the unknown coefficient vector in a preconceived direction $a_0$. We assume that the design matrix has iid Gaussian rows with known covariance matrix $\Sigma$. Our analysis reveals that previous propositions to de-bias the Lasso require a modification in order to enjoy asymptotic efficiency in a full range of the level of sparsity. This modification takes the form of a degrees-of-freedom adjustment that accounts for the dimension of the model selected by the Lasso. Let $s_0$ denote the number of nonzero coefficients of the true coefficient vector. The unadjusted de-biasing schemes proposed in previous studies enjoys efficiency if $s_0\lll n^{2/3}$, up to logarithmic factors. However, if $s_0\ggg n^{2/3}$, the unadjusted scheme cannot be efficient in certain directions $a_0$. In the latter regime, it it necessary to modify existing procedures by an adjustment that accounts for the degrees-of-freedom of the Lasso. The proposed degrees-of-freedom adjustment grants asymptotic efficiency for any direction $a_0$. This holds under a Sparse Riecz Condition on the covariance matrix $\Sigma$ and the sample size requirement $s_0/p\to0$ and $s_0\log(p/s_0)/n\to0$. Our analysis also highlights that the degrees-of-freedom adjustment is not necessary when the initial bias of the Lasso in the direction $a_0$ is small, which is granted under more stringent conditions on $\Sigma^{-1}$. This explains why the necessity of degrees-of-freedom adjustment did not appear in some previous studies. The main proof argument involves a Gaussian interpolation path similar to that used to derive Slepian's lemma. It yields a sharp $\ell_\infty$ error bound for the Lasso under Gaussian design which is of independent interest.

Statistically Optimal and Computationally Efficient Low Rank Tensor Completion from Noisy Entries

In this article, we develop methods for estimating a low rank tensor from noisy observations on a subset of its entries to achieve both statistical and computational efficiencies. There have been a lot of recent interests in this problem of noisy tensor completion. Much of the attention has been focused on the fundamental computational challenges often associated with problems involving higher order tensors, yet very little is known about their statistical performance. To fill in this void, in this article, we characterize the fundamental statistical limits of noisy tensor completion by establishing minimax optimal rates of convergence for estimating a $k$th order low rank tensor under the general $\ell_p$ ($1\le p\le 2$) norm which suggest significant room for improvement over the existing approaches. Furthermore, we propose a polynomial-time computable estimating procedure based upon power iteration and a second-order spectral initialization that achieves the optimal rates of convergence. Our method is fairly easy to implement and numerical experiments are presented to further demonstrate the practical merits of our estimator.

Theory of the GMM Kernel

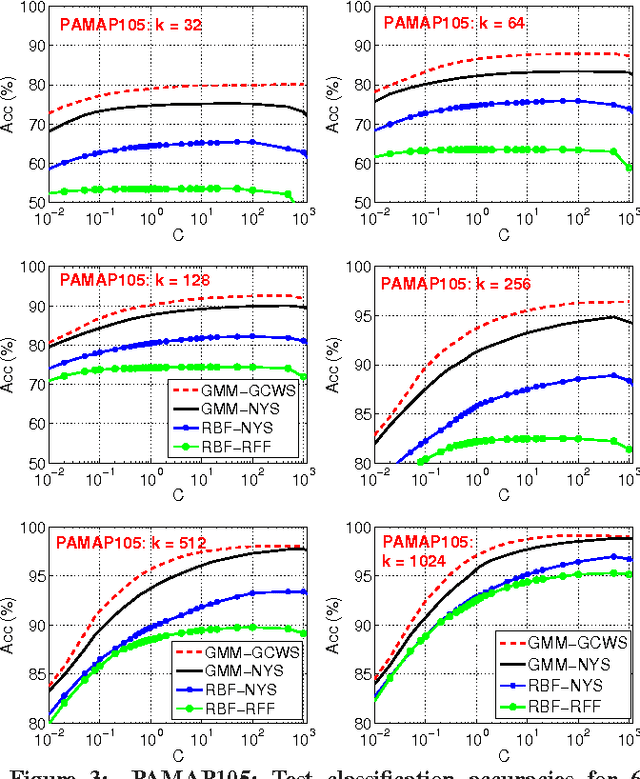
We develop some theoretical results for a robust similarity measure named "generalized min-max" (GMM). This similarity has direct applications in machine learning as a positive definite kernel and can be efficiently computed via probabilistic hashing. Owing to the discrete nature, the hashed values can also be used for efficient near neighbor search. We prove the theoretical limit of GMM and the consistency result, assuming that the data follow an elliptical distribution, which is a very general family of distributions and includes the multivariate $t$-distribution as a special case. The consistency result holds as long as the data have bounded first moment (an assumption which essentially holds for datasets commonly encountered in practice). Furthermore, we establish the asymptotic normality of GMM. Compared to the "cosine" similarity which is routinely adopted in current practice in statistics and machine learning, the consistency of GMM requires much weaker conditions. Interestingly, when the data follow the $t$-distribution with $\nu$ degrees of freedom, GMM typically provides a better measure of similarity than "cosine" roughly when $\nu<8$ (which is already very close to normal). These theoretical results will help explain the recent success of GMM in learning tasks.