TransST: Transfer Learning Embedded Spatial Factor Modeling of Spatial Transcriptomics Data

Background: Spatial transcriptomics have emerged as a powerful tool in biomedical research because of its ability to capture both the spatial contexts and abundance of the complete RNA transcript profile in organs of interest. However, limitations of the technology such as the relatively low resolution and comparatively insufficient sequencing depth make it difficult to reliably extract real biological signals from these data. To alleviate this challenge, we propose a novel transfer learning framework, referred to as TransST, to adaptively leverage the cell-labeled information from external sources in inferring cell-level heterogeneity of a target spatial transcriptomics data. Results: Applications in several real studies as well as a number of simulation settings show that our approach significantly improves existing techniques. For example, in the breast cancer study, TransST successfully identifies five biologically meaningful cell clusters, including the two subgroups of cancer in situ and invasive cancer; in addition, only TransST is able to separate the adipose tissues from the connective issues among all the studied methods. Conclusions: In summary, the proposed method TransST is both effective and robust in identifying cell subclusters and detecting corresponding driving biomarkers in spatial transcriptomics data.

DenseFormer: Learning Dense Depth Map from Sparse Depth and Image via Conditional Diffusion Model

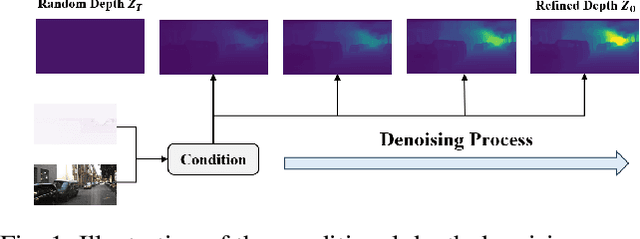
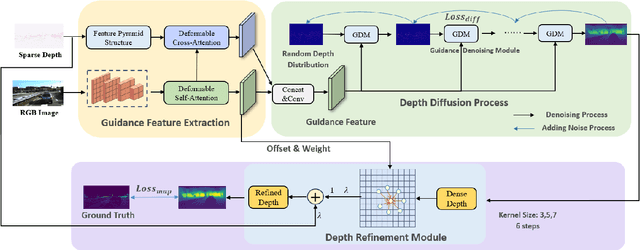
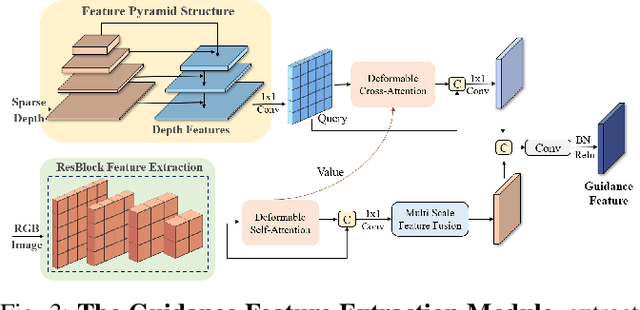
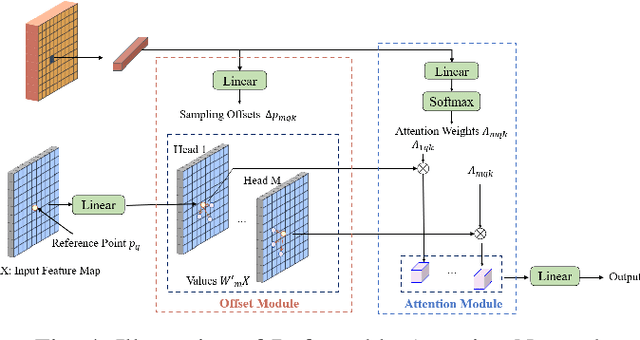
The depth completion task is a critical problem in autonomous driving, involving the generation of dense depth maps from sparse depth maps and RGB images. Most existing methods employ a spatial propagation network to iteratively refine the depth map after obtaining an initial dense depth. In this paper, we propose DenseFormer, a novel method that integrates the diffusion model into the depth completion task. By incorporating the denoising mechanism of the diffusion model, DenseFormer generates the dense depth map by progressively refining an initial random depth distribution through multiple iterations. We propose a feature extraction module that leverages a feature pyramid structure, along with multi-layer deformable attention, to effectively extract and integrate features from sparse depth maps and RGB images, which serve as the guiding condition for the diffusion process. Additionally, this paper presents a depth refinement module that applies multi-step iterative refinement across various ranges to the dense depth results generated by the diffusion process. The module utilizes image features enriched with multi-scale information and sparse depth input to further enhance the accuracy of the predicted depth map. Extensive experiments on the KITTI outdoor scene dataset demonstrate that DenseFormer outperforms classical depth completion methods.

V2X-DGPE: Addressing Domain Gaps and Pose Errors for Robust Collaborative 3D Object Detection

In V2X collaborative perception, the domain gaps between heterogeneous nodes pose a significant challenge for effective information fusion. Pose errors arising from latency and GPS localization noise further exacerbate the issue by leading to feature misalignment. To overcome these challenges, we propose V2X-DGPE, a high-accuracy and robust V2X feature-level collaborative perception framework. V2X-DGPE employs a Knowledge Distillation Framework and a Feature Compensation Module to learn domain-invariant representations from multi-source data, effectively reducing the feature distribution gap between vehicles and roadside infrastructure. Historical information is utilized to provide the model with a more comprehensive understanding of the current scene. Furthermore, a Collaborative Fusion Module leverages a heterogeneous self-attention mechanism to extract and integrate heterogeneous representations from vehicles and infrastructure. To address pose errors, V2X-DGPE introduces a deformable attention mechanism, enabling the model to adaptively focus on critical parts of the input features by dynamically offsetting sampling points. Extensive experiments on the real-world DAIR-V2X dataset demonstrate that the proposed method outperforms existing approaches, achieving state-of-the-art detection performance. The code is available at https://github.com/wangsch10/V2X-DGPE.

XLD: A Cross-Lane Dataset for Benchmarking Novel Driving View Synthesis

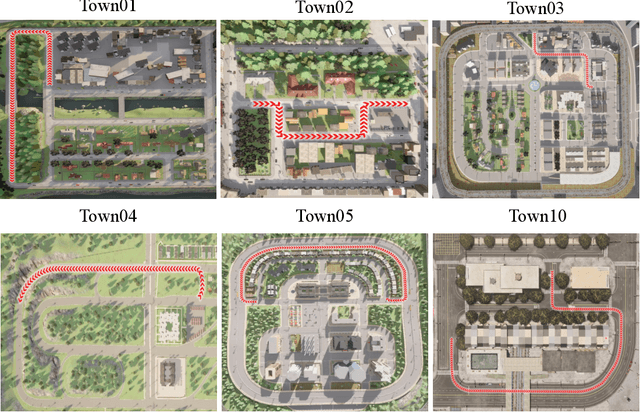
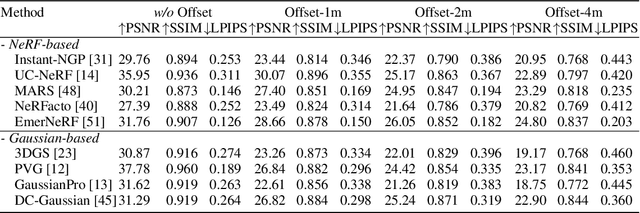
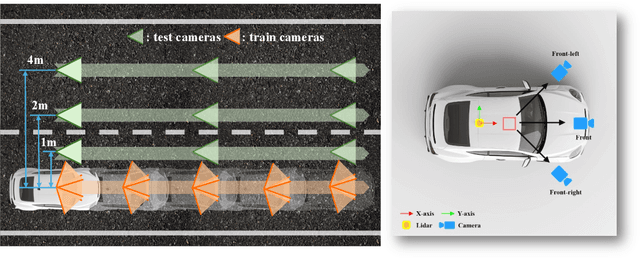
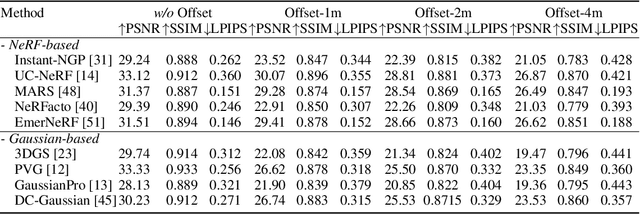
Thoroughly testing autonomy systems is crucial in the pursuit of safe autonomous driving vehicles. It necessitates creating safety-critical scenarios that go beyond what can be safely collected from real-world data, as many of these scenarios occur infrequently on public roads. However, the evaluation of most existing NVS methods relies on sporadic sampling of image frames from the training data, comparing the rendered images with ground truth images using metrics. Unfortunately, this evaluation protocol falls short of meeting the actual requirements in closed-loop simulations. Specifically, the true application demands the capability to render novel views that extend beyond the original trajectory (such as cross-lane views), which are challenging to capture in the real world. To address this, this paper presents a novel driving view synthesis dataset and benchmark specifically designed for autonomous driving simulations. This dataset is unique as it includes testing images captured by deviating from the training trajectory by 1-4 meters. It comprises six sequences encompassing various time and weather conditions. Each sequence contains 450 training images, 150 testing images, and their corresponding camera poses and intrinsic parameters. Leveraging this novel dataset, we establish the first realistic benchmark for evaluating existing NVS approaches under front-only and multi-camera settings. The experimental findings underscore the significant gap that exists in current approaches, revealing their inadequate ability to fulfill the demanding prerequisites of cross-lane or closed-loop simulation. Our dataset is released publicly at the project page: https://3d-aigc.github.io/XLD/.

Tensor Methods in High Dimensional Data Analysis: Opportunities and Challenges

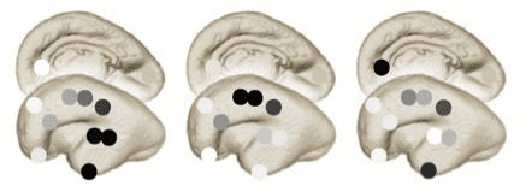
Large amount of multidimensional data represented by multiway arrays or tensors are prevalent in modern applications across various fields such as chemometrics, genomics, physics, psychology, and signal processing. The structural complexity of such data provides vast new opportunities for modeling and analysis, but efficiently extracting information content from them, both statistically and computationally, presents unique and fundamental challenges. Addressing these challenges requires an interdisciplinary approach that brings together tools and insights from statistics, optimization and numerical linear algebra among other fields. Despite these hurdles, significant progress has been made in the last decade. This review seeks to examine some of the key advancements and identify common threads among them, under eight different statistical settings.

Multiple Testing of Linear Forms for Noisy Matrix Completion

Many important tasks of large-scale recommender systems can be naturally cast as testing multiple linear forms for noisy matrix completion. These problems, however, present unique challenges because of the subtle bias-and-variance tradeoff of and an intricate dependence among the estimated entries induced by the low-rank structure. In this paper, we develop a general approach to overcome these difficulties by introducing new statistics for individual tests with sharp asymptotics both marginally and jointly, and utilizing them to control the false discovery rate (FDR) via a data splitting and symmetric aggregation scheme. We show that valid FDR control can be achieved with guaranteed power under nearly optimal sample size requirements using the proposed methodology. Extensive numerical simulations and real data examples are also presented to further illustrate its practical merits.

Mode-wise Principal Subspace Pursuit and Matrix Spiked Covariance Model

This paper introduces a novel framework called Mode-wise Principal Subspace Pursuit (MOP-UP) to extract hidden variations in both the row and column dimensions for matrix data. To enhance the understanding of the framework, we introduce a class of matrix-variate spiked covariance models that serve as inspiration for the development of the MOP-UP algorithm. The MOP-UP algorithm consists of two steps: Average Subspace Capture (ASC) and Alternating Projection (AP). These steps are specifically designed to capture the row-wise and column-wise dimension-reduced subspaces which contain the most informative features of the data. ASC utilizes a novel average projection operator as initialization and achieves exact recovery in the noiseless setting. We analyze the convergence and non-asymptotic error bounds of MOP-UP, introducing a blockwise matrix eigenvalue perturbation bound that proves the desired bound, where classic perturbation bounds fail. The effectiveness and practical merits of the proposed framework are demonstrated through experiments on both simulated and real datasets. Lastly, we discuss generalizations of our approach to higher-order data.

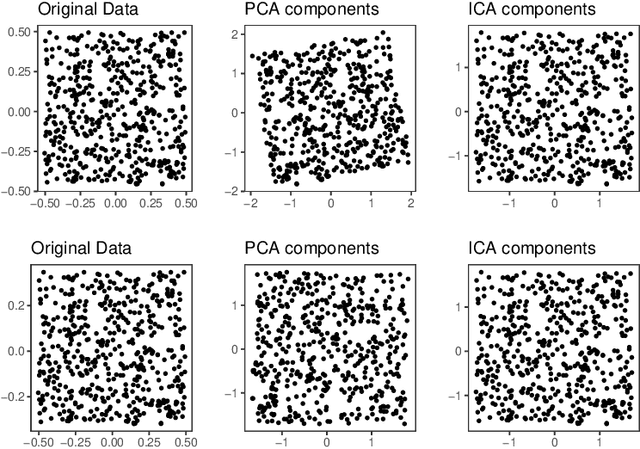
Large Dimensional Independent Component Analysis: Statistical Optimality and Computational Tractability

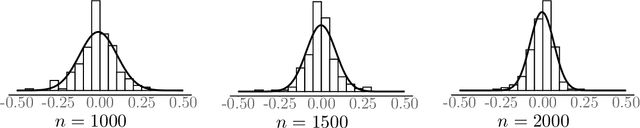
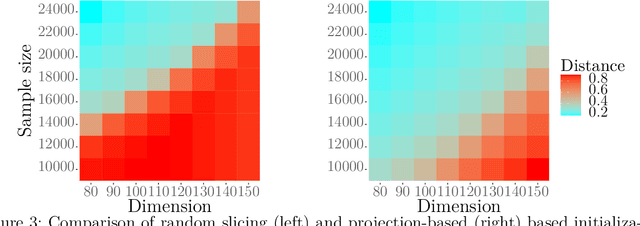
In this paper, we investigate the optimal statistical performance and the impact of computational constraints for independent component analysis (ICA). Our goal is twofold. On the one hand, we characterize the precise role of dimensionality on sample complexity and statistical accuracy, and how computational consideration may affect them. In particular, we show that the optimal sample complexity is linear in dimensionality, and interestingly, the commonly used sample kurtosis-based approaches are necessarily suboptimal. However, the optimal sample complexity becomes quadratic, up to a logarithmic factor, in the dimension if we restrict ourselves to estimates that can be computed with low-degree polynomial algorithms. On the other hand, we develop computationally tractable estimates that attain both the optimal sample complexity and minimax optimal rates of convergence. We study the asymptotic properties of the proposed estimates and establish their asymptotic normality that can be readily used for statistical inferences. Our method is fairly easy to implement and numerical experiments are presented to further demonstrate its practical merits.

On Recovering the Best Rank-r Approximation from Few Entries

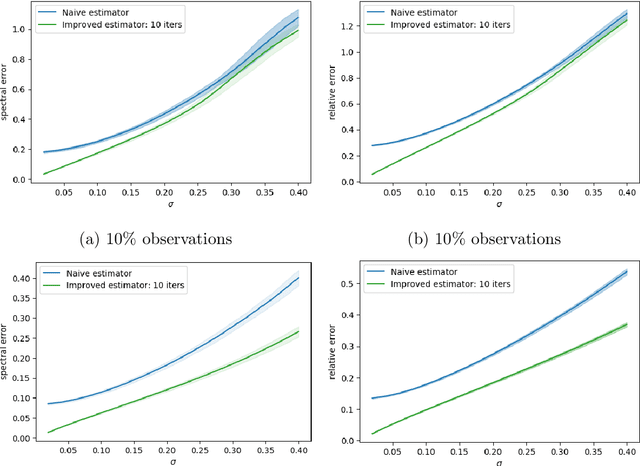
In this note, we investigate how well we can reconstruct the best rank-$r$ approximation of a large matrix from a small number of its entries. We show that even if a data matrix is of full rank and cannot be approximated well by a low-rank matrix, its best low-rank approximations may still be reliably computed or estimated from a small number of its entries. This is especially relevant from a statistical viewpoint: the best low-rank approximations to a data matrix are often of more interest than itself because they capture the more stable and oftentimes more reproducible properties of an otherwise complicated data-generating model. In particular, we investigate two agnostic approaches: the first is based on spectral truncation; and the second is a projected gradient descent based optimization procedure. We argue that, while the first approach is intuitive and reasonably effective, the latter has far superior performance in general. We show that the error depends on how close the matrix is to being of low rank. Both theoretical and numerical evidence is presented to demonstrate the effectiveness of the proposed approaches.

On Estimating Rank-One Spiked Tensors in the Presence of Heavy Tailed Errors

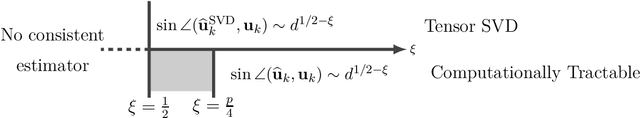
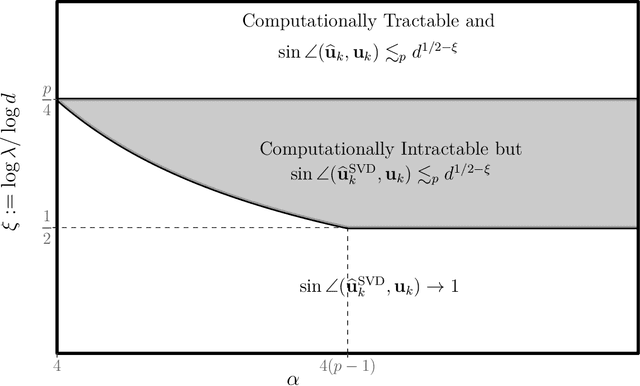
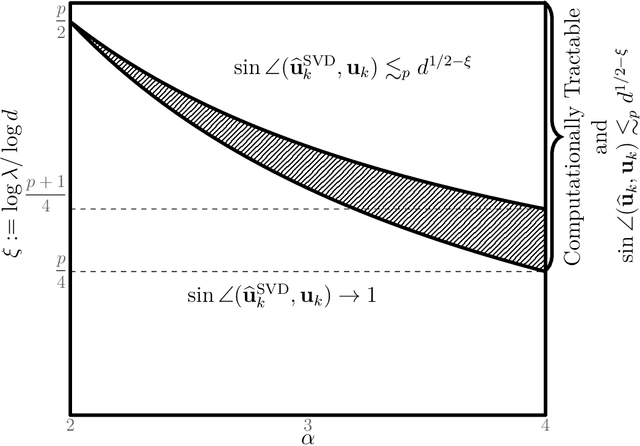
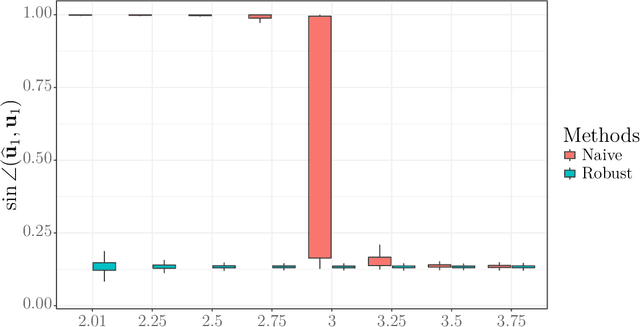
In this paper, we study the estimation of a rank-one spiked tensor in the presence of heavy tailed noise. Our results highlight some of the fundamental similarities and differences in the tradeoff between statistical and computational efficiencies under heavy tailed and Gaussian noise. In particular, we show that, for $p$ th order tensors, the tradeoff manifests in an identical fashion as the Gaussian case when the noise has finite $4(p-1)$ th moment. The difference in signal strength requirements, with or without computational constraints, for us to estimate the singular vectors at the optimal rate, interestingly, narrows for noise with heavier tails and vanishes when the noise only has finite fourth moment. Moreover, if the noise has less than fourth moment, tensor SVD, perhaps the most natural approach, is suboptimal even though it is computationally intractable. Our analysis exploits a close connection between estimating the rank-one spikes and the spectral norm of a random tensor with iid entries. In particular, we show that the order of the spectral norm of a random tensor can be precisely characterized by the moment of its entries, generalizing classical results for random matrices. In addition to the theoretical guarantees, we propose estimation procedures for the heavy tailed regime, which are easy to implement and efficient to run. Numerical experiments are presented to demonstrate their practical merits.