TEAFormers: TEnsor-Augmented Transformers for Multi-Dimensional Time Series Forecasting

Multi-dimensional time series data, such as matrix and tensor-variate time series, are increasingly prevalent in fields such as economics, finance, and climate science. Traditional Transformer models, though adept with sequential data, do not effectively preserve these multi-dimensional structures, as their internal operations in effect flatten multi-dimensional observations into vectors, thereby losing critical multi-dimensional relationships and patterns. To address this, we introduce the Tensor-Augmented Transformer (TEAFormer), a novel method that incorporates tensor expansion and compression within the Transformer framework to maintain and leverage the inherent multi-dimensional structures, thus reducing computational costs and improving prediction accuracy. The core feature of the TEAFormer, the Tensor-Augmentation (TEA) module, utilizes tensor expansion to enhance multi-view feature learning and tensor compression for efficient information aggregation and reduced computational load. The TEA module is not just a specific model architecture but a versatile component that is highly compatible with the attention mechanism and the encoder-decoder structure of Transformers, making it adaptable to existing Transformer architectures. Our comprehensive experiments, which integrate the TEA module into three popular time series Transformer models across three real-world benchmarks, show significant performance enhancements, highlighting the potential of TEAFormers for cutting-edge time series forecasting.

High-Dimensional Tensor Discriminant Analysis with Incomplete Tensors

Tensor classification has gained prominence across various fields, yet the challenge of handling partially observed tensor data in real-world applications remains largely unaddressed. This paper introduces a novel approach to tensor classification with incomplete data, framed within the tensor high-dimensional linear discriminant analysis. Specifically, we consider a high-dimensional tensor predictor with missing observations under the Missing Completely at Random (MCR) assumption and employ the Tensor Gaussian Mixture Model to capture the relationship between the tensor predictor and class label. We propose the Tensor LDA-MD algorithm, which manages high-dimensional tensor predictors with missing entries by leveraging the low-rank structure of the discriminant tensor. A key feature of our approach is a novel covariance estimation method under the tensor-based MCR model, supported by theoretical results that allow for correlated entries under mild conditions. Our work establishes the convergence rate of the estimation error of the discriminant tensor with incomplete data and minimax optimal bounds for the misclassification rate, addressing key gaps in the literature. Additionally, we derive large deviation results for the generalized mode-wise (separable) sample covariance matrix and its inverse, which are crucial tools in our analysis and hold independent interest. Our method demonstrates excellent performance in simulations and real data analysis, even with significant proportions of missing data. This research advances high-dimensional LDA and tensor learning, providing practical tools for applications with incomplete data and a solid theoretical foundation for classification accuracy in complex settings.

Factor Augmented Tensor-on-Tensor Neural Networks

This paper studies the prediction task of tensor-on-tensor regression in which both covariates and responses are multi-dimensional arrays (a.k.a., tensors) across time with arbitrary tensor order and data dimension. Existing methods either focused on linear models without accounting for possibly nonlinear relationships between covariates and responses, or directly employed black-box deep learning algorithms that failed to utilize the inherent tensor structure. In this work, we propose a Factor Augmented Tensor-on-Tensor Neural Network (FATTNN) that integrates tensor factor models into deep neural networks. We begin with summarizing and extracting useful predictive information (represented by the ``factor tensor'') from the complex structured tensor covariates, and then proceed with the prediction task using the estimated factor tensor as input of a temporal convolutional neural network. The proposed methods effectively handle nonlinearity between complex data structures, and improve over traditional statistical models and conventional deep learning approaches in both prediction accuracy and computational cost. By leveraging tensor factor models, our proposed methods exploit the underlying latent factor structure to enhance the prediction, and in the meantime, drastically reduce the data dimensionality that speeds up the computation. The empirical performances of our proposed methods are demonstrated via simulation studies and real-world applications to three public datasets. Numerical results show that our proposed algorithms achieve substantial increases in prediction accuracy and significant reductions in computational time compared to benchmark methods.

Tensor Principal Component Analysis in High Dimensional CP Models

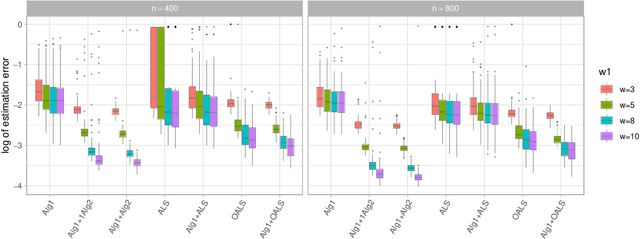
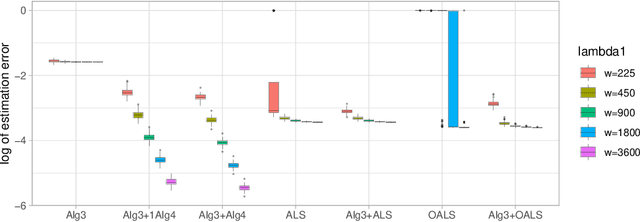
The CP decomposition for high dimensional non-orthogonal spike tensors is an important problem with broad applications across many disciplines. However, previous works with theoretical guarantee typically assume restrictive incoherence conditions on the basis vectors for the CP components. In this paper, we propose new computationally efficient composite PCA and concurrent orthogonalization algorithms for tensor CP decomposition with theoretical guarantees under mild incoherence conditions. The composite PCA applies the principal component or singular value decompositions twice, first to a matrix unfolding of the tensor data to obtain singular vectors and then to the matrix folding of the singular vectors obtained in the first step. It can be used as an initialization for any iterative optimization schemes for the tensor CP decomposition. The concurrent orthogonalization algorithm iteratively estimates the basis vector in each mode of the tensor by simultaneously applying projections to the orthogonal complements of the spaces generated by others CP components in other modes. It is designed to improve the alternating least squares estimator and other forms of the high order orthogonal iteration for tensors with low or moderately high CP ranks. Our theoretical investigation provides estimation accuracy and statistical convergence rates for the two proposed algorithms. Our implementations on synthetic data demonstrate significant practical superiority of our approach over existing methods.