Factor Augmented Tensor-on-Tensor Neural Networks

This paper studies the prediction task of tensor-on-tensor regression in which both covariates and responses are multi-dimensional arrays (a.k.a., tensors) across time with arbitrary tensor order and data dimension. Existing methods either focused on linear models without accounting for possibly nonlinear relationships between covariates and responses, or directly employed black-box deep learning algorithms that failed to utilize the inherent tensor structure. In this work, we propose a Factor Augmented Tensor-on-Tensor Neural Network (FATTNN) that integrates tensor factor models into deep neural networks. We begin with summarizing and extracting useful predictive information (represented by the ``factor tensor'') from the complex structured tensor covariates, and then proceed with the prediction task using the estimated factor tensor as input of a temporal convolutional neural network. The proposed methods effectively handle nonlinearity between complex data structures, and improve over traditional statistical models and conventional deep learning approaches in both prediction accuracy and computational cost. By leveraging tensor factor models, our proposed methods exploit the underlying latent factor structure to enhance the prediction, and in the meantime, drastically reduce the data dimensionality that speeds up the computation. The empirical performances of our proposed methods are demonstrated via simulation studies and real-world applications to three public datasets. Numerical results show that our proposed algorithms achieve substantial increases in prediction accuracy and significant reductions in computational time compared to benchmark methods.

A Unified Combination Framework for Dependent Tests with Applications to Microbiome Association Studies

We introduce a novel meta-analysis framework to combine dependent tests under a general setting, and utilize it to synthesize various microbiome association tests that are calculated from the same dataset. Our development builds upon the classical meta-analysis methods of aggregating $p$-values and also a more recent general method of combining confidence distributions, but makes generalizations to handle dependent tests. The proposed framework ensures rigorous statistical guarantees, and we provide a comprehensive study and compare it with various existing dependent combination methods. Notably, we demonstrate that the widely used Cauchy combination method for dependent tests, referred to as the vanilla Cauchy combination in this article, can be viewed as a special case within our framework. Moreover, the proposed framework provides a way to address the problem when the distributional assumptions underlying the vanilla Cauchy combination are violated. Our numerical results demonstrate that ignoring the dependence among the to-be-combined components may lead to a severe size distortion phenomenon. Compared to the existing $p$-value combination methods, including the vanilla Cauchy combination method, the proposed combination framework can handle the dependence accurately and utilizes the information efficiently to construct tests with accurate size and enhanced power. The development is applied to Microbiome Association Studies, where we aggregate information from multiple existing tests using the same dataset. The combined tests harness the strengths of each individual test across a wide range of alternative spaces, %resulting in a significant enhancement of testing power across a wide range of alternative spaces, enabling more efficient and meaningful discoveries of vital microbiome associations.

Generalized Causal Tree for Uplift Modeling

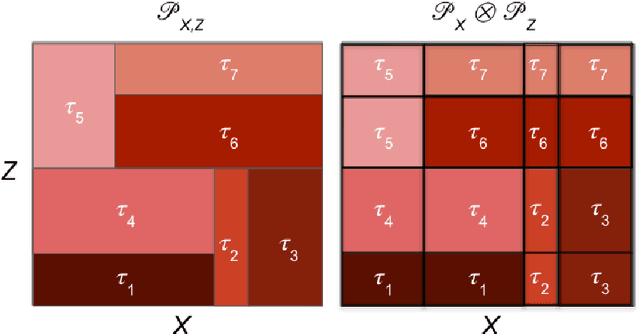
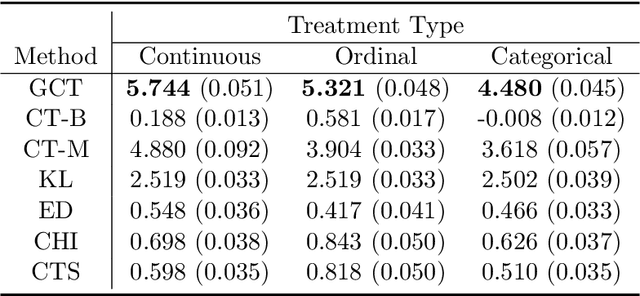
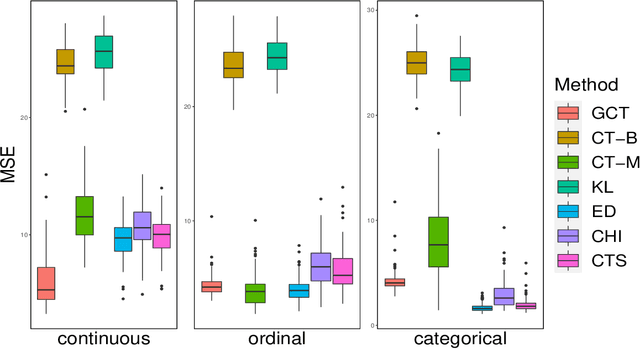
Uplift modeling is crucial in various applications ranging from marketing and policy-making to personalized recommendations. The main objective is to learn optimal treatment allocations for a heterogeneous population. A primary line of existing work modifies the loss function of the decision tree algorithm to identify cohorts with heterogeneous treatment effects. Another line of work estimates the individual treatment effects separately for the treatment group and the control group using off-the-shelf supervised learning algorithms. The former approach that directly models the heterogeneous treatment effect is known to outperform the latter in practice. However, the existing tree-based methods are mostly limited to a single treatment and a single control use case, except for a handful of extensions to multiple discrete treatments. In this paper, we fill this gap in the literature by proposing a generalization to the tree-based approaches to tackle multiple discrete and continuous-valued treatments. We focus on a generalization of the well-known causal tree algorithm due to its desirable statistical properties, but our generalization technique can be applied to other tree-based approaches as well. We perform extensive experiments to showcase the efficacy of our method when compared to other methods.

Fisher's combined probability test for high-dimensional covariance matrices

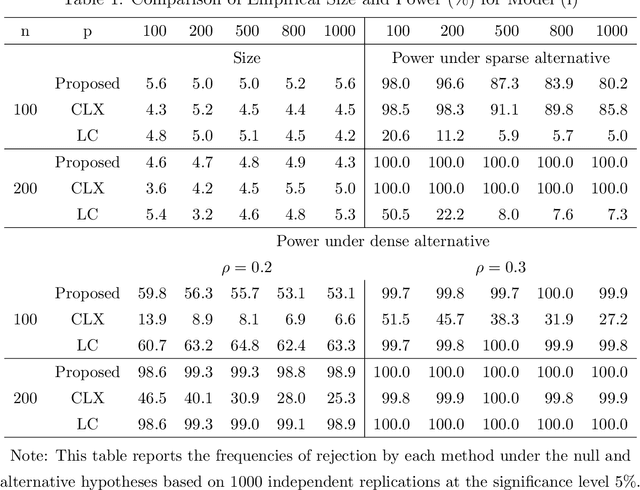
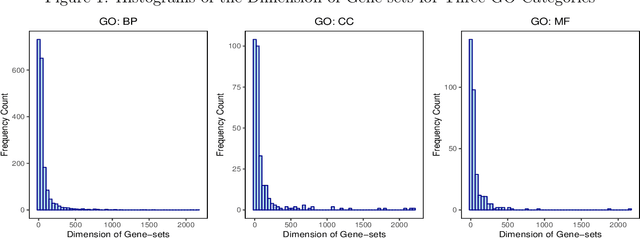
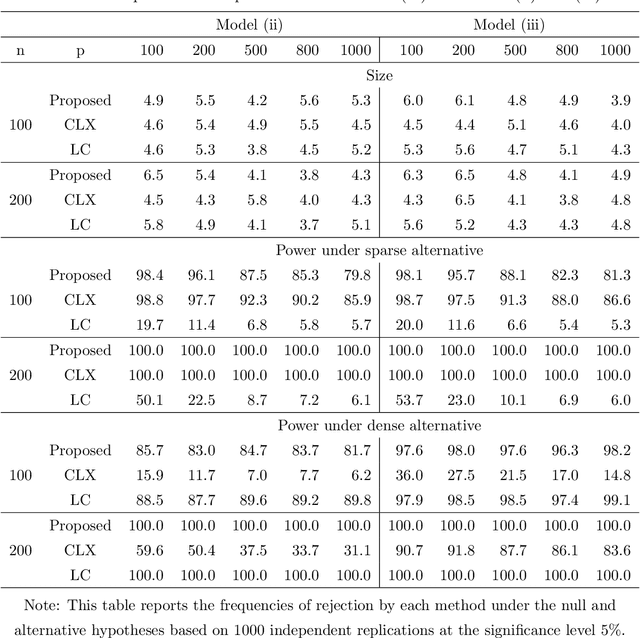
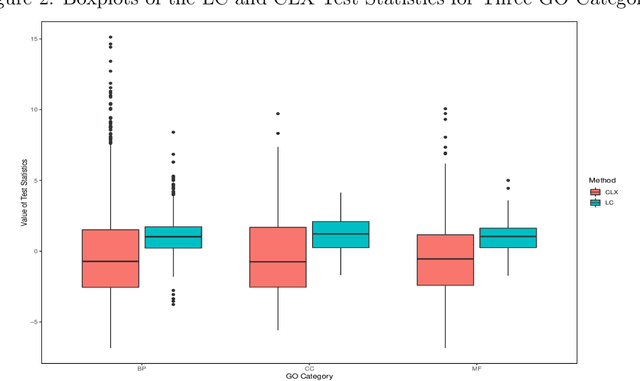
Testing large covariance matrices is of fundamental importance in statistical analysis with high-dimensional data. In the past decade, three types of test statistics have been studied in the literature: quadratic form statistics, maximum form statistics, and their weighted combination. It is known that quadratic form statistics would suffer from low power against sparse alternatives and maximum form statistics would suffer from low power against dense alternatives. The weighted combination methods were introduced to enhance the power of quadratic form statistics or maximum form statistics when the weights are appropriately chosen. In this paper, we provide a new perspective to exploit the full potential of quadratic form statistics and maximum form statistics for testing high-dimensional covariance matrices. We propose a scale-invariant power enhancement test based on Fisher's method to combine the p-values of quadratic form statistics and maximum form statistics. After carefully studying the asymptotic joint distribution of quadratic form statistics and maximum form statistics, we prove that the proposed combination method retains the correct asymptotic size and boosts the power against more general alternatives. Moreover, we demonstrate the finite-sample performance in simulation studies and a real application.