Pushing the limits of fairness impossibility: Who's the fairest of them all?

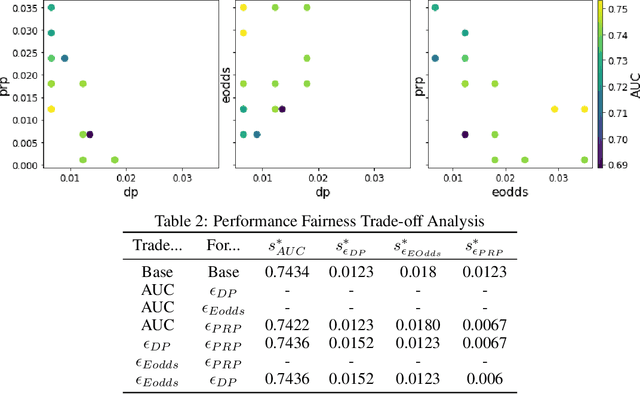
The impossibility theorem of fairness is a foundational result in the algorithmic fairness literature. It states that outside of special cases, one cannot exactly and simultaneously satisfy all three common and intuitive definitions of fairness - demographic parity, equalized odds, and predictive rate parity. This result has driven most works to focus on solutions for one or two of the metrics. Rather than follow suit, in this paper we present a framework that pushes the limits of the impossibility theorem in order to satisfy all three metrics to the best extent possible. We develop an integer-programming based approach that can yield a certifiably optimal post-processing method for simultaneously satisfying multiple fairness criteria under small violations. We show experiments demonstrating that our post-processor can improve fairness across the different definitions simultaneously with minimal model performance reduction. We also discuss applications of our framework for model selection and fairness explainability, thereby attempting to answer the question: who's the fairest of them all?

Generalized Causal Tree for Uplift Modeling

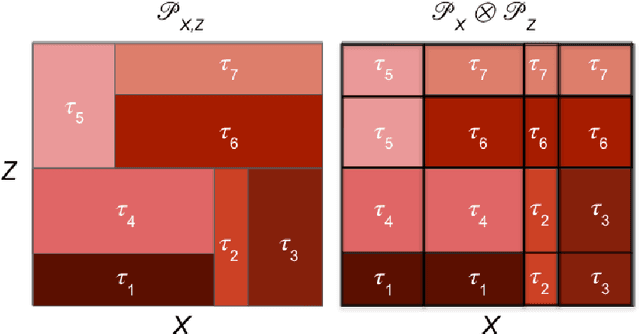
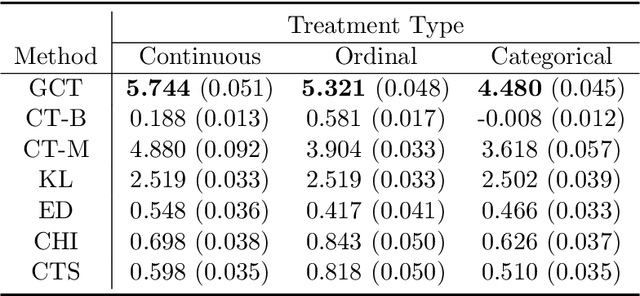
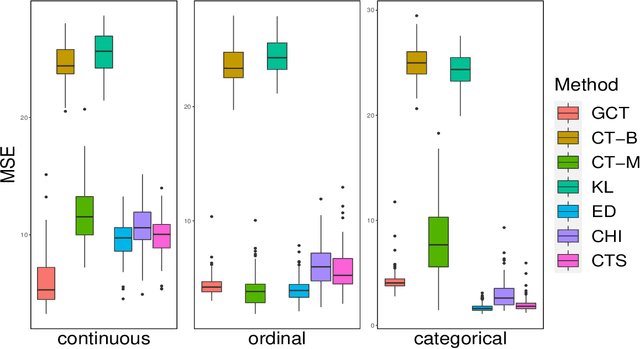
Uplift modeling is crucial in various applications ranging from marketing and policy-making to personalized recommendations. The main objective is to learn optimal treatment allocations for a heterogeneous population. A primary line of existing work modifies the loss function of the decision tree algorithm to identify cohorts with heterogeneous treatment effects. Another line of work estimates the individual treatment effects separately for the treatment group and the control group using off-the-shelf supervised learning algorithms. The former approach that directly models the heterogeneous treatment effect is known to outperform the latter in practice. However, the existing tree-based methods are mostly limited to a single treatment and a single control use case, except for a handful of extensions to multiple discrete treatments. In this paper, we fill this gap in the literature by proposing a generalization to the tree-based approaches to tackle multiple discrete and continuous-valued treatments. We focus on a generalization of the well-known causal tree algorithm due to its desirable statistical properties, but our generalization technique can be applied to other tree-based approaches as well. We perform extensive experiments to showcase the efficacy of our method when compared to other methods.

Offline Reinforcement Learning for Mobile Notifications

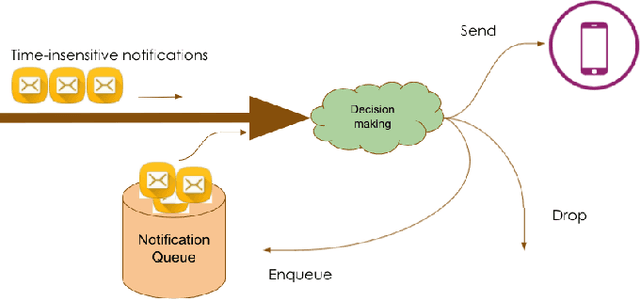
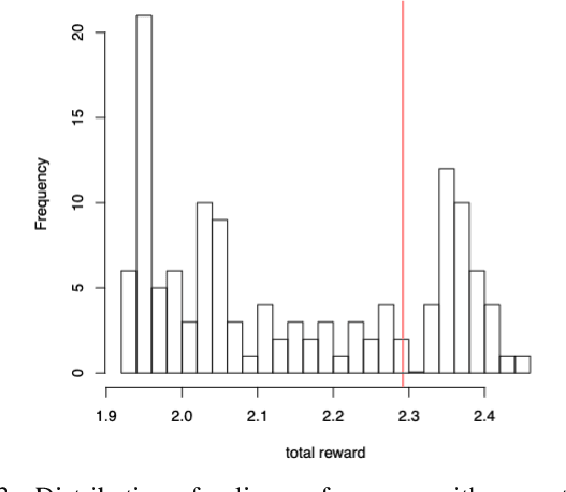
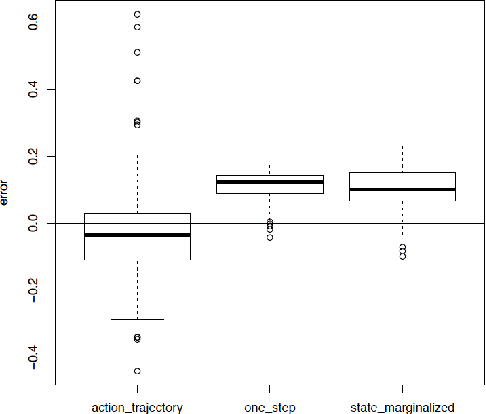
Mobile notification systems have taken a major role in driving and maintaining user engagement for online platforms. They are interesting recommender systems to machine learning practitioners with more sequential and long-term feedback considerations. Most machine learning applications in notification systems are built around response-prediction models, trying to attribute both short-term impact and long-term impact to a notification decision. However, a user's experience depends on a sequence of notifications and attributing impact to a single notification is not always accurate, if not impossible. In this paper, we argue that reinforcement learning is a better framework for notification systems in terms of performance and iteration speed. We propose an offline reinforcement learning framework to optimize sequential notification decisions for driving user engagement. We describe a state-marginalized importance sampling policy evaluation approach, which can be used to evaluate the policy offline and tune learning hyperparameters. Through simulations that approximate the notifications ecosystem, we demonstrate the performance and benefits of the offline evaluation approach as a part of the reinforcement learning modeling approach. Finally, we collect data through online exploration in the production system, train an offline Double Deep Q-Network and launch a successful policy online. We also discuss the practical considerations and results obtained by deploying these policies for a large-scale recommendation system use-case.

Scalable Assessment and Mitigation Strategies for Fairness in Rankings

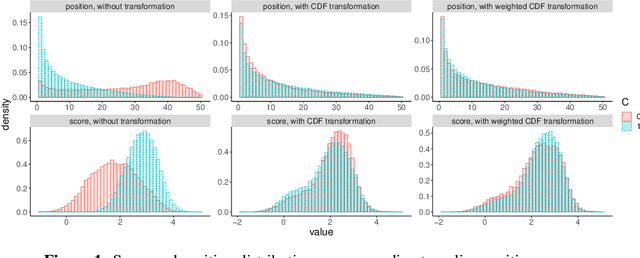
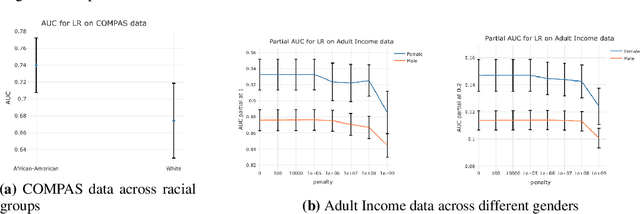
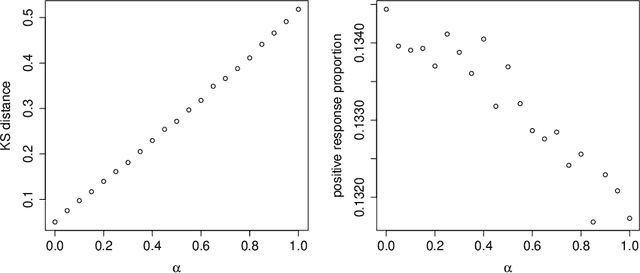
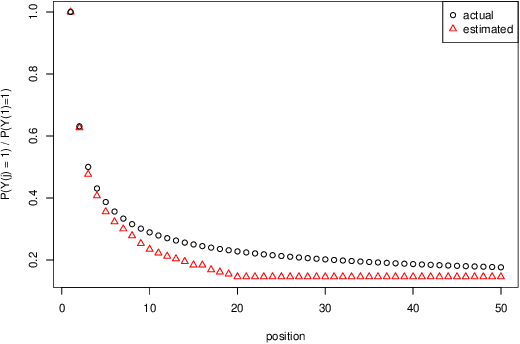
Motivated by industrial-scale applications, we consider two specific areas of fairness, one connected to the notion of equality of opportunity, and the other one generally tied to fair model performance. Throughout the paper, we consider only methods that can be scaled to Internet-industry size datasets. With this in mind, we propose a simple post-processing method to achieve equality of opportunity and discuss challenges and some solutions in the specific cases of recommendation systems and rankings. We then discuss a class of model performance fairness measures based on conditional ROC curves. We propose both scalable uncertainty assessment tools (that improve upon recent research) as well as scalable penalized methods to improve fairness with respect to these metrics. We provide fast algorithms with an emphasis on making few passes over the data when possible.

Optimal Convergence for Stochastic Optimization with Multiple Expectation Constraints

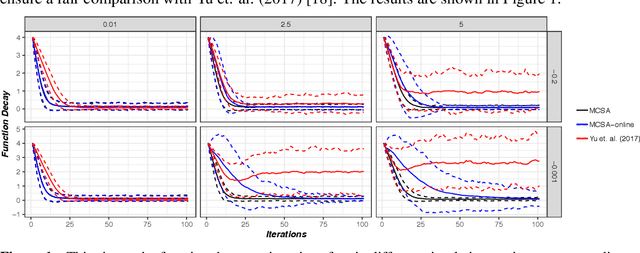
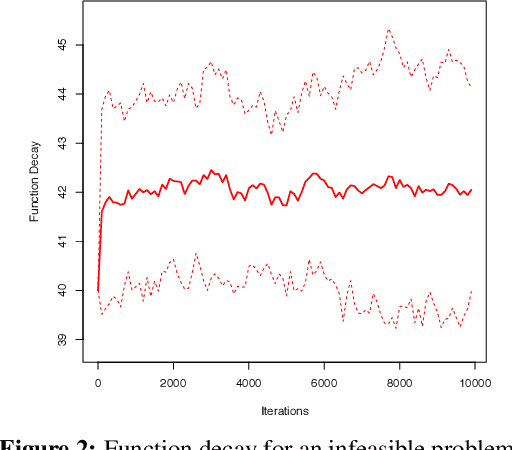
In this paper, we focus on the problem of stochastic optimization where the objective function can be written as an expectation function over a closed convex set. We also consider multiple expectation constraints which restrict the domain of the problem. We extend the cooperative stochastic approximation algorithm from Lan and Zhou [2016] to solve the particular problem. We close the gaps in the previous analysis and provide a novel proof technique to show that our algorithm attains the optimal rate of convergence for both optimality gap and constraint violation when the functions are generally convex. We also compare our algorithm empirically to the state-of-the-art and show improved convergence in many situations.

Inference for Individual Mediation Effects and Interventional Effects in Sparse High-Dimensional Causal Graphical Models

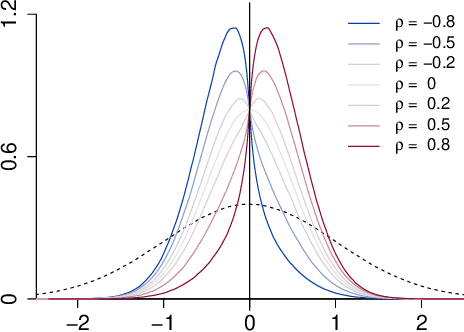
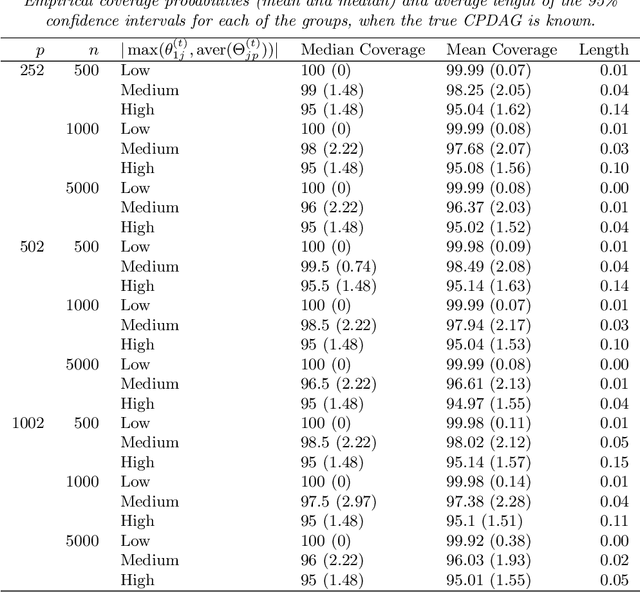
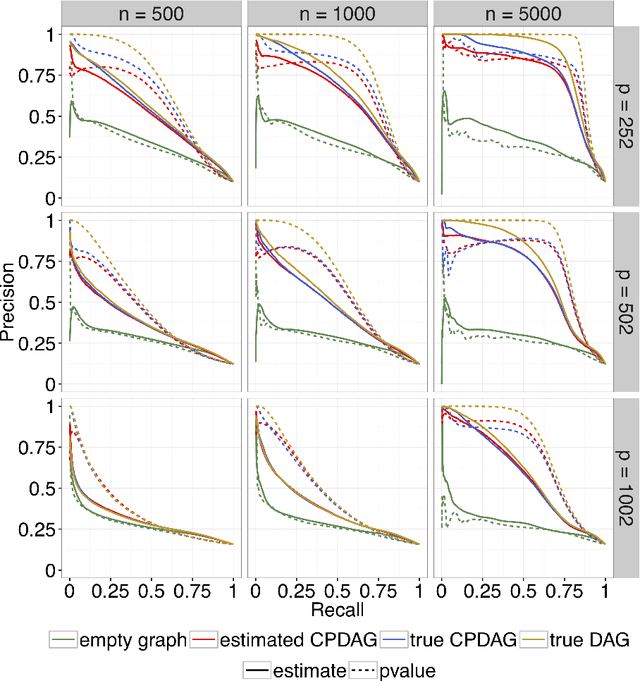
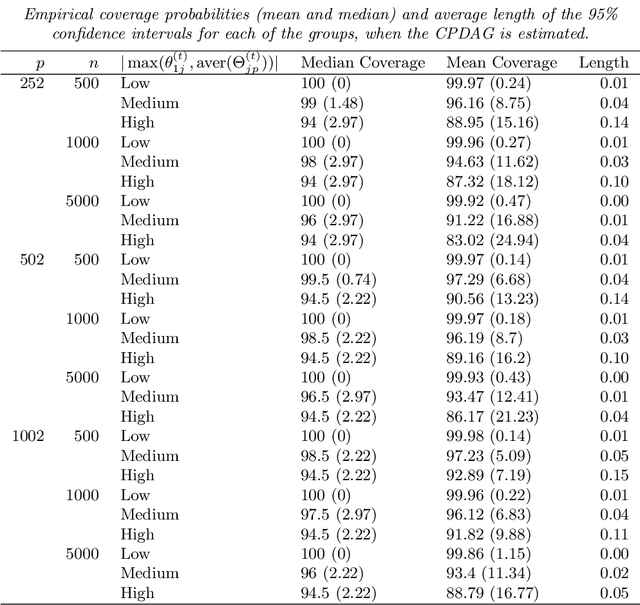
We consider the problem of identifying intermediate variables (or mediators) that regulate the effect of a treatment on a response variable. While there has been significant research on this topic, little work has been done when the set of potential mediators is high-dimensional and when they are interrelated. In particular, we assume that the causal structure of the treatment, the potential mediators and the response is a directed acyclic graph (DAG). High-dimensional DAG models have previously been used for the estimation of causal effects from observational data and methods called IDA and joint-IDA have been developed for estimating the effects of single interventions and multiple simultaneous interventions respectively. In this paper, we propose an IDA-type method called MIDA for estimating mediation effects from high-dimensional observational data. Although IDA and joint-IDA estimators have been shown to be consistent in certain sparse high-dimensional settings, their asymptotic properties such as convergence in distribution and inferential tools in such settings remained unknown. We prove high-dimensional consistency of MIDA for linear structural equation models with sub-Gaussian errors. More importantly, we derive distributional convergence results for MIDA in similar high-dimensional settings, which are applicable to IDA and joint-IDA estimators as well. To the best of our knowledge, these are the first distributional convergence results facilitating inference for IDA-type estimators. These results have been built on our novel theoretical results regarding uniform bounds for linear regression estimators over varying subsets of high-dimensional covariates, which may be of independent interest. Finally, we empirically validate our asymptotic theory and demonstrate the usefulness of MIDA in identifying large mediation effects via simulations and application to real data in genomics.