Bidding Agent Design in the LinkedIn Ad Marketplace

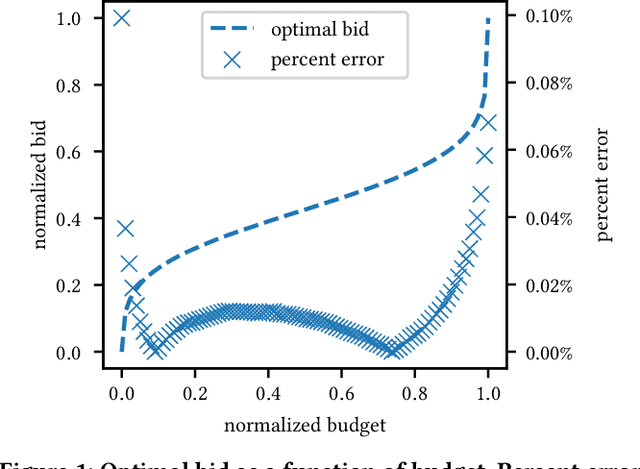
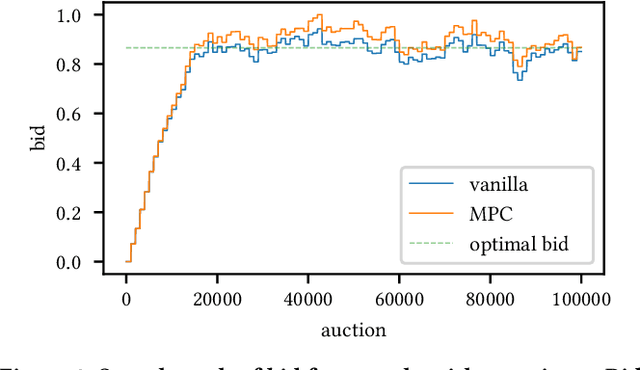
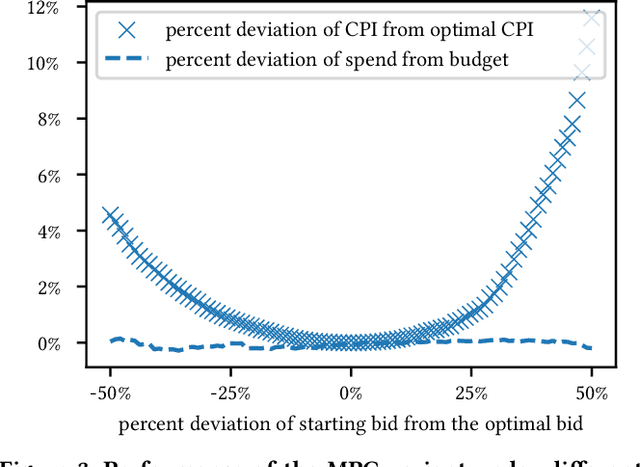
We establish a general optimization framework for the design of automated bidding agent in dynamic online marketplaces. It optimizes solely for the buyer's interest and is agnostic to the auction mechanism imposed by the seller. As a result, the framework allows, for instance, the joint optimization of a group of ads across multiple platforms each running its own auction format. Bidding strategy derived from this framework automatically guarantees the optimality of budget allocation across ad units and platforms. Common constraints such as budget delivery schedule, return on investments and guaranteed results, directly translates to additional parameters in the bidding formula. We share practical learnings of the deployed bidding system in the LinkedIn ad marketplace based on this framework.

A Framework for Fairness in Two-Sided Marketplaces

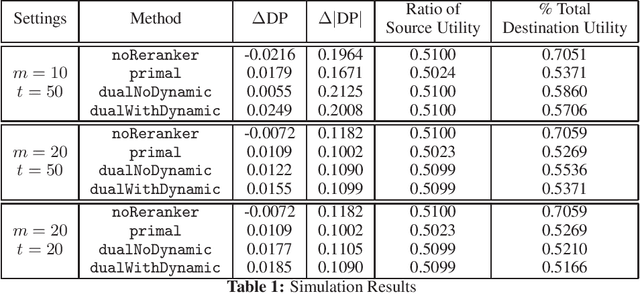
Many interesting problems in the Internet industry can be framed as a two-sided marketplace problem. Examples include search applications and recommender systems showing people, jobs, movies, products, restaurants, etc. Incorporating fairness while building such systems is crucial and can have a deep social and economic impact (applications include job recommendations, recruiters searching for candidates, etc.). In this paper, we propose a definition and develop an end-to-end framework for achieving fairness while building such machine learning systems at scale. We extend prior work to develop an optimization framework that can tackle fairness constraints from both the source and destination sides of the marketplace, as well as dynamic aspects of the problem. The framework is flexible enough to adapt to different definitions of fairness and can be implemented in very large-scale settings. We perform simulations to show the efficacy of our approach.

Scalable Assessment and Mitigation Strategies for Fairness in Rankings

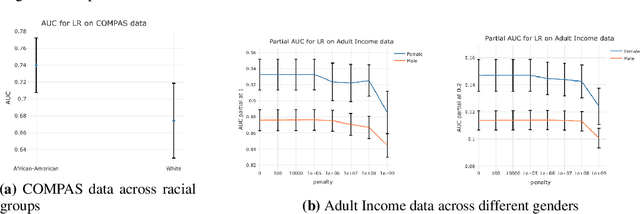
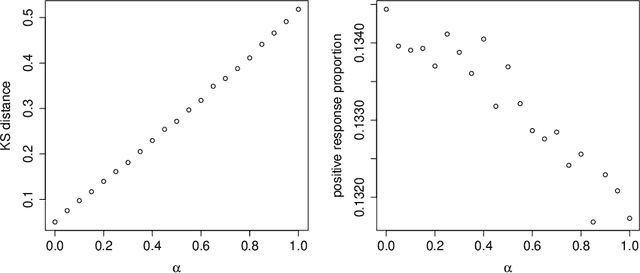
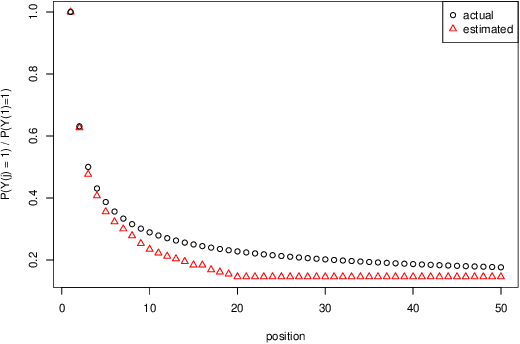
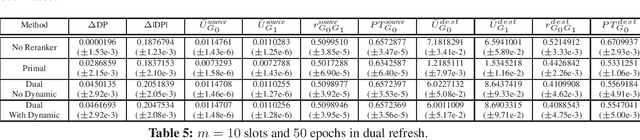
Motivated by industrial-scale applications, we consider two specific areas of fairness, one connected to the notion of equality of opportunity, and the other one generally tied to fair model performance. Throughout the paper, we consider only methods that can be scaled to Internet-industry size datasets. With this in mind, we propose a simple post-processing method to achieve equality of opportunity and discuss challenges and some solutions in the specific cases of recommendation systems and rankings. We then discuss a class of model performance fairness measures based on conditional ROC curves. We propose both scalable uncertainty assessment tools (that improve upon recent research) as well as scalable penalized methods to improve fairness with respect to these metrics. We provide fast algorithms with an emphasis on making few passes over the data when possible.

Can we trust the bootstrap in high-dimension?

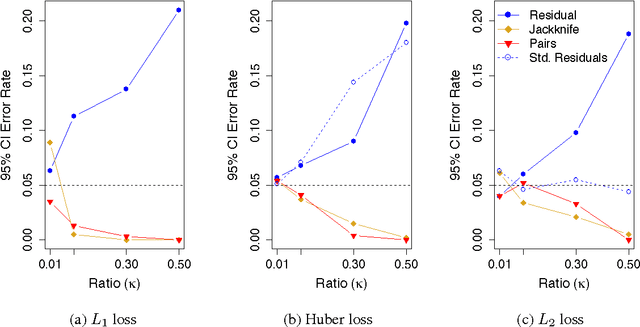
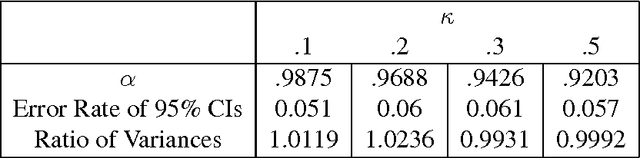
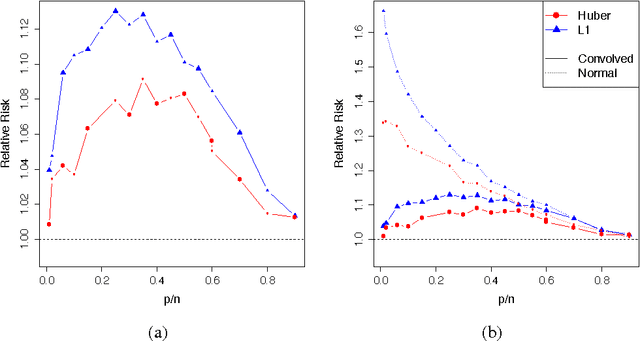
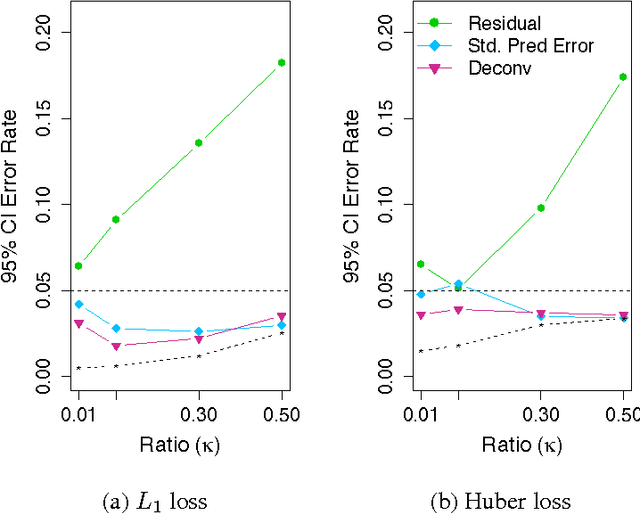
We consider the performance of the bootstrap in high-dimensions for the setting of linear regression, where $p<n$ but $p/n$ is not close to zero. We consider ordinary least-squares as well as robust regression methods and adopt a minimalist performance requirement: can the bootstrap give us good confidence intervals for a single coordinate of $\beta$? (where $\beta$ is the true regression vector). We show through a mix of numerical and theoretical work that the bootstrap is fraught with problems. Both of the most commonly used methods of bootstrapping for regression -- residual bootstrap and pairs bootstrap -- give very poor inference on $\beta$ as the ratio $p/n$ grows. We find that the residuals bootstrap tend to give anti-conservative estimates (inflated Type I error), while the pairs bootstrap gives very conservative estimates (severe loss of power) as the ratio $p/n$ grows. We also show that the jackknife resampling technique for estimating the variance of $\hat{\beta}$ severely overestimates the variance in high dimensions. We contribute alternative bootstrap procedures based on our theoretical results that mitigate these problems. However, the corrections depend on assumptions regarding the underlying data-generation model, suggesting that in high-dimensions it may be difficult to have universal, robust bootstrapping techniques.

Graph connection Laplacian and random matrices with random blocks

Graph connection Laplacian (GCL) is a modern data analysis technique that is starting to be applied for the analysis of high dimensional and massive datasets. Motivated by this technique, we study matrices that are akin to the ones appearing in the null case of GCL, i.e the case where there is no structure in the dataset under investigation. Developing this understanding is important in making sense of the output of the algorithms based on GCL. We hence develop a theory explaining the behavior of the spectral distribution of a large class of random matrices, in particular random matrices with random block entries of fixed size. Part of the theory covers the case where there is significant dependence between the blocks. Numerical work shows that the agreement between our theoretical predictions and numerical simulations is generally very good.

Connection graph Laplacian methods can be made robust to noise

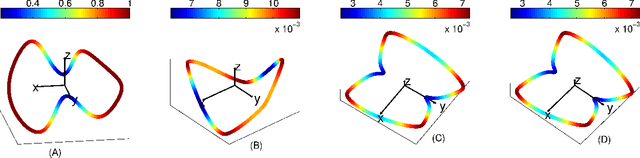
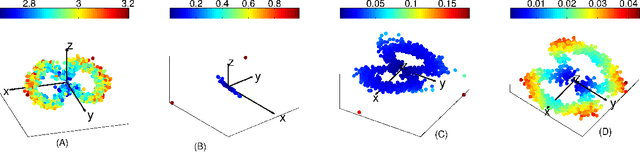
Recently, several data analytic techniques based on connection graph laplacian (CGL) ideas have appeared in the literature. At this point, the properties of these methods are starting to be understood in the setting where the data is observed without noise. We study the impact of additive noise on these methods, and show that they are remarkably robust. As a by-product of our analysis, we propose modifications of the standard algorithms that increase their robustness to noise. We illustrate our results in numerical simulations.