Can we trust the bootstrap in high-dimension?
Paper and Code
Aug 02, 2016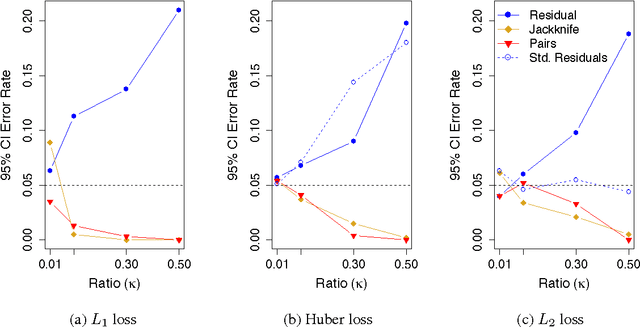
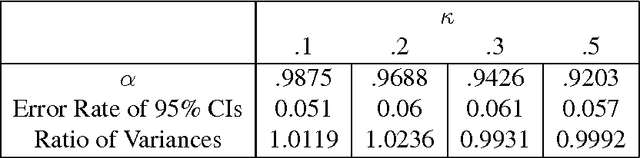
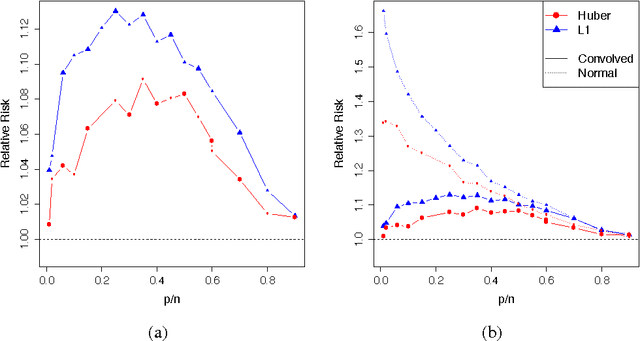
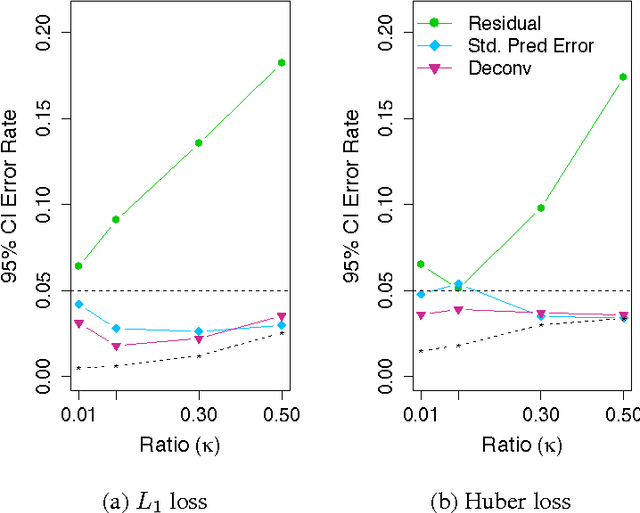
We consider the performance of the bootstrap in high-dimensions for the setting of linear regression, where $p<n$ but $p/n$ is not close to zero. We consider ordinary least-squares as well as robust regression methods and adopt a minimalist performance requirement: can the bootstrap give us good confidence intervals for a single coordinate of $\beta$? (where $\beta$ is the true regression vector). We show through a mix of numerical and theoretical work that the bootstrap is fraught with problems. Both of the most commonly used methods of bootstrapping for regression -- residual bootstrap and pairs bootstrap -- give very poor inference on $\beta$ as the ratio $p/n$ grows. We find that the residuals bootstrap tend to give anti-conservative estimates (inflated Type I error), while the pairs bootstrap gives very conservative estimates (severe loss of power) as the ratio $p/n$ grows. We also show that the jackknife resampling technique for estimating the variance of $\hat{\beta}$ severely overestimates the variance in high dimensions. We contribute alternative bootstrap procedures based on our theoretical results that mitigate these problems. However, the corrections depend on assumptions regarding the underlying data-generation model, suggesting that in high-dimensions it may be difficult to have universal, robust bootstrapping techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge