Interpretable Assessment of Fairness During Model Evaluation

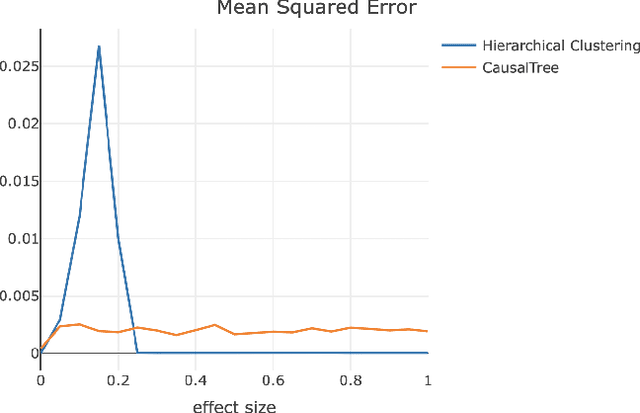
For companies developing products or algorithms, it is important to understand the potential effects not only globally, but also on sub-populations of users. In particular, it is important to detect if there are certain groups of users that are impacted differently compared to others with regard to business metrics or for whom a model treats unequally along fairness concerns. In this paper, we introduce a novel hierarchical clustering algorithm to detect heterogeneity among users in given sets of sub-populations with respect to any specified notion of group similarity. We prove statistical guarantees about the output and provide interpretable results. We demonstrate the performance of the algorithm on real data from LinkedIn.

Scalable Assessment and Mitigation Strategies for Fairness in Rankings

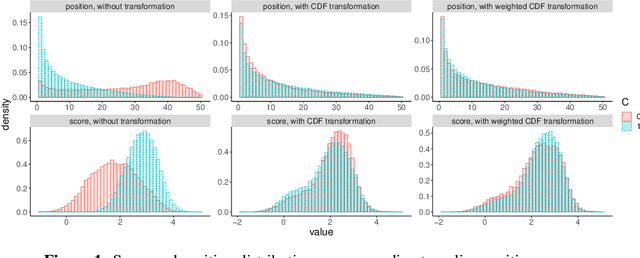
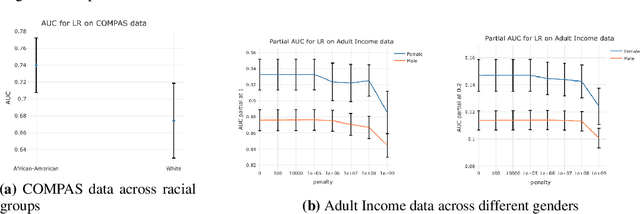
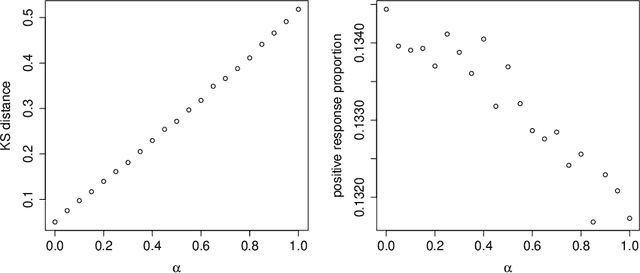
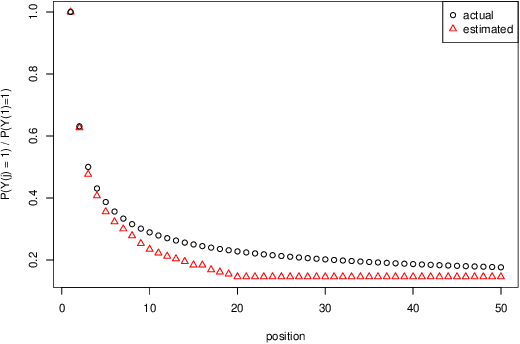
Motivated by industrial-scale applications, we consider two specific areas of fairness, one connected to the notion of equality of opportunity, and the other one generally tied to fair model performance. Throughout the paper, we consider only methods that can be scaled to Internet-industry size datasets. With this in mind, we propose a simple post-processing method to achieve equality of opportunity and discuss challenges and some solutions in the specific cases of recommendation systems and rankings. We then discuss a class of model performance fairness measures based on conditional ROC curves. We propose both scalable uncertainty assessment tools (that improve upon recent research) as well as scalable penalized methods to improve fairness with respect to these metrics. We provide fast algorithms with an emphasis on making few passes over the data when possible.

The Bayesian SLOPE

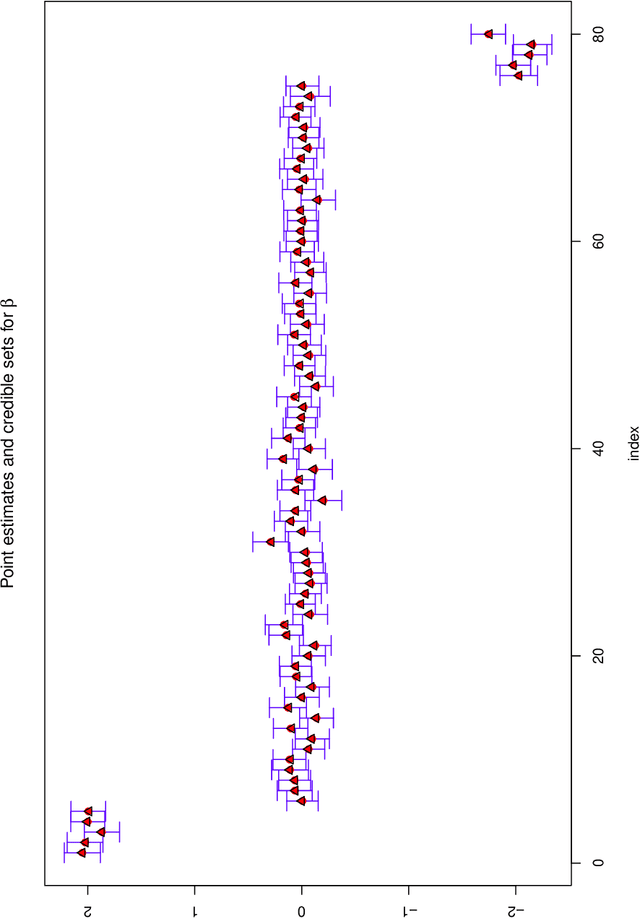
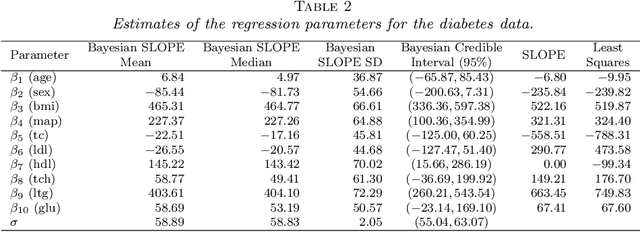
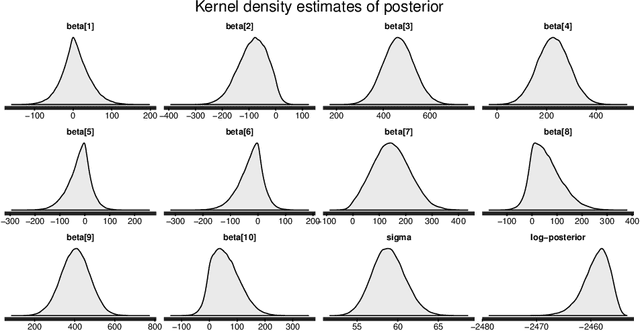
The SLOPE estimates regression coefficients by minimizing a regularized residual sum of squares using a sorted-$\ell_1$-norm penalty. The SLOPE combines testing and estimation in regression problems. It exhibits suitable variable selection and prediction properties, as well as minimax optimality. This paper introduces the Bayesian SLOPE procedure for linear regression. The classical SLOPE estimate is the posterior mode in the normal regression problem with an appropriate prior on the coefficients. The Bayesian SLOPE considers the full Bayesian model and has the advantage of offering credible sets and standard error estimates for the parameters. Moreover, the hierarchical Bayesian framework allows for full Bayesian and empirical Bayes treatment of the penalty coefficients; whereas it is not clear how to choose these coefficients when using the SLOPE on a general design matrix. A direct characterization of the posterior is provided which suggests a Gibbs sampler that does not involve latent variables. An efficient hybrid Gibbs sampler for the Bayesian SLOPE is introduced. Point estimation using the posterior mean is highlighted, which automatically facilitates the Bayesian prediction of future observations. These are demonstrated on real and synthetic data.