The Bayesian SLOPE

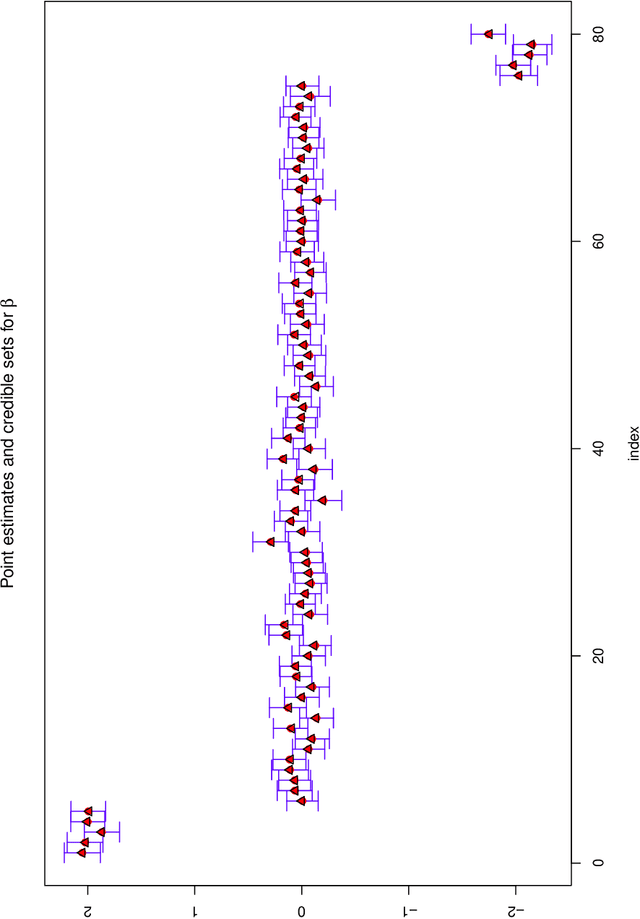
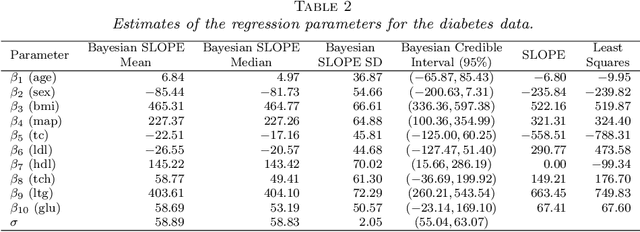
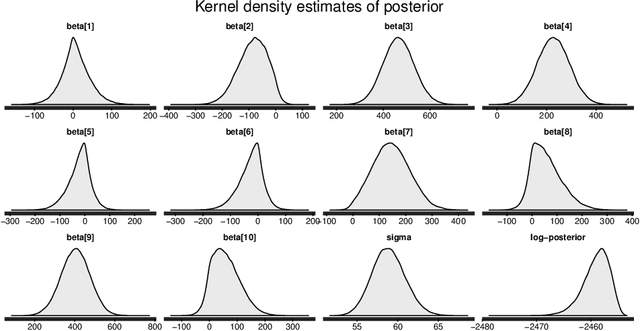
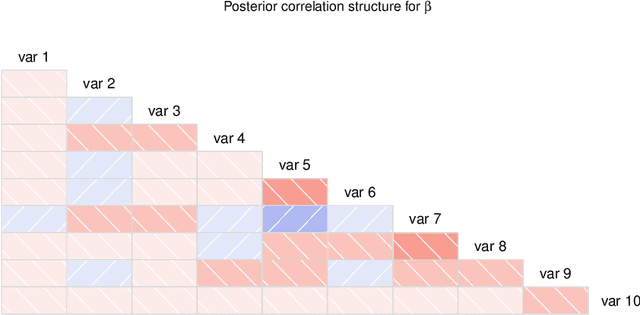
The SLOPE estimates regression coefficients by minimizing a regularized residual sum of squares using a sorted-$\ell_1$-norm penalty. The SLOPE combines testing and estimation in regression problems. It exhibits suitable variable selection and prediction properties, as well as minimax optimality. This paper introduces the Bayesian SLOPE procedure for linear regression. The classical SLOPE estimate is the posterior mode in the normal regression problem with an appropriate prior on the coefficients. The Bayesian SLOPE considers the full Bayesian model and has the advantage of offering credible sets and standard error estimates for the parameters. Moreover, the hierarchical Bayesian framework allows for full Bayesian and empirical Bayes treatment of the penalty coefficients; whereas it is not clear how to choose these coefficients when using the SLOPE on a general design matrix. A direct characterization of the posterior is provided which suggests a Gibbs sampler that does not involve latent variables. An efficient hybrid Gibbs sampler for the Bayesian SLOPE is introduced. Point estimation using the posterior mean is highlighted, which automatically facilitates the Bayesian prediction of future observations. These are demonstrated on real and synthetic data.